Chapitre 7 — Tests d’hypothèse
1 Introduction
Un test d’hypothèse est un procédé d’inférence permettant de contrôler (accepter ou rejeter) à partir de l’étude d’un ou plusieurs échantillons aléatoires, la validité d’hypothèses relatives à une ou plusieurs populations.
Les méthodes de l’inférence statistique nous permettent de déterminer, avec une probabilité donnée, si les différences constatées au niveau des échantillons peuvent être imputables au hasard ou si elles sont suffisamment importantes pour signifier que les échantillons proviennent de populations vraisemblablement différentes.
Les tests d’hypothèses font appel à un certain nombre d’hypothèses concernant la nature de la population dont provient l’échantillon étudié (normalité de la variable, égalité des variances, etc).
En fonction de l’hypothèse testée, plusieurs types de tests peuvent être réalisés :
- Les tests destinés à vérifier si un échantillon peut être considéré comme extrait d’une population donnée, vis-à-vis d’un paramètre comme la moyenne ou la fréquence observée (tests de conformité) ou par rapport à sa distribution observée (tests d’ajustement). Dans ce cas la loi théorique du paramètre est connue au niveau de la population.
Est-ce que le taux de glucose moyen mesuré dans un échantillon d’individus traités est conforme au taux de glucose moyen connu dans la population ? (test de conformité) Est-ce que la distribution des fréquences génotypiques observées pour un locus donné est conforme à celle attendue sous l’hypothèse du modèle de Hardy-Weinberg ? (test d’ajustement).
- Les tests destinés à comparer plusieurs populations à l’aide d’un nombre équivalent d’échantillons (tests d’égalité ou d’homogénéité) sont les plus couramment utilisés. Dans ce cas la loi théorique du paramètre est inconnue au niveau des populations.
On peut ajouter à cette catégorie le test d’indépendance qui cherche à tester l’indépendance entre deux caractères, généralement qualitatifs.
Y a-t-il une différence entre le taux de glucose moyen mesuré pour deux échantillons d’individus ayant reçu des traitements différents ? (tests d’égalité ou d’homogénéité). Est-ce que la distribution des fréquences génotypiques observées pour un locus donné est indépendante du sexe des individus ? (test d’indépendance).
2 Principe des tests
Le principe des tests d’hypothèse est de poser une hypothèse de travail et de prédire les conséquences de cette hypothèse pour la population ou l’échantillon. On compare ces prédictions avec les observations et l’on conclut en acceptant ou en rejetant l’hypothèse de travail à partir de règles de décisions objectives.
Définir les hypothèses de travail, constitue un élément essentiel des tests d’hypothèses de même que vérifier les conditions d’application de ces dernières (normalité de la variable, égalité des variances ou homoscédasticité, etc).
Différentes étapes doivent être suivies pour tester une hypothèse :
définir l’hypothèse nulle (notée \(H_0\)) à contrôler,
choisir un test statistique ou une statistique pour contrôler \(H_0\),
définir la distribution de la statistique sous l’hypothèse « \(H_0\) est réalisée »,
définir le niveau de signification du test ou région critique notée \(\alpha\),
calculer, à partir des données fournies par l’échantillon, la valeur de la statistique
prendre une décision concernant l’hypothèse posée et faire une interprétation biologique
2.1 Choix de l’hypothèse à tester
2.1.1 Hypothèse nulle et hypothèse alternative
L’hypothèse nulle notée \(H_0\) est l’hypothèse que l’on désire contrôler : elle consiste à dire qu’il n’existe pas de différence entre les paramètres comparés ou que la différence observée n’est pas significative et est due aux fluctuations d’échantillonnage.
Cette hypothèse est formulée dans le but d’être rejetée.
L’hypothèse alternative notée \(H_1\) est la négation de \(H_0\), elle est équivalente à dire « \(H_0\) est fausse ». La décision de rejeter \(H_0\) signifie que \(H_1\) est réalisée ou \(H_1\) est vraie.
Remarque : Il existe une dissymétrie importante dans les conclusions des tests. En effet, la décision d’accepter \(H_0\) n’est pas équivalente à « \(H_0\) est vraie et \(H_1\) est fausse ». Cela traduit seulement l’opinion selon laquelle, il n’y a pas d’évidence nette pour que \(H_0\) soit fausse.
Un test conduit à rejeter ou à ne pas rejeter une hypothèse nulle jamais à l’accepter d’emblée.
2.1.2 Test unilatéral ou bilatéral
La nature de \(H_0\) détermine la façon de formuler \(H_1\) et par conséquence la nature unilatérale ou bilatérale du test.
Test bilatéral
Si \(H_0\) consiste à dire que la population estudiantine avec une fréquence de fumeurs « \(p\) » est représentative de la population avec une fréquence de fumeurs « \(p_0\)», on pose alors :
\(H_0 : p = p_0\) et \(H_1 : p \neq p_0\)

Test unilatéral
Si l’on fait l’hypothèse que la fréquence de fumeurs dans la population estudiantine \(p\) est supérieure à la fréquence de fumeurs dans la population \(p\), on pose alors
\(H_0 : p = p_0\) et \(H_1 : p > p_0\)

Le raisonnement inverse peut être formulé avec l’hypothèse suivante :
\(H_0 : p = p_0\) et \(H_1 : p < p_0\)
Remarque : Seuls les tests bilatéraux seront développés dans le cours. Les tests unilatéraux seront traités au niveau des exemples.
2.2 Choix d’un test statistique
Ce choix dépend de la nature des données, du type d’hypothèse que l’on désire contrôler, des affirmations que l’on peut admettre concernant la nature des populations étudiées (normalité, égalité des variances) et d’autres critères que nous préciserons.
Un test statistique ou une statistique est une fonction des variables aléatoires représentant l’échantillon dont la valeur numérique obtenue pour l’échantillon considéré permet de distinguer entre \(H_0\) vraie et \(H_0\) fausse.
Dans la mesure où la loi de probabilité suivie par le paramètre \(p_0\) au niveau de la population en général est connue, on peut ainsi établir la loi de probabilité de la statistique \(S\) telle que :
\(S = p – p_0\) (voir intervalle de confiance d’une fréquence)
2.3 Choix de la région critique et règle de décision
Connaissant la loi de probabilité suivie par la statistique \(S\) sous l’hypothèse \(H_0\), il est possible d’établir une valeur seuil, \(S_{seuil}\) de la statistique pour une probabilité donnée appelée le niveau de signification du test : \(\alpha\).
La région critique correspond à l’ensemble des valeurs telles que
\(S > S_{seuil}\)
et le niveau de signification est telle que :
\(P ( S > S_{seuil} ) = \alpha\) avec \(P ( S \leq S_{seuil} ) = 1 - \alpha\)
Selon la nature unilatérale ou bilatérale du test, la définition de la région critique varie.

Il existe deux stratégies pour prendre une décision en ce qui concerne un test d’hypothèse :
la première stratégie fixe a priori la valeur du seuil de signification et la seconde établit la valeur de la probabilité critique \(\alpha_{obs}\) a posteriori.
Règles de décision 1 :
Sous l’hypothèse « \(H_0\) est vraie » et pour un seuil de signification \(\alpha\) fixé
- si la valeur de la statistique \(S\) calculée (\(S_{obs}\)) est supérieure à la valeur seuil (\(S_{seuil}\))
\(S_{obs} > S_{seuil}\) alors l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) et l’hypothèse \(H_1\) est acceptée.
- si la valeur de la statistique \(S\) calculée (\(S_{obs}\)) est inférieure à la valeur seuil \(S_{seuil}\)
\(S_{obs} \leq S_{seuil}\) alors l’hypothèse \(H_0\) ne peut être rejetée.
Remarque : Le choix du risque a est lié aux conséquences pratiques de la décision : si les conséquences sont graves, on choisira \(\alpha = 1\%\) ou \(1‰\), mais si le débat est plutôt académique, le traditionnel \(\alpha = 5%\) fera le plus souvent l’affaire.
Règles de décision 2 :
La probabilité critique \(\alpha\) telle que \(P(S \geq S_{obs}) = a_{obs}\) est évaluée
si \(a_{obs} = 0,05\) l’hypothèse \(H_0\) est acceptée car le risque d’erreur de rejeter \(H_0\) alors qu’elle est vrai est trop important.
si \(a_{obs} < 0,05\) l’hypothèse \(H_0\) est rejetée car le risque d’erreur de rejeter \(H_0\) alors qu’elle est vrai est très faible.
2.4 Risques d’erreur, puissance et robustesse d’un test
2.4.1 Risque d’erreur de première espèce \(\alpha\)
Le risque d’erreur \(\alpha\) est la probabilité que la valeur expérimentale ou calculée de la statistique \(S\) appartienne à la région critique si \(H_0\) est vrai. Dans ce cas \(H_0\) est rejetée et \(H_1\) est considérée comme vraie.
Le risque \(\alpha\) de première espèce est celui de rejeter \(H_0\) alors qu’elle est vraie
\(\alpha = P( \ \text{rejeter}\ H_0 / H_0 \ \text{vrai}\ )\)
ou accepter \(H_1\) alors qu’elle est fausse
\(\alpha = P( \ \text{accepter} H_1 / H_1 \ \text{fausse})\)
La valeur du risque \(\alpha\) doit être fixée a priori par l’expérimentateur et jamais en fonction des données. C’est un compromis entre le risque de conclure à tort et la faculté de conclure.
Remarque : Toutes choses étant égales par ailleurs, la région critique diminue lorsque \(\alpha\) décroît (voir intervalle de confiance) et donc on rejette moins fréquemment \(H_0\). A vouloir commettre moins d’erreurs, on conclut plus rarement.
Exemple :
Si l’on cherche à tester l’hypothèse qu’une pièce de monnaie n’est pas « truquée », nous allons adopter la régle de décision suivante :
\(H_0\) : la pièce n’est pas truquée est
acceptée si \(X \in [40,60]\)
rejetée si \(X \notin [40,60]\) donc soit \(X < 40\) ou \(X > 60\)
avec \(X\) « nombre de faces » obtenus en lançant 100 fois la pièce.
Quel est **le risque d’erreur de première espèce \(\alpha\)* dans ce cas ? Réponse.
2.4.2 Risque d’erreur de deuxième espèce \(\beta\)
Le risque d’erreur \(\beta\) est la probabilité que la valeur expérimentale ou calculée de la statistique n’appartienne pas à la région critique si \(H_1\) est vrai. Dans ce cas \(H_0\) est acceptée et \(H_1\) est considérée comme fausse.
Le risque \(\beta\) de deuxième espèce est celui d’accepter \(H_0\) alors qu’elle est fausse =
\(\beta = P(\ \text{accepter}\ H_0 / H_0\ \text{fausse}\ )\) ou \(P(\ \text{accepter}\ H_0 / H_1 \ \text{vrai}\ )\)
ou rejeter \(H_1\) alors qu’elle est vraie
\(\beta = P( \ \text{rejeter}\ H_1 / H_1 \ \text{vrai}\ )\)
Remarque : Pour quantifier le risque \(\beta\), il faut connaître la loi de probabilité de la statistique \(S\) sous l’hypothèse \(H_1\).
Exemple :
Si l’on reprend l’exemple précédent de la pièce de monnaie, la probabilité \(p\) d’obtenir face est de 0,6 pour une pièce truquée. Si l’on adopte toujours la même régle de décision :
\(H_0\) : la pièce n’est pas truquée est
- acceptée si \(X \in [40,60]\)
- rejetée si \(X \notin [40,60]\) donc soit \(X < 40\) ou \(X > 60\)
avec \(X\) « nombre de faces » obtenues en lançant 100 fois la pièce.
Quel est le **risque d’erreur de second espèce \(\beta\) dans ce cas ? Réponse.
2.4.3 La puissance et la robustesse d’un test \((1 - \beta)\)
Les tests ne sont pas faits pour « démontrer » \(H_0\) mais pour « rejeter » \(H_0\) . L’aptitude d’un test à rejeter \(H_0\) alors qu’elle est fausse constitue la puissance du test.
La puissance d’un test est : \(1 - \beta = P(\ \text{rejeter}\ H_0 / H_0\ \text{fausse}\ ) = P(\ \text{accepter}\ H_1/H_1 \ \text{vraie}\ )\)
La relation entre les deux risques d’erreur figure sur le graphe ci-dessous.
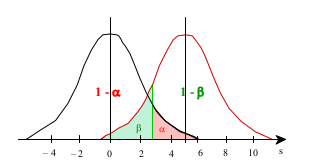
La puissance d’un test est fonction de la nature de \(H_1\), un test unilatéral est plus puissant qu’un test bilatéral.
La puissance d’un test augmente avec taille de l’échantillon \(N\) étudié à valeur de a constant.
La puissance d’un test diminue lorsque \(\alpha\) diminue.
Exemple :
Si l’on reprend l’exemple précédent de la pièce de monnaie, calculez la puissance du test lorsque la probabilité d’obtenir face est respectivement 0,3 - 0,4 - 0,6 - 0,7 -0,8 pour une pièce truquée. Que constatez-vous ? Réponse.
Les différentes situations que l’on peut rencontrer dans le cadre des tests d’hypothèse sont résumées dans le tableau suivant :

La robustesse d’une technique statistique représente sa sensibilité à des écarts aux hypothèses faites.
Exemple : Toute chose étant égale par ailleurs, que se passe-t-il si l’hypothèse de normalité n’est pas satisfaite ?
3 Tests de conformité
Les tests de conformité sont destinés à vérifier si un échantillon peut être considéré comme extrait d’une population donnée ou représentatif de cette population, vis-à-vis d’un paramètre comme la moyenne, la variance ou la fréquence observée. Ceci implique que la loi théorique du paramètre est connue au niveau de la population.
3.1 Comparaison d’une moyenne observée et d’une moyenne théorique
3.1.1 Principe du test
Soit \(X\), une variable aléatoire observée sur une population, suivant une loi normale et un échantillon extrait de cette population.
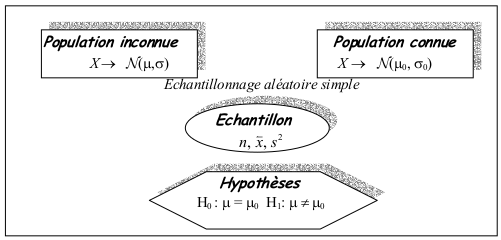
Le but est de savoir si un échantillon de moyenne \(\bar{x}\), estimateur de \(\mu\), appartient à une population de référence connue d’espérance \(\mu_0\) (\(H_0\) vraie) et ne diffère de \(\mu_0\) que par des fluctuations d’échantillonnage ou bien appartient à une autre population inconnue d’espérance \(\mu\) (\(H_1\) vraie).
Pour tester cette hypothèse, il existe deux statistiques : la variance \(\sigma_0^2\) de la population de référence est connue (test \(\varepsilon\)) ou cette variance est inconnue et il faut l’estimer (test T).
3.1.2 Variance de la population connue
3.1.2.1 Statistique du test
Soit \(\overset{\leftharpoonup}{X}\) la distribution d’échantillonnage de la moyenne dans la population inconnue suit une loi normale telle que : \(\overset{\leftharpoonup}{X} \rightarrow \mathcal{N} (\mu, \sqrt {\frac{\sigma^2}{n}})\).
La statistique étudiée est l’écart : \(S = \bar{X} - \mu_0\) dont la distribution de probabilité est la suivante
\(S \rightarrow \mathcal{N} (0, \sqrt {\frac{\sigma^2}{n}})\) avec sous \(H_0\), \(E(S) = 0\) et \(V(S) = \frac{\sigma^2}{n}\) (voir démonstration)
Nous pouvons établir grâce au théorème central limite la variable Z centrée réduite telle que
\(Z = \frac{S - E(S)}{\sqrt {V(S)} }= \frac{\bar{X} - {\mu_0} } { \sqrt {\frac{\sigma^2}{n} } }\)
Sous \(H_0 : \mu = \mu_0\) avec \(\sigma^2\) connue
\(Z = \frac{\bar{X} - {\mu_0} } {\sqrt { \frac{\sigma^2}{n} } }\) suit une loi normale centrée réduite \(\mathcal{N}(0,1)\).
3.1.2.2 Application et Décision
L’hypothèse testée est la suivante :
\(H_0 : \mu = \mu_0\) contre \(H_1 : \mu \neq \mu_0\)
Une valeur \(z\) de la variable aléatoire \(Z\) est calculée :
\(z = \frac{ | \overset{\leftharpoonup}{x} - {\mu_0} | } { \sqrt {\frac{\sigma^2}{n}} }\) notée aussi \(\varepsilon_{obs}\)
\(\varepsilon\) calculée ({obs}) est comparée avec la valeur {seuil} lue sur la table de la loi normale centrée réduite pour un risque d’erreur \(\alpha\) fixé (Règle de décision 1).
si \(\varepsilon_{obs} > \varepsilon_{seuil}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : l’échantillon appartient à une population d’espérance \(\mu\) et n’est pas représentatif de la population de référance d’espérance \(\mu_0\).
si \(\varepsilon_{obs} \leq \varepsilon_{seuil}\) l’hypothèse \(H_0\) est acceptée: l’échantillon est représentatif de la population de référence d’espérance \(\mu_0\).
Exemple :
La glycémie d’une population suit une loi normale d’espérance \(\mu_0\) = 1g/l et d’écart-type \(\sigma_0\) = 0,1 g/l.
On relève les glycémies chez 9 patients. On trouve \(\bar{x}\) = 1,12g/l.
Cet échantillon est-il représentatif de la population ? Réponse.
3.1.3 Variance de la population inconnue
3.1.3.1 Statistique du test
La démarche est la même que pour le test \(\varepsilon\) mais la variance de la population n’étant pas connue, elle est estimée par :
\({\hat \sigma ^2} = \frac{n}{n - 1} s^2\) (voir estimation ponctuelle)
La statistique étudiée est l’écart : \(S = \bar{X} - \mu_0\) dont la distribution de probabilité est la suivante
S (0, \(\sqrt {\frac{{\hat \sigma }^2}{n}})\) avec \(E(S) = 0\) et \(V(S) = \frac{{\hat \sigma}^2}{n}\) (voir démonstration)
Nous pouvons établir grâce au théorème central limite la variable T centrée réduite telle que
\(T = \frac { S - E(S) }{ \sqrt{V(S) } } = \frac{ \bar{X} - {\mu_0} } { \sqrt{\frac{\hat {\sigma}^2}{n} }}\)
Sous \(H_0 : \mu = \mu_0\) avec \(\sigma^2\) inconnue
\(T = \frac{{\bar{X}- {\mu_0}}}{{\sqrt {\frac{{{{\hat \sigma }^2}}}{n}} }}\) suit une une loi de Student à \(n-1\) degrés de liberté.
3.1.3.2 Application et Décision
L’hypothèse testée est la suivante :
\(H_0 : \mu = \mu_0\) contre \(H_1 : \mu \neq \mu_0\)
Une valeur \(t\) de la variable aléatoire \(T\) est calculée :
\(t = \frac{{\left| {\bar{x}- {\mu_0}} \right|}}{{\sqrt {\frac{{{{\hat \sigma }^2}}}{n}} }} = \frac{{\left| {\bar{x}- {\mu_0}} \right|}}{{\sqrt {\frac{{{s^2}}}{{n - 1}}} }}\)
\(t\) calculée (\(t_{obs}\)) est comparée avec la valeur \(t_{seuil}\) lue dans la table de Student pour un risque d’erreur \(\alpha\) fixé et (\(n - 1\)) degrés de liberté.
si \(t_{obs} > t_{seuil}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : l’échantillon appartient à une population d’espérance \(\mu\) et n’est pas représentatif de la population de référence d’espérance \(\mu_0\).
si \(t_{obs} \leq t_{seuil}\) l’hypothèse \(H_0\) est acceptée: l’échantillon est représentatif de la population de référence d’espérance \(\mu_0\).
Remarque:
Si \(n < 30\), la variable aléatoire \(X\) étudiée doit impérativement suivre une loi normale \(\mathcal{N}(\mu,\sigma)\). Pour \(n \neq 30\), la variable de student \(t\) converge vers une loi normale centrée réduite \(\varepsilon\).
Exemple :
Pour étudier un lot de fabrication de comprimés, on prélève au hasard 10 comprimés parmis les 30 000 produits et on les pèse. On observe les valeurs de poids en grammes :
0,81 – 0,84 – 0,83 – 0,80 – 0,85 – 0,86 – 0,85 – 0,83 – 0,84 – 0,80
Le poids moyen observé est-il compatible avec la valeur 0,83g, moyenne de la production au seuil 98% ? Réponse.
3.2 Comparaison d’une fréquence observée et d’une fréquence théorique
3.2.1 Principe du test
Soit \(X\) une variable qualitative prenant deux modalités (succès \(X=1\), échec \(X=0\)) observée sur une population et un échantillon extrait de cette population.

Le but est de savoir si un échantillon de fréquence observée \(\frac{K}{n}\), estimateur de \(p\), appartient à une population de référence connue de fréquence \(p_0\) (\(H_0\) vraie) ou à une autre population inconnue de fréquence \(p\) (\(H_1\) vraie).
3.2.2 Statistique du test
La distribution d’échantillonnage de la fréquence de succès dans la population inconnue, \(\frac{K}{n}\) suit une loi normale telle que : \(\frac{K}{n}\) suit \(\mathcal{N}(p, \sqrt { \frac{p_0 q_0}{n} } )\), les variances étant supposées égales dans la population de référence et la population d’où est extrait l’échantillon.
La statistique étudiée est l’écart : \(S = \frac{K}{n} – p_0\) dont la distribution de probabilité est la suivante \(S \rightarrow \mathcal{N} (0, \sqrt{ \frac{p_0 q_0}{n} } )\) avec sous \(H_0\) \(E(S) = 0\) et \(V(S) = \frac{p_0 q_0}{n}\) (voir démonstration)
Nous pouvons établir grâce au théorème central limite la variable \(Z\) centrée réduite telle que
\(Z = \frac{S - E(S)}{\sqrt {V(S)}} = \frac{ \frac{K}{n} - {p_0} }{\sqrt {\frac{p_0 q_0}{n}} }\) mais seulement si \(n p_0\) et \(n q_0\) \(\geq 10\)
Sous \(H_0 : p = p_0\)
\(Z = \frac{{\frac{K}{n} - {p_0}}}{{\sqrt {\frac{{{p_0}{q_0}}}{n}} }}\) suit une loi normale centrée réduite \(\mathcal{N}(0,1)\).
3.2.3 Application et décision
L’hypothèse testée est la suivante :
\(H_0 : p = p_0\) contre \(H_1 : p \neq p_0\)
Une valeur \(z\) de la variable aléatoire \(Z\) est calculée :
\(z = \frac{{\left| {\frac{k}{n} - {p_0}} \right|}}{{\sqrt {\frac{{{p_0}{q_0}}}{n}} }}\) notée aussi \(\varepsilon_{obs}\)
\(\varepsilon\) calculée (\(\varepsilon_{obs}\)) est comparée avec la valeur \(\varepsilon_{seuil}\) lue sur la table de la loi normale centrée réduite pour un risque d’erreur \(\alpha\) fixé (Règles de décision 1).
si \(\varepsilon_{obs} > \varepsilon_{seuil}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : l’échantillon appartient à une population de fréquence \(p\) et n’est pas représentatif de la population de référence de fréquence \(p_0\) .
si \(\varepsilon_{obs} \leq \varepsilon_{seuil}\) l’hypothèse \(H_0\) est acceptée: l’échantillon est représentatif de la population de référence de fréquence \(p_0\).
Exemple :
Une anomalie génétique touche en France 1/1000 des individus. On a constaté dans une région donnée : 57 personnes atteintes sur 50 000 naissances.
Cette région est-elle représentative de la France entière ? Réponse.
4 Tests d’homogénéité
Les tests d’homogénéité destinés à comparer deux populations à l’aide d’un nombre équivalent d’échantillons (tests d’égalité ou d’homogénéité) sont les plus couramment utilisés. Dans ce cas la loi théorique du paramètre étudié (par exemple \(p\), \(\mu\) , \(\sigma^2\) ) est inconnue au niveau des populations étudiées.
4.1 Comparaison de deux variances
4.1.1 Principe du test
Soit \(X\), une variable aléatoire observée sur 2 populations suivant une loi normale et deux échantillons indépendants extraits de ces deux populations.
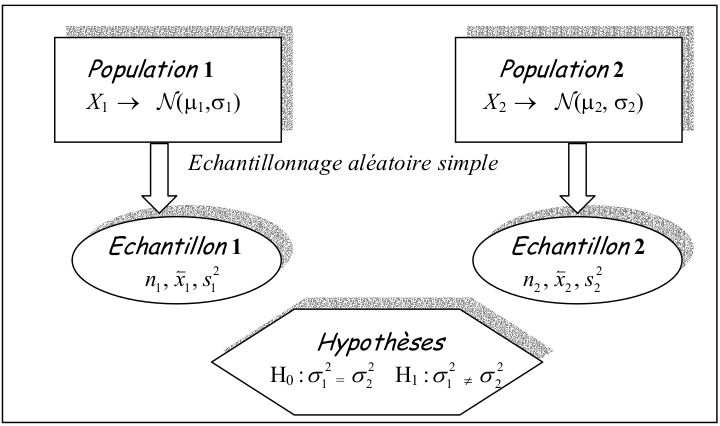
On fait l’hypothèse que les deux échantillons proviennent de 2 populations dont les variances sont égales.
Le test de comparaison de variance est nécessaire lors de la comparaison de deux moyennes lorsque les variances des populations \(\sigma_1^2\)et \(\sigma_2^2\) ne sont pas connues. C’est également la statistique associée à l’analyse de variance.
4.1.2 Statistique du test
La statistique associée au test de comparaison de deux variances correspond au rapport des deux variances estimées.
Sous \(H_0 : \sigma_1^2 = \sigma_2^2\)
\({F_{obs.}} = \frac{{\hat \sigma_1^2}}{{\hat \sigma_2^2}} = \frac{{\frac{{{n_1}}}{{n_1 - 1}}s_1^2}}{{\frac{{{n_2}}}{{{n_2} - 1}}s_2^2}}\) suit une loi de Fisher-Snedecor à (\(n_1-1\), \(n_2 -1\)) degrés de liberté
avec \(\hat \sigma_1^2 > \hat \sigma_2^2\) car le rapport des variances doit être supérieur à 1.
Remarque : Il existe d’autres statistiques que celle de Fisher –Snédecor pour comparer deux variances, notamment le test de Hartley qui impose l’égalité de la taille des échantillons comparés \(n_1 = n_2\) mais que nous ne développerons pas dans ce cours.
4.1.3 Application et décision
La valeur de la statistique \(F\) calculée (\({F_{obs.}}\)) est comparée avec la valeur \({F_{seuil}}\) lue dans la table de la loi de Fisher-Snedecor pour un risque d’erreur \(\alpha\) fixé et (\(n_1-1\), \(n_2 -1\)) degrés de liberté.
si \({F_{obs.}} \geq {F_{seuil}}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : les deux échantillons sont extraits de deux populations ayant des variances statistiquement différentes \(\sigma_1^2\) et \(\sigma_2^2\).
si \({F_{obs.}} \leq {F_{seuil}}\) l’hypothèse \(H_0\) est acceptée: les deux échantillons sont extraits de deux populations ayant même variance \(\sigma^2\).
Remarque : Pour l’application de ce test, il est impératif que \(X \rightarrow \mathcal{N}(\mu,\sigma)\) et que les deux échantillons soient indépendants.
Exemple :
Un biologiste effectue des dosages par une méthode de mesure de radioactivité et ne dispose donc que d’un nombre très limité de valeurs.
Les concentrations \(C_1\) et \(C_2\) mesurées sur deux prélèvements ont donné les valeurs suivantes :
\(C_1\) : 3,9 – 3,8 – 4,1 – 3,6 \(C_2\) : 3,9 – 2,8 – 3,1 – 3,7 – 4,1
La variabilité des valeurs obtenues pour les deux prélèvements est-elle similaire ? Réponse.
4.2 Comparaison de deux moyennes
4.2.1 Principe du test
Soit \(X\) un caractère quantitatif continu observé sur 2 populations suivant une loi normale et deux échantillons indépendants extraits de ces deux populations.

On fait l’hypothèse que les deux échantillons proviennent de 2 populations dont les espérances sont égales.
Il existe plusieurs statistiques associées à la comparaison de deux moyennes en fonction de la nature des données.

4.2.2 Les variances des populations sont connues
4.2.2.1 Statistique du test
Soit \(\overset{\leftharpoonup}{X_1}\) la distribution d’échantillonnage de la moyenne dans la population 1 suit une loi normale telle que : \(\overset{\leftharpoonup}{X_1} \rightarrow \mathcal{N} (\mu_1, \frac{\sigma_1^2}{n_1})\) et de même pour \(\overset{\leftharpoonup}{X_2} \rightarrow \mathcal{N} (\mu_2, \frac{\sigma_2^2}{n_2})\)
\(\overset{\leftharpoonup}{X_1}\) et \(\overset{\leftharpoonup}{X_2}\) étant deux variables aléatoires indépendantes, nous pouvons établir la loi de probabilité de la variable aléatoire à étudier \(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}\)
\(E(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}) = E(\overset{\leftharpoonup}{X_1}) - E(\overset{\leftharpoonup}{X_2}) = \mu_1 - \mu_2\) (Propriété de l’ espérance)
\(V(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}) = V(\overset{\leftharpoonup}{X_1}) - V(\overset{\leftharpoonup}{X_2}) = \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\) (Propriété de la variance)
- Sachant que \(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}\) suit une loi normale \(\mathcal{N}(\mu_1 - \mu_2 , \sqrt {\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} )\) , nous pouvons établir grâce au théorème central limite la variable \(Z\) centrée réduite telle que
\(Z = \frac{ ( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} ) - E( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} ) }{ \sqrt{ V(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}) } } = \frac{ ( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} ) - ({\mu_1} - {\mu_2}) }{ \sqrt {\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} }\)
Sous \(H_0 : \mu_1 = \mu_2\) avec \(\sigma_1^2\) et \(\sigma_2^2\) connues
\(Z = \frac{ ( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} ) }{ \sqrt {\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}} }\) suit une loi normale centrée réduite \(\mathcal{N}(0,1)\).
4.2.2.2 Application et décision
L’hypothèse testée est la suivante :
\(H_0 : \mu_1 = \mu_2\) contre \(H_1 : \mu_1 \neq \mu_2\)
Une valeur \(z\) de la variable aléatoire \(Z\) est calculée :
\(z = \frac{{\left| {\overset{\leftharpoonup}{x_1} - \overset{\leftharpoonup}{x_2}} \right|}}{{\sqrt {\frac{{\sigma_1^2}}{{{n_1}}} + \frac{{\sigma_2^2}}{{{n_2}}}} }}\) notée aussi \(\varepsilon_{obs}\)
\(\varepsilon\) calculée (\(\varepsilon_{obs}\)) est comparée avec la valeur \(\varepsilon_{seuil}\) lue sur la table de la loi normale centrée réduite pour un risque d’erreur \(\alpha\) fixé.
si \(\varepsilon_{obs} \geq \varepsilon_{seuil}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : les deux échantillons sont extraits de deux populations ayant des espérances respectivement \(\mu_1\) et \(\mu_2\).
si \(\varepsilon_{obs} \leq \varepsilon_{seuil}\) l’hypothèse \(H_0\) est acceptée: les deux échantillons sont extraits de deux populations ayant même espérance \(\mu\).
Remarque : Pour l’application de ce test, il est impératif que \(X \rightarrow \mathcal{N}(\mu,\sigma)\) pour les échantillons de taille < 30 et que les deux échantillons soient indépendants.
Exemple :
On a effectué une étude, en milieu urbain et en milieu rural, sur le rythme cardiaque humain :

Peut-on affirmer qu’il existe une différence significative entre les rythmes cardiaques moyens des deux populations ? Réponse.
4.2.3 Les variances des populations sont inconnues et égales
4.2.3.1 Statistique du test
- Les variances des populations n’étant pas connues, on fait l’hypothèse que les deux populations présentent la même variance.
\(H_0 : \sigma_1^2 = \sigma_2^2 = \sigma^2\) (voir test de comparaison des variances)
- L’égalité des variances des deux populations ou homoscédasticité permet alors d’établir la loi de probabilité de \(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}\) avec
\(\overset{\leftharpoonup}{X_1} \rightarrow \mathcal{N} (\mu_1, \frac{\sigma ^2}{n_1})\) et \(\overset{\leftharpoonup}{X_2} \rightarrow \mathcal{N} (\mu_1, \frac{\sigma ^2}{n_2})\)
- Sachant que \(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}\) suit une loi normale \(\mathcal{N}(\mu_1 - \mu_2 , \sqrt {{\sigma ^2}\left( {\frac{1}{n_1} + \frac{1}{n_2}} \right)})\), nous pouvons établir grâce au théorème central limite la variable \(T\) telle que
\(T = \frac{ ( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} ) - E( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} ) }{ \sqrt{ V(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}) } } = \frac{ ( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} ) - ({\mu_1} - {\mu_2}) }{ \sqrt {{\sigma ^2}\left( {\frac{1}{n_1} + \frac{1}{n_2}} \right)} }\)
Sous \(H_0 : \mu_1 = \mu_2\) avec \(\sigma_1^2 = \sigma_2^2 = \sigma^2\)
\(T = \frac{( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} )}{{\sqrt {{\sigma ^2}\left( {\frac{1}{{{n_1}}} + \frac{1}{{{n_2}}}} \right)} }}\) suit une loi de Student à (\(n_1 + n_2 - 2\)) degrés de liberté
4.2.3.2 Application et décision
L’hypothèse testée est la suivante :
\(H_0 : \mu_1 = \mu_2\) contre \(H_1 : \mu_1 \neq \mu_2\)
Les variances des populations n’étant pas connues, l’égalité des variances doit être vérifiée
\(H_0 :\sigma_1^2 = \sigma_2^2 = \sigma^2\) contre \(H_1 : \sigma_1^2 \neq \sigma_2^2\) test de Fisher-Snedecor.
Une valeur \(t\) de la variable aléatoire \(T\) est calculée :
\(t = \frac{{\left| {\overset{\leftharpoonup}{x_1} - \overset{\leftharpoonup}{x_2}} \right|}}{{\sqrt {{{\hat \sigma }^2}\left( {\frac{1}{{{n_1}}} + \frac{1}{{{n_2}}}} \right)} }}\) avec \({\hat \sigma ^2} = \frac{{{n_1}s_1^2 + {n_2}s_2^2}}{{{n_1} + {n_2} - 2}}\) estimation de la variance \(\sigma^2\) commune
\(t\) calculée (\(t_{obs}\)) est comparée avec la valeur \(t_{seuil}\) lue dans la table de Student pour un risque d’erreur \(\alpha\) fixé et (\(n_1 + n_2 – 2\)) degrés de liberté.
si \(t_{obs} > t_{seuil}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : les deux échantillons sont extraits de deux populations ayant des espérances respectivement \(\mu_1\) et \(\mu_2\).
si \(t_{obs} \leq t_{seuil}\) l’hypothèse \(H_0\) est acceptée: les deux échantillons sont extraits de deux populations ayant même espérance \(\mu\).
Remarque : Pour l’application de ce test, il est impératif que \(X \rightarrow \mathcal{N}(\mu,\sigma)\) pour les échantillons de taille < 30, que les deux échantillons soient indépendants et que les deux variances estimées soient égales.
Exemple :
Dans le but d’étudier l’influence du type d’atmosphère d’élevage sur la durée de développement des drosophiles femelles, ces dernières ont été élevées à 14°C sous atmosphère normale (N) ou enrichie en C02 (C02). Les résultats suivants ont été obtenus :

Que peut-on conclure ? Réponse.
4.2.4 Les variances des populations sont inconnues et inégales
Si les variances des populations ne sont pas connues et si leurs estimations à partir des échantillons sont significativement différentes ( test de comparaison des variances), il faut considérer deux cas de figure selon la taille des échantillons comparés :
les grands échantillons avec \(n_1\) et \(n_2\) supérieurs à 30.
les petits échantillons avec \(n_1\) et/ou \(n_2\) inférieurs à 30.
Cas où \(n_1\) et \(n_2\) > 30
La statistique utilisée est la même que pour le cas où les variances sont connues.
Sous \(H_0 : \mu_1 = \mu_2\)
\(Z = \frac{( \overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2} )}{{\sqrt {\frac{{\sigma_1^2}}{{{n_1}}} + \frac{{\sigma_2^2}}{{{n_2}}}} }}\) suit une loi normale centrée réduite \(\mathcal{N}(0,1)\).
Comme les variances sont inconnues et significativement différentes \(\sigma_1^2 \neq \sigma_2^2\), on remplace les variances des populations par leurs estimations ponctuelles calculées à partir des échantillons, \(\hat \sigma_1^2 = \frac{n_1}{{n_1} - 1}s_1^2\) et \(\hat \sigma_2^2 = \frac{n_2}{{n_2} - 1}s_2^2\)
L’hypothèse testée est la suivante :
\(H_0 : \mu_1 = \mu_2\) contre \(H_1 : \mu_1 \neq \mu_2\)
Une valeur \(z\) de la variable aléatoire \(Z\) est calculée :
\(z = \frac{{\left| {\overset{\leftharpoonup}{x_1} - \overset{\leftharpoonup}{x_2}} \right|}}{{\sqrt {\frac{{\hat \sigma_1^2}}{{{n_1}}} + \frac{{\hat \sigma_2^2}}{{{n_2}}}} }} = \frac{{\left| {\overset{\leftharpoonup}{x_1} - \overset{\leftharpoonup}{x_2}} \right|}}{{\sqrt {\frac{{s_1^2}}{{{n_1} - 1}} + \frac{{s_2^2}}{{{n_2} - 1}}} }} = \varepsilon_{obs}\)
\(\varepsilon\) calculée (\(\varepsilon_{obs}\)) est comparée avec la valeur \(\varepsilon_{seuil}\) lue sur la table de la loi normale centrée réduite pour un risque d’erreur \(\alpha\) fixé.
si \(\varepsilon_{obs} > \varepsilon_{seuil}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : les deux échantillons sont extraits de deux populations ayant des espérances respectivement \(\mu_1\) et \(\mu_2\).
si \(\varepsilon_{obs} \leq \varepsilon_{seuil}\) l’hypothèse \(H_0\) est acceptée: les deux échantillons sont extraits de deux populations ayant même espérance \(\mu\).
Remarque : Pour l’application de ce test, il est impératif que \(X \rightarrow \mathcal{N}(\mu,\sigma)\) et que les deux échantillons soient indépendants.
Exemple :
Dans le but d’étudier l’influence éventuelle de la lumière sur la croissance du poisson Lebistes Reticulus, on a élevé deux lots de ce poisson dans des conditions d’éclairage différentes. Au 95ème jour, on a mesuré en mm les longueurs \(x_i\) des poissons. On a obtenu les résultats suivants :
Lot 1 (180 individus) : éclairage à 400 lux \(\sum {{x_{i1}}}= 3 780 \qquad \sum {x_{i1}^2} = 84 884\)
Lot 2 (90 individus) : éclairage à 3 000 lux. \(\sum {{x_{i2}}}= 2 043 \qquad \sum {x_{i2}^2} = 46 586\)
Que peut-on conclure ? Réponse.
Cas où \(n_1\) et/ou \(n_2\) < 30
Lorsque les variances sont inégales et les échantillons de petites tailles, la loi de probabilité suivie par \(\overset{\leftharpoonup}{X_1} - \overset{\leftharpoonup}{X_2}\) n’est pas connue. On a recours alors au statistique non paramétrique.
4.3 Comparaison de deux fréquences
4.3.1 Principe du test
Soit \(X\) une variable qualitative prenant deux modalités (succès \(X=1\), échec \(X=0\)) observée sur 2 populations et deux échantillons indépendants extraits de ces deux populations. On fait l’hypothèse que les deux échantillons proviennent de 2 populations dont les probabilités de succès sont identiques.

Le problème est de savoir si la différence entre les deux fréquences observées est réelle ou explicable par les fluctuations d’échantillonnage. Pour résoudre ce problème, deux tests de comparaison de fréquences sont possibles :
Test \(\varepsilon\) ou test de la variable centrée réduite et test du Khi-deux \(\chi^2\)
4.3.2 Statistique du test \(\varepsilon\)
- La distribution d’échantillonnage de la fréquence de succès dans la population 1, \(\frac{K_1}{n_1}\) suit une loi normale telle que :
\(\frac{K_1}{n_1}\) suit \(\mathcal{N} (p_1, \sqrt {\frac{{p_1}{q_1}}{n_1}})\) et de même pour \(\frac{K_2}{n_2}\) suit \(\mathcal{N} (p_2, \sqrt {\frac{{p_2}{q_2}}{n_2}} )\)
si et seulement si \(n_1 p_1, n_1 q_1, n_2 p_2, n_2 q_2 \geq 10\)
- \(\frac{K_1}{n_1}\) et \(\frac{K_2}{n_2}\) étant deux variables aléatoires indépendantes, nous pouvons établir la loi de probabilité de la variable aléatoire à étudier \(\frac{K_1}{n_1} - \frac{K_2}{n_2}\)
\(E(\frac{K_1}{n_1} - \frac{K_2}{n_2}) = E(\frac{K_1}{n_1}) - E(\frac{K_2}{n_2}) = p_1 - p_2\) (Propriété de l’ espérance)
\(V(\frac{K_1}{n_1} - \frac{K_2}{n_2}) = V(\frac{K_1}{n_1}) + V(\frac{K_2}{n_2}) = \frac{{p_1}{q_1}}{n_1} + \frac{{p_2}{q_2}}{n_2}\) (Propriété de la variance)
- Sachant que \(\frac{K_1}{n_1} - \frac{K_2}{n_2}\) suit une loi normale \(\mathcal{N}(p_1 - p_2 , \sqrt {\frac{{p_1}{q_1}}{n_1} + \frac{{p_2}{q_2}}{n_2}} )\), nous pouvons établir grâce au théorème central limite la variable \(Z\) centrée réduite telle que
\(Z = \frac{{\left( {\frac{{{K_1}}}{{{n_1}}} - \frac{{{K_2}}}{{{n_2}}}} \right) - \left( {{p_1} - {p_2}} \right)}}{{\sqrt {\frac{{{p_1}{q_1}}}{{{n_1}}} + \frac{{{p_2}{q_2}}}{{{n_2}}}} }}\)
Sous \(H_0 : p_1 = p_2\) avec \(p=\frac{ n_1 p_1 + n_2 p_2}{n_1 + n_2}\)
\(Z = \frac{{\left( {\frac{{{K_1}}}{{{n_1}}} - \frac{{{K_2}}}{{{n_2}}}} \right)}}{{\sqrt {pq(\frac{1}{{{n_1}}} + \frac{1}{{{n_2}}})} }}\) suit une loi normale centrée réduite \(\mathcal{N}(0,1)\)
4.3.3 Application et décision
La valeur \(p\), probabilité du succès commune aux deux populations n’est en réalité pas connue. On l’estime à partir des résultats observés sur les deux échantillons :
\(\hat{p} = \frac{k_1 + k_2}{n_1 + n_2}\) où \(k_1\) et \(k_2\) représentent le nombre de succès observés respectivement pour l’échantillon 1 et pour l’échantillon 2.
L’hypothèse testée est la suivante :
\(H_0 : p_1 = p_2\) contre \(H_1 : p_1 \neq p_2\)
Une valeur \(z\) de la variable aléatoire \(Z\) est calculée :
\(z = \frac{{\left| {\frac{{{k_1}}}{{{n_1}}} - \frac{{{k_2}}}{{{n_2}}}} \right|}}{{\sqrt {\hat p\hat q\left( {\frac{1}{{{n_1}}} + \frac{1}{{{n_2}}}} \right)} }}\) avec \(\hat{p} = \frac{k_1 + k_2}{n_1 + n_2}\)
z ou \(\varepsilon\) calculée (\(\varepsilon_{obs}\)) est comparée avec la valeur \(\varepsilon_{seuil}\) lue sur la table de la loi normale centrée réduite pour un risque d’erreur \(\alpha\) fixé.
si \(\varepsilon_{obs} > \varepsilon_{seuil}\) l’hypothèse \(H_0\) est rejetée au risque d’erreur \(\alpha\) : les deux échantillons sont extraits de deux populations ayant des probabilités de succès respectivement \(p_1\) et \(p_2\).
si \(\varepsilon_{obs} \leq \varepsilon_{seuil}\) l’hypothèse \(H_0\) est acceptée: les deux échantillons sont extraits de deux populations ayant même probabilité de succès \(p\).
Exemple :
On veut tester l’impact des travaux dirigés dans la réussite à l’examen de statistique.
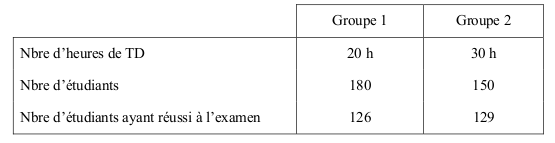
Qu’en concluez-vous ? Réponse.