Chapitre 6 — Estimation
1 Introduction
Un phénomène biologique sera entièrement déterminé si l’on connaît la loi de probabilité suivie par la variable aléatoire donnée dans la population. On a alors deux cas de figure :
soit la loi de probabilité suivie par \(X\) est connue a priori et on vérifie a posteriori que les observations faites à partir d’un échantillon sont en accord avec elle. C’est le cas par exemple de la répartition des génotypes attendus dans une population sous la loi de Mendel. On effectue alors un test de conformité entre la distribution théorique et la distribution observée (chapitre 6).
soit la loi de probabilité suivie par \(X\) est inconnue mais sugérée par la description de l’échantillon (nature de la variable, forme de la distribution des fréquences, valeurs des paramètres descriptifs) (chapitre 4). Dans ce cas, il est nécessaire d’estimer les paramètres de la loi de probabilité à partir des paramètres établis sur l’échantillon.
L’inférence statistique traite principalement de ces deux types de problèmes : l’estimation de paramètres (espérance, variance, probabilité de succés) et les tests d’hypothèses. L’inférence statistique ne conduit jamais à une conclusion stricte, elle attache toujours une probabilité à cette conclusion. Cela provient du fait que l’on tente de tirer des conclusions sur une population (grand nombre d’individus) sur la base des observations realisées sur un échantillon, représentant une portion restreinte de la population.
L’estimation a pour objectif de déterminer les valeurs inconnues des paramètres de la population (\(p\), \(\mu\), \(\sigma^2\), q) ou (proportion, moyenne, variance, paramètre quelconque) à partir des données de l’échantillon (\(f\), \(\bar{x}\), \(\sigma^2\)). Il est alors nécessaire de déterminer la précision de ces estimations en établissant un intervalle de confiance autour des valeurs prédites.
Les statistiques inférentielles ou inductives peuvent se résumer par le schéma suivant :

2 Distribution d’échantillonnage
Pour résoudre les problèmes d’estimation de paramètres inconnus, il faut tout d’abord étudier les distributions d’échantillonnage, c’est à dire la loi de probabilité suivie par l’estimateur.
Remarque : En théorie de l’estimation, il s’agit de distinguer soigneusement trois concepts différents :
les paramètres de la population comme la moyenne m dont la valeur est certaine mais inconnue symbolisés par des lettres grecques.
les résultats de l’échantillonnage comme la moyenne \(\bar{x}\) dont la valeur est certaine mais connue symbolisés par des minuscules.
les variables aléatoires des paramètres, comme la moyenne aléatoire \(\bar{X}\) dont la valeur est incertaine puisque aléatoire mais dont la loi de probabilité est souvent connue et symbolisées par des majuscules.
2.1 Définition
2.1.1 Approche empirique
Il est possible d’extraire d’une population de paramètres \(p\), \(\mu\) ou ^2$ pour une variable aléatoire \(X\), \(k\) échantillons aléatoires simples de même effectif, \(n\). Sur chaque échantillon de taille \(n\), on calcule les paramètres descriptifs (\(f\), \(\bar{x}\), \(s^2\)).
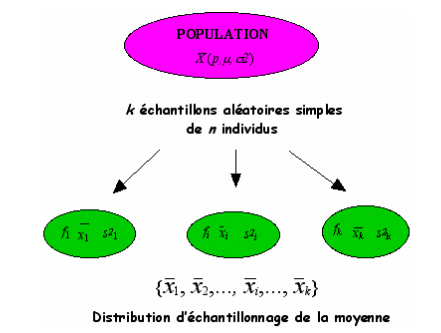
On obtient ainsi pour chaque paramètre estimé, une série statistique composée de \(k\) éléments à savoir les \(k\) estimations du paramètre étudié. Par exemple, on aura \(k\) valeurs de moyennes observées (graphe ci-dessus).
La distribution associée à ces \(k\) estimations constitue la distribution d’échantillonnage du paramètre. On peut alors associer une variable aléatoire à chacun des paramètres. La loi de probabilité suivie par cette variable aléatoire admet comme distribution, la distribution d’échantillonnage du paramètre auquel on pourra associer une espérance et une variance.
2.1.2 Approche théorique
En pratique, les données étudiées sont relatives à un seul échantillon. C’est pourquoi, il faut rechercher les propriétés des échantillons susceptibles d’être prélevés de la population ou plus précisément les lois de probabilité de variables aléatoires associées à un échantillon aléatoire.
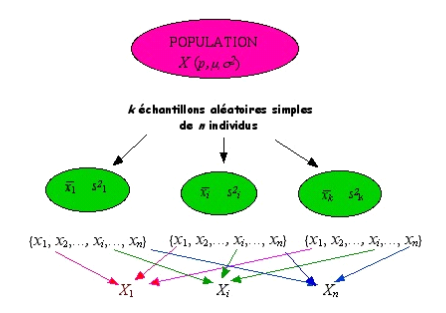
Ainsi les \(n\) observations \(x_1 , x_2 ,..., x_i , ..., x_n\), faites sur un échantillon peuvent être considérées comme \(n\) variables aléatoires \(X_1 , X_2 ,..., X_i , ..., X_n\). En effet, la valeur prise par le premier élément extrait de la population \(X_1\), dépend de l’échantillon obtenu lors du tirage aléatoire. Cette valeur sera différente si l’on considère un autre échantillon. Il en est de même pour les \(n\) valeurs extraites de la population.
A partir de ces \(n\) variables aléatoires, on peut définir alors une nouvelle variable qui sera fonction de ces dernières telle que :
\(Y = f(X_1 , X_2 ,..., X_i , ..., X_n)\)
par exemple : \(Y = X_1 + X_2 +...+ X_i + ...+ X_n\)
Ainsi la loi de probabilité de la variable aléatoire \(Y\) dépendra à la fois de la loi de probabilité de la variable aléatoire \(X\) et de la nature de la fonction \(f\).
2.2 Loi de probabilité de la moyenne
2.2.1 Définition
Soit \(X\) une variable aléatoire suivant une loi normale d’espérance \(\mu\) et de variance \(\sigma^2\) et \(n\) copies indépendantes \(X_1 , X_2 ,..., X_i , ..., X_n\) telle que \(X_i\) associe le ième élément de chacun des \(n\) échantillons avec \(E(X_i) = \mu\) et \(V(X)=\sigma^2\)
On construit alors la variable aléatoire \(\bar{X}\), telle que
\(\bar{X}= \frac{{X_1} + {X_2} + ... + {X_i} + ... + {X_n}}{n} = \frac{1}{n}\sum\limits_{i = 1}^n {{X_i}}\)
avec pour espérance :
\(E(\bar{X)}= E(\frac{1}{n}\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{n}E(\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{n}\sum\limits_{i = 1}^n {E({X_i}} ) = \frac{1}{n}n\mu\)
d’où \(E(\bar{X)}= \mu\) \(\qquad E(\bar{X)}\) est notée également \({\mu_{\bar{X}}}\)
et pour variance si \(V(X_i) = \sigma^2\) :
\(V(\bar{X)}= V(\frac{1}{n}\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{{{n^2}}}V(\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{{{n^2}}}\sum\limits_{i = 1}^n {V({X_i}} ) = \frac{1}{{{n^2}}}n{\sigma ^2}\)
d’où \(V(\bar{X)}= \frac{{{\sigma ^2}}}{n}\) \(\qquad V(\bar{X)}\) est notée également \(\sigma_{\bar{X}^2}\)
La loi de probabilité de la variable aléatoire \(\bar{X}\), moyenne de \(n\) v.a. \(X\) de loi de probabilité \(\mathcal{N}(\mu , \sigma )\), est une loi normale \(\mathcal{N}(\mu , \frac{\sigma}{\sqrt{n}})\).
Remarque : il est aisé de voir sur le graphe ci-dessous que la variance associée à une moyenne (\(\frac{\sigma ^2}{n}\)) est plus faible que la variance de la variable elle-même (\(\sigma^2\)).

Soit l’étendue des valeurs observées d’une variable aléatoire \(X\) pour 4 échantillons de même taille d’une même population.
Les valeurs des moyennes arithmétiques sont indiquées ainsi que les limites relatives à l’étendue des valeurs de la variable observée et celle des moyennes observées.
Exemple :
Des études statistiques montrent que le taux de glucose dans le sang est une variable normale \(X\) d’espérance \(\mu = 1\) g/l et d’écart-type \(\sigma = 0,1\) g/l.
En prenant un échantillon de 9 individus dans la population, l’espérance et l’écart-type théorique attendu de la variable aléatoire \(\bar{X}\) sont alors :
\({\mu_{\bar{X}}} = \mu = 1\) g/l et \(\sigma_{\bar{X}} = \frac{\sigma }{\sqrt n} = \frac{0,1}{\sqrt 9} =\) 0,03 g/l
2.2.2 Convergence
En fonction de la nature de la variable aléatoire continue \(X\), de la taille de l’échantillon \(n\) et de la connaissance que nous avons sur le paramètre \(\sigma^2\), la variable centrée réduite construite avec \(\bar{X}\) converge vers différentes lois de probabilité (Table de convergence).
Lorsque \(\sigma^2\) est connue et \(n\) grand (\(n \geq 30\)), on se trouve dans les conditions du théorème central limite et la loi suivie par :
\(\frac{\bar{X} - \mu}{\sigma / {\sqrt n}} = \mathcal{N}(0,1) \quad\) loi normale réduite
Ceci reste vrai lorsque \(n \leq 30\) seulement si la loi suivie par \(X\) suit une loi normale.
Lorsque la variance \(\sigma^2\) est inconnue et \(X\) suit une loi normale, la loi suivie par la variable centrée réduite est alors: \(\frac{\bar{X}- \mu }{\hat{\sigma} / {\sqrt n }} \to T_{n-1}\) loi de student à \(n-1\) degrés de liberté
Lorsque \(n \geq 30\), la loi de student tend vers une loi normale réduite (voir convergence).
Lorsque \(\sigma^2\) est inconnue et \(X\) ne suit pas une loi normale, la loi suivie par
\(\frac{\bar{X}- \mu }{\hat{\sigma} / {\sqrt n }}\) n’est pas connue.
2.3 Loi de probabilité d’une fréquence
Soit une population dans laquelle une proportion \(p\) des individus présente une certaine propriété.
Si \(k\) est le nombre d’individu présentant la propriété dans un échantillon de taille \(n\), alors la variable aléatoire \(K\) résultant de différents échantillonnages suit une loi binomiale \(\mathcal{B}(n,p)\) avec \(E(K) = np\) et \(V(K) = npq\).
On construit la variable aléatoire \(F = \frac{K}{n}\) avec
pour espérance : \(E(F) = E(\frac{K}{n}) = \frac{1}{n}E(K) = \frac{1}{n}np = p\)
et pour variance : \(V(F) = V(\frac{K}{n}) = \frac{1}{n^2}V(K) = \frac{1}{n^2}npq = \frac{pq}{n}\)
La loi de probabilité d’une fréquence \(\frac{K}{n}\), suit une loi normale $ (p, \(\sqrt{\frac{pq}{n}})\)
vrai si \(np > 5\) et \(nq > 5\).
3 Estimateur
3.1 Définition
Soient \({X_1},{X_2},...,{X_i},...,{X_n}\) réalisations indépendantes de la variable aléatoire \(X\) (discrète ou continue) et \(\theta\) un paramètre associé à la loi de probabilité suivi par \(X\), un estimateur du paramètre \(\theta\) est une variable aléatoire \(\Theta\) fonction des \(X_i\) :
\(\Theta = f({X_1},{X_2},...,{X_i},...,{X_n})\)
Si on considère \(n\) observations \({x_1},{x_2},...,{x_i},...,{x_n}\), l’estimateur \(\Theta\) fournira une estimation de \(\theta\) notée également \(\hat \theta\):
\(\hat \theta = f({x_1} + {x_2} + ... + {x_i} + ... + {x_n})\)
L’estimation d’un paramètre inconnu, noté \(\theta\) est fonction des observations résultant d’un échantillonnage aléatoire simple de la population. L’estimateur est donc une nouvelle variable aléatoire construite à partir des données expérimentales et dont la valeur se rapproche du paramètre que l’on cherche à connaître.
L’estimation de \(\theta\) est une variable aléatoire \(\Theta\) dont la distribution de probabilité s’appelle la distribution d’échantillonnage du paramètre \(\theta\). L’estimateur \(\Theta\) admet donc une espérance \(E(\Theta)\) et une variance \(V(\Theta)\).
3.2 Propriétés
3.2.1 Convergence
L’estimateur \(\Theta\) doit tendre vers la valeur réelle du paramètre \(\theta\) lorsque le nombre d’individus étudié augmente. On dit que l’estimateur est convergent.
si \(\forall \varepsilon > 0 \quad P(| \Theta - \theta | ) > \varepsilon \to 0\) lorsque \(n \to \infty\)
Ceci équivaut à dire qu’en limite \(\Theta \to \theta\) lorsque \(n \to \infty\).
3.2.2 Biais d’un estimateur
Le biais d’un estimateur noté \(B(\Theta)\) est la différence moyenne entre sa valeur et celle du paramètre qu’il estime. Le biais doit être égal à 0 pour avoir un bon estimateur.
\(B(\Theta) = E(\Theta - \theta) = E(\Theta) - E(\theta) = E(\Theta) - \theta = 0\) (voir propriétés de l’espérance)
d’où \(E(\Theta) = \theta\)
Ainsi l’estimateur sera sans biais si son espérance est égale à la valeur du paramètre de la population.
\(E(\Theta) = \theta\)
Exemple :
Soit les densités de probabilité de 3 estimateurs d’une espérance \(\mu\),

Dans l’exemple ci-dessus, \(\Theta_1\) et \(\Theta_2\) sont des estimateurs sans biais de \(\mu\) car \(B(\Theta_1) = E(\Theta_1- \mu) = E(\Theta_1) - \mu = 0\) car \(E(\Theta_1) - \mu\), de même pour \(B(\Theta_2)\)
alors que \(\Theta_3\) est un estimateur biaisé de \(\mu\) car
\(B(\Theta_3) = E(\Theta_3 - \mu) = E(\Theta_3) - \mu = \mu' - \mu \neq 0\) car \(E(\Theta_3) = \mu'\)
Remarque: Un estimateur est asymptotiquement sans biais si \(E(\Theta) \to \theta\) lorsque \(n \to \infty\).
3.2.3 Variance d’un estimateur
Si deux estimateurs sont convergents et sans biais, le plus efficace est celui qui a la variance la plus faible car ses valeurs sont en moyenne plus proches de la quantité estimée.
\(V(\Theta) = E(\Theta - E(\Theta))^2\) minimale
Exemple :
Dans l’exemple précédent, on voit que \(V(\Theta_1) < V(\Theta_2)\). On peut donc conclure que \(\Theta_1\) est un meilleur estimateur de \(\mu\) que \(\Theta_2\).
Remarque : Quand les estimateurs sont biaisés, en revanche, leur comparaison n’est pas simple. Ainsi un estimateur peu biaisé mais de variance très faible, pourrait même être préféré à un estimateur sans biais mais de grande variance.
Théorème :
Si un estimateur est asymptotiquement sans biais et si sa variance tend vers 0 lorsque \(n \to \infty\), il est convergent.
\(P( | \Theta - \theta | \geq \varepsilon) \leq \frac{V(\Theta)}{\varepsilon^2}\) avec \(\varepsilon > 0\)
Cette inégalité exprime que si \(|\Theta - \theta|\) tend vers 0 quand \(n\) augmente, \(V(\Theta)\) doit aussi tendre vers 0.
4 Estimation ponctuelle et par intervalle
L’estimation d’un paramètre quelconque \(\theta\) est ponctuelle si l’on associe une seule valeur à l’estimateur \(\hat \theta\) à partir des données observables sur un échantillon aléatoire. L’estimation par intervalle associe à un échantillon aléatoire, un intervalle [\({\hat \theta_1},{\hat \theta_2}\)] qui recouvre \(\theta\) avec une certaine probabilité.
4.1. Estimation ponctuelle
Si la distribution de la variable aléatoire \(X\) est connue, on utilise la méthode du maximum de vraisemblance pour estimer les paramètres de la loi de probabilité. En revanche si la distribution n’est pas connue, on utilise la méthode des moindres carrés.
4.1.1. Espérance
Soit \(X\) une variable aléatoire continue suivant une loi normale \(\mathcal{N}(\mu,\sigma)\) dont la valeur des paramètres n’est pas connue et pour laquelle on souhaite estimer l’espérance \(\mu\).
Soient \({X_1},{X_2},...,{X_i},...,{X_n}\), \(n\) réalisations indépendantes de la variable aléatoire \(X\), un estimateur du paramètre \(\mu\) est une suite de variable aléatoire \(\Theta\) fonctions des \(X_i\) :
\(\Theta = f(X_1,X_2,...,X_i,...,X_n)\)
La méthode des moindres carrés consiste à rechercher les coefficients de la combinaison linéaire
\(\Theta = {a_1}{X_1} + {a_2}{X_2} + ... + {a_i}{X_i} + ... + {a_n}{X_n}\)
telle que \(E(\Theta)= \mu\) et \(V(\Theta)\) soit minimale (voir démonstration)
La moyenne arithmétique constitue le meilleur estimateur de \(\mu\), espérance de la loi de probabilité de la variable aléatoire \(X\) :
\(\hat \mu = \bar{X} = \frac{1}{n}\sum\limits_{i = 1}^n {{X_i}}\)
Voici pourquoi :
Estimateur sans biais : \(E(\bar{X}) = \mu\) (voir loi de la moyenne)
Estimateur convergent : si l’on pose l’inégalité de Biénaymé-Tchébycheff :
\(P( | \bar{X} - \mu | \geq \varepsilon) \leq \frac{V(\bar X)}{\varepsilon^2}\) avec \(\varepsilon > 0\)
lorsque \(n \to \infty \qquad \frac{V(\bar{X})}{\varepsilon^2}= \frac{\sigma^2}{n \varepsilon^2}\) et ceci ainsi en limite, \(P( | \bar{X} - \mu | \geq \varepsilon ) = 0\) ce qui indique que \(\bar{X} \to \mu\) en probabilité.
4.1.2. Variance
Soit \(X\) une variable aléatoire continue suivant une loi normale \(\mathcal{N}(\mu,\sigma)\) pour laquelle on souhaite estimer la variance \(\sigma^2\).
Soient \(X_1,X_2,...,X_i,...,X_n\) réalisations indépendantes de la variable aléatoire \(X\), un estimateur du paramètre \(\sigma^2\) est une suite de variable aléatoire \(\Theta\) fonctions des \(X_i\):
\(\Theta = f({X_1} + {X_2} + ... + {X_i} + ... + {X_n})\)
- Cas où l’espérance \(\mu\) est connue
La méthode des moindres carrés consiste à rechercher les coefficients de la combinaison linéaire
\(\Theta = a_1(X_1 - \mu )^2 + a_2(X_2 - \mu )^2 + ... + a_i(X_i - \mu )^2 + ... + a_n(X_n - \mu )^2\)
telle que \(E(\Theta) = \sigma^2\) et \(V(\Theta)\) soit minimale (voir démonstration)
La variance observée constitue le meilleur estimateur de \(\sigma^2\), variance de la loi de probabilité de la variable aléatoire \(X\) lorsque \(\mu\) est connue:
\({\hat \sigma ^2} = \frac{1}{n}\sum\limits_{i * 1}^n {({X_i}} - \mu {)^2}\)
Remarque : Cette estimation de la variance de la population est rarement utilisée dans la mesure où si la variance \(\sigma^2\) n’est pas connue, l’espérance \(\mu\) ne l’est pas non plus.
- Cas où l’espérance \(\mu\) est inconnue
Dans ce cas, nous allons estimer m avec \(\hat \mu = \bar{X}\) et dans ce cas \(\sum\limits_{i = 1}^n {{({X_i} - \mu )}^2} \ne \sum\limits_{i = 1}^n {({X_i}} - \bar{X{)^2}}\). Nous allons étudier la relation entre ces deux termes à partir de la variance observée :
\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \bar{X{)^2}}= \frac{1}{n}\sum\limits_{i = 1}^n {[({X_i}} - \mu ) - (\bar{X}- \mu ){]^2}\)
\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {[({X_i}} - \mu {)^2} + {(\bar{X}- \mu )^2} - 2({X_i} - \mu )(\bar{X}- \mu ){]^{}}\)
\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \mu {)^2} + \frac{1}{n}\sum\limits_{i = 1}^n {{{(\bar{X}- \mu )}^2}} - 2(\bar{X}- \mu ){\sum\limits_{i = 1}^n {({X_i} - \mu )} ^{}}\) avec \({\sum\limits_{i = 1}^n {({X_i} - \mu )} ^{}}\)= \(n(\bar{X}- \mu )\)
\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \mu {)^2} + {(\bar{X}- \mu )^2} - 2{(\bar{X}- \mu )^2}\)
\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \mu {)^2} - {(\bar{X}- \mu )^2} = {\sigma ^2} - \frac{{{\sigma ^2}}}{n}\) en effet \(\sigma_{\bar{X}^2}= \frac{1}{n}\sum\limits_{i = 1}^n {(\bar{X}}- \mu {)^2} = {(\bar{X}- \mu )^2} = \frac{{{\sigma ^2}}}{n}\)
ainsi \({s^2} = \frac{{n - 1}}{n}{\sigma ^2}\)
Le meilleur estimateur de \(\sigma^2\), variance de la loi de probabilité de la variable aléatoire \(X\) lorsque \(\mu\) est inconnue est : \({\hat \sigma ^2} = \frac{n}{{n - 1}}{s^2} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {({X_i}} - \bar{X{)^2}}\)
Remarque : Lorsque \(n\) augmente, la variance observée \(s^2\) tend vers la variance de la population \(\sigma^2\).
\(\lim\limits_{n \to + \infty } s^2 = \lim\limits_{n \to + \infty } \frac{n-1}{n} \sigma^2 = \sigma^2\)
4.1.3. Fréquence
Soit le schéma de Bernoulli dans lequel le caractère A correspond au succés. On note \(p\) la fréquence des individus de la population possédant le caractère A. La valeur de ce paramètre étant inconnu, on cherche à estimer la fréquence \(p\) à partir des données observables sur un échantillon.
A chaque échantillon non exhaustif de taille \(n\), on associe l’entier \(k\), nombre d’individus possédant le caractère A.
Soit \(K\) une variable aléatoire discrète suivant une loi binomiale \(\mathcal{B}(n,p)\) et pour laquelle on souhaite estimer la fréquence \(p\).
La fréquence observée du nombre de succès observé dans un échantillon de taille \(n\) constitue le meilleur estimateur de \(p\):
\(\hat p = \frac{K}{n}\)
Voici pourquoi :
Estimateur sans biais : \(E(\frac{K}{n}) = p\) (voir loi d’une fréquence)
Estimateur convergent : si l’on pose l’inégalité de Biénaymé-Tchébycheff :
\(P( | \frac{K}{n} - p | \geq \varepsilon ) \leq \frac{V(\frac{K}{n})}{\varepsilon ^2}\) avec \(\varepsilon > 0\)
alors lorsque \(n \to \infty \quad \frac{V(\frac{K}{n})}{\varepsilon ^2} = \frac{pq}{n{\varepsilon ^2}} \to 0\) et ceci \(\forall \varepsilon > 0\)
ainsi en limite \(P(| \frac{K}{n}- p| \geq \varepsilon ) = 0\) ce qui indique que \(\frac{K}{n} \to p\) en probabilité.
Remarque : Nous avions déjà avancé cette propriété lors de l’établissement de la loi des grands nombres.
Exemple :
On a prélevé au hasard, dans une population de lapin, 100 individus. Sur ces 100 lapins, 20 sont atteints par la myxomatose. Le pourcentage de lapins atteints par la myxomatose dans la population est donc : \(\hat{p} = \frac{K}{n} = \frac{20}{100}\) = 0,2 soit 20% de lapins atteins dans la population
Ce résultat n’aura de signification que s’il est associé à un interval de confiance.
4.2. Estimation par intervalle
4.2.1. Définition
L’estimation par intervalle associe à un échantillon aléatoire, un intervalle [\(\hat{\theta_1}\),\(\hat{\theta_2}\)] qui recouvre \(\theta\) avec une certaine probabilité.
Cet intervalle est appelé l’intervalle de confiance du paramètre \(\theta\) car la probabilité que \(\theta\) dont la valeur est inconnue se trouve compris entre \(\hat{\theta_1}\) et \(\hat{\theta_2}\) est égale à \(1 - \alpha\) , le coefficient de confiance.
\(P(\hat{\theta_1} < \theta < \hat {\theta_2}) = 1 - \alpha\)
Son complément \(\alpha\) correspond au coefficient de risque.
\(P( \theta \ne [ \hat{\theta_1} , \hat{\theta_2} ] ) = \alpha\)
Un intervalle de confiance indique la précision d’une estimation car pour un risque \(\alpha\) donné, l’intervalle est d’autant plus grand que la précision est faible comme l’indiquent les graphes ci-dessous. Pour chaque graphe, l’aire hachurée en vert correspond au coefficient de risque \(\alpha\). Ainsi de part et d’autre de la distribution, la valeur de l’aire hachurée vaut \(\frac{\alpha }{2}\).

4.2.2 Intervalle de confiance d’une moyenne
En fonction de la nature de la variable aléatoire continue \(X\), de la taille de l’échantillon \(n\) et de la connaissance que nous avons sur le paramètre \(\sigma^2\), l’établissement de l’intervalle de confiance autour de \(\mu\) sera différent.
- Quelque soit la valeur de \(n\), si \(X \to \mathcal{N} (\mu , \sigma )\) et \(\sigma^2\) est connue, établir l’intervalle de confiance autour de la moyenne \(\mu\) revient à établir la valeur de \(i\) pour une valeur du coefficient de confiance 1 - a donnée par l’expérimentateur.
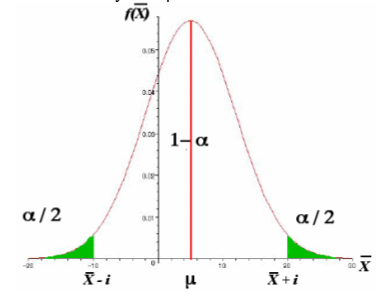
Voici comment :
Si \(P(\bar{X} - i < \mu < \bar{X}+ i ) = 1 - \alpha\) alors \(P(\mu - i < bar{X} < \mu + i ) = 1 - \alpha\)
Connaissant la loi suivie par la v.a. \(\bar{X}\) et d’après le théorème central limite, on peut établir que \(P(\frac{ - i}{\sigma / \sqrt {n} } < \frac{\bar{X}- \mu }{\sigma / \sqrt{n} } < \frac{ + i}{\sigma / \sqrt {n} }) = 1 - \alpha\) sachant que \(\frac{\bar{X}- \mu }{ \sigma /\sqrt {n} } \to \mathcal{N}(0,1)\) (conditions)
par conséquence \(\left| \frac{i}{\sigma / \sqrt{n} } \right|\) correspond à la valeur de la variable normale réduite pour probabilité \(\alpha\) donnée notée \(\varepsilon_{\alpha}\) ou écart réduit.
ainsi \(\left| \frac{i}{\sigma /\sqrt {n}} \right| = \varepsilon_{\alpha}\) implique \(i = \varepsilon_{\alpha} \times \frac{\sigma }{\sqrt {n} }\)
L’intervalle de confiance de la moyenne \(\mu\) pour un coefficient de risque \(\alpha\) est donc
\(\bar{X} - \varepsilon_{\alpha} \frac{\sigma }{\sqrt {n} } < \mu < \bar{X}+ \varepsilon_{\alpha} \frac{\sigma }{\sqrt {n}}\)
quelque soit la valeur de \(n\) si \(X \to \mathcal{N}(\mu,\sigma)\) et \(\sigma^2\) est connue
Exemple :
Pour des masses comprises entre 50g et 200g, une balance donne une pesée avec une variance de 0,0015. Les résultats des trois pesées d’un même corps sont : 64,32 ; 64,27 ; 64 ,39.
On veut connaître le poids moyen de ce corps dans la population avec un coefficient de confiance de 99%.
avec \(\bar{X}\)= 64,33 et \(\varepsilon_{\alpha}\)= 2,576 alors \(\varepsilon_{\alpha} \frac{\sigma}{\sqrt {n} } = 2,576 \times \frac{0,039}{1,732}\)= 0,058
et donc \(\mu = \bar{X} \pm \varepsilon_{\alpha} \frac{\sigma }{\sqrt n}\) = 64,33g ± 0,058
d’où le poids moyen de ce corps est compris dans l’intervalle [64,27 ; 64,39] avec une probabilité de 0,99.
Remarque : La valeur de \(\varepsilon_{\alpha}\) est donnée par la table de l’écart-réduit pour une valeur \(\alpha\) donnée.

- Quelque soit la valeur de \(n\), si \(X \to (\mu , \sigma )\) et \(\sigma^2\) est inconnue
Le raisonnement reste le même mais la variance de la population \(\sigma^2\) doit être estimée par
\(\hat{\sigma ^2} = \frac{n}{n - 1} s^2\) (voir estimation ponctuelle)
Si \(P( \bar{X} - i < \mu < \bar{X} + i ) = 1 - \alpha\) alors \(P(\mu - i < bar{X} < \mu + i ) = 1 - \alpha\)
Connaissant la loi suivie par la v.a. \(\bar{X}\) et celle suivie par la variable centrée réduite, on peut établir que \(P\left( \frac{ - i}{ \hat {\sigma} / \sqrt{n} } < \frac{ \bar{X} - \mu }{ \hat{\sigma} / \sqrt {n} } < \frac{ +i}{\hat{\sigma} / \sqrt {n} } \right) = 1 - \alpha\) sachant que \(\frac{\bar{X}- \mu}{\hat{\sigma} / \sqrt{n} } \to T(n-1 \ \text{d.d.l.})\) (conditions)
par conséquence \(\left| \frac{i}{\hat{\sigma} / \sqrt {n} } \right|\) correspond à la valeur de la variable de student pour une valeur de probabilité a donnée notée \(t_{\alpha}\) pour \(n - 1\) degrés de liberté.
Ainsi \(\left| \frac{i}{ \hat{\sigma} / \sqrt{n} } \right| = t_{\alpha}\) implique \(i = t_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}}\)
L’intervalle de confiance de l’espérance \(\mu\) pour un coefficient de risque \(\alpha\) est donc \(\bar{X} - t_{\alpha} \frac{\hat{\sigma}}{\sqrt {n}} < \mu < \bar{X} + t_{\alpha}\frac{\hat {\sigma}}{\sqrt {n}}\) quelque soit la valeur de \(n\) si \(X \to \mathcal{N}(\mu , \sigma )\) et \(\sigma^2\) est inconnue
Remarque : Lorsque \(n > 30\) la loi de student converge vers une loi normale réduite ainsi la valeur de \(t_{\alpha}(n-1)\) est égale à \(\varepsilon_{\alpha}\). Ci-dessous, un exemple pour un risque \(\alpha = 0,05\)

Exemples :
- Dans un échantillon de 20 étudiants de même classe d’âge et de même sexe, la taille moyenne observée est de 1,73m et l’écart-type de 10 cm. La taille moyenne de l’ensemble des étudiants de l’université est donc :
avec \(\bar{x} =\) 1,73m ; \(\hat{\sigma^2} = \frac{n}{n - 1} s^2 = \frac{20}{19} \times 0,01=\) 0,011 et \(t_{\alpha} =\) 2,086
d’où \(t_{\alpha} \frac{\hat {\sigma}}{\sqrt {n} } = 2,086 \times \sqrt {\frac{0,011}{20}} =\) 0,049 ainsi \(\mu = \bar{X} \pm t_{\alpha} \frac{\hat{\sigma} }{ \sqrt {n}} =\) 1,73 ± 0,049
La taille moyenne des étudiants dans la population est comprise dans l’intervalle [1,68 ; 1,78] avec une probabilité de 0,95.
- Dans un échantillon de 100 étudiants, la taille moyenne de la population est :
\(\bar{x} =\) 1,73m ; \({\hat \sigma ^2} = \frac{n}{n - 1} s^2 = \frac{100}{99} \times 0,01=\) 0,01 et \(\varepsilon_{\alpha}=\) 1,960
d’où \(\varepsilon_{\alpha} \frac{{\hat \sigma }}{{\sqrt n }} = 1,960 \times \sqrt {\frac{{0,010}}{{100}}} =\) 0,02 ainsi \(\mu = \bar{X}\pm {\varepsilon_\alpha }\frac{{\hat \sigma }}{{\sqrt n }}\) = 1,73 ± 0,02
La taille moyenne des étudiants dans la population est comprise dans l’intervalle [1,71 ; 1,75] avec une probabilité de 0,95.
Ainsi lorsque la taille de l’échantillon augmente pour un même coefficient de confiance \((1- \alpha)\) , l’estimation autour de m est plus précise.
- Si \(n > 30\) et \(X\) suit une loi inconnue
La démarche est la même que pour le cas précédent puisque par définition la variance de la population est inconnue et doit être estimée avec la variance observée :
\({\hat \sigma ^2} = \frac{n}{{n - 1}}{s^2}\) (voir estimation ponctuelle)
Comme pour le cas 1, la loi suivie par la variable centrée réduite \(\frac{{\bar{X}- \mu }}{{\hat \sigma /\sqrt n }} \to \mathcal{N}(0,1)\) (conditions).
L’intervalle de confiance de l’espérance \(\mu\) pour un coefficient de risque \(\alpha\) est donc \(\bar{X}- \varepsilon_{\alpha} \frac{\hat {\sigma}}{\sqrt {n} } < \mu < \bar{X} + \varepsilon_{\alpha} \frac{\hat {\sigma}}{{\sqrt n}}\)
vraie seulement si \(n\) est grand
- Si \(n < 30\) et \(X\) suit une loi inconnue,
La loi de probabilité suivie par \(\frac{\bar{X}- \mu}{\hat{\sigma} / \sqrt {n} }\) n’est pas connue et l’on a recours aux statistiques non paramétriques.
4.2.3 Intervalle de confiance d’une proportion
Etablir l’intervalle de confiance autour de la fréquence \(p\) de la population à partir de son estimateur \(\frac{K}{n}\) revient à établir la valeur de \(i\) pour une valeur du coefficient de confiance \((1 - \alpha)\) donnée par l’expérimentateur telle que :
\(P(\frac{K}{n} - i < p < \frac{K}{n} + i ) = 1 - \alpha\) ou \(P(p - i < \frac{K}{n} < p + i ) = 1 - \alpha\)
Connaissant la loi suivie par la v.a. \(\frac{K}{n}\) et d’après le théorème central limite, on peut établir que \(P(\frac{ - i}{\sqrt {\frac{pq}{n}}} < \frac{\frac{K}{n} - p}{\sqrt {\frac{pq}{n}}} < \frac{ + i}{\sqrt {\frac{pq}{n}} }) = 1 - \alpha\) sachant que \(\frac{\frac{K}{n} - p}{\sqrt {\frac{pq}{n}} } \to \mathcal{N}(0,1)\)
par conséquence \(\left| {\frac{i}{\sqrt {\frac{pq}{n}} }} \right|\) correspond à la valeur de la variable normale réduite pour probabilité a donnée notée \(\varepsilon_{\alpha}\) ou écart réduit.
ainsi \(\left| {\frac{i}{\sqrt{\frac{pq}{n}}}} \right| = \varepsilon_{\alpha}\) implique \(i = \varepsilon_{\alpha} \times \sqrt{\frac{pq}{n}}\)
Par définition, \(V(\frac{K}{n})= \frac{pq}{n}\) n’est pas connue et on l’estime par \(\frac{\hat p \hat q}{n}\) avec \(\hat p = \frac{K}{n}\) et \(\hat q = \frac{n - K}{n}\)
L’intervalle de confiance de la fréquence \(p\) pour un coefficient de risque \(\alpha\) est donc
\(\frac{K}{n} - {\varepsilon_\alpha }\sqrt {\frac{{\hat p\hat q}}{n}} < p < \frac{K}{n} + {\varepsilon_\alpha }\sqrt {\frac{{\hat p\hat q}}{n}}\)
vraie seulement si \(n\) est grand et \(np, nq > 5\)
Remarque : Si la taille de l’échantillon est faible, on a recours aux lois exactes.
Exemple :
Un laboratoire d’agronomie a effectué une étude sur le maintien du pouvoir germinatif des graines de Papivorus subquaticus après une conservaion de 3 ans.
Sur un lot de 80 graines, 47 ont germé. Ainsi la probabilité de germination des graines de Papivorus subquaticus après trois ans de conservation avec un coefficient de confiance de 95% est donc :
avec \(\hat p = \frac{K}{n} = \frac{47}{80} = 0,588\) , \(\hat q = \frac{n - K}{n} = \frac{33}{80} = 0,412\) et \(\varepsilon_\alpha= 1,96\)
alors \({\varepsilon_\alpha }\sqrt {\frac{{\hat p\hat q}}{n}} = 1,96 \times \sqrt {\frac{0,588 \times 0,412}{80}} = 0,108\) d’où \(p =\) 0,588 ± 0,108
ainsi la probabilité de germination est comprise dans l’intervalle [0,480 et 0,696] avec une probabilité de 0,95.