Chapitre 2 — Probabilités
1. Introduction
Les premières personnes à s’être intéressées aux problèmes des probabilités furent des mathématiciens français, Blaise Pascal et Pierre de Fermat qui répondaient aux questions soulevées par un adepte des jeux de hasard, le chevalier de Méré. A cette époque, la théorie des probabilités se développa uniquement en relation avec les jeux de hasard. Mais avec Pierre Simon Laplace et Karl Friedrich Gauss , les bases de la théorie furent étendues à d’autres applications et phénomènes.
Le calcul des probabilités fournit une modélisation efficace des situations non déterministes c’est-à-dire des phénomènes aléatoires ou stochastiques. En ce qui concerne les premiers, le résultat d’une expérience suit une loi rigoureuse connue (taux de croissance d’une population bactérienne). On peut donc ainsi prévoir le résultat pour un événement donné. En revanche dans le cas des phénomènes aléatoires, le résultat de l’expérience n’est pas connu avec certitude mais fluctue autour d’un résultat moyen qui est régit par une loi (transmission des caractères selon la loi de Mendel).
Il existe deux manières d’introduire la notion de probabilité :
La probabilité a priori, « subjective » d’un événement est un nombre qui caractérise la croyance que l’on a que cet événement est réalisé avec plus ou moins de certitude avant l’exécution de l’expérience : l’événement est réalisé (probabilité 1) et l’événement n’est pas réalisé (probabilité 0).
La probabilité empirique, assimilée à une fréquence est définie à partir d’expériences indéfiniment renouvelables. La probabilité d’un événement est alors la fréquence d’apparition de cet événement.
Enfin le calcul des probabilités utilise l’analyse combinatoire ainsi que la théorie des ensembles.
2. Espace fondamental et évènements
La théorie des ensembles qui est succinctement présentée dans ce chapitre constitue un outil puissant dans plusieurs branches des mathématiques, notamment en probabilités.
2.1 Définitions
En face de situations dont l’issue est incertaine, on a bien souvent envie d’attribuer à chacune des éventualités possibles une vraisemblance plus ou moins grande. Afin de donner une rigueur mathématique à ce concept, il est nécessaire tout d’abord de donner quelques définitions.
Une expérience ou une épreuve est qualifiée d’aléatoire si on ne peut pas prévoir son résultat et si, répétée dans des conditions identiques, elle peut donner des résultats différents.
Le résultat d’une expérience noté \(\omega\) constitue une éventualité ou un événement élémentaire.
L’ensemble des évènements élémentaires possibles pour une expérience aléatoire donnée constitue l’espace fondamental appelé univers ou univers des possibles noté \(\Omega\).
Exemple:
Lors d’un contrôle sanguin, l’ensemble des résultats possibles si l’on s’intéresse
au groupe sanguin et au facteur rhésus d’un individu est \(\Omega = \{ \text{A+, A-, B+, B-, AB+, AB-, O+, O-} \}\)
au nombre de globules blancs \(\Omega = {\mathbb{N}^*} = \{1,2,....,n,... \}\)
au taux de glycémie \(\Omega = [0; 15]\) au-delà de 15, l’individu n’est plus en état de subir une prise de sang.
Ainsi pour une même épreuve, l’univers \(\Omega\) peut être fini (toutes les éventualités sont connues : cas 1) ou infini (toutes les éventualités ne sont pas connues : cas 2 et 3). Dans ces deux derniers cas, l’univers peut être dénombrable si on peut numéroter les éventualités connues (cas 2) ou bien continu comme dans le cas du taux de glycémie (cas 3).
Un événement quelconque \(A\) est un ensemble d’évènements élémentaires et constitue une partie de l’univers des possibles \(\Omega\) dont on sait dire à l’issue de l’épreuve s’il est réalisé ou non.
Si \(\omega \in A\), alors \(A\) est réalisé. Mais si \(\omega \notin A\) alors \(A\) n’est pas réalisé et c’est \(\bar{A}\) , l’événement contraire qui est réalisé. Un événement est donc une assertion relative aux résultats d’une expérience.
Il est possible qu’un événement ne soit constitué que d’un seul événement élémentaire.
Les évènements sont représentés par des lettres majuscules \(A,B,C,A_1,A_2\), etc.
Exemple:
Dans l’exemple concernant les groupes sanguins,
l’événement \(A\) « l’individu est de rhésus positif » est représenté par : \(A = \{\text{A+,B+,AB+,O+}\} \qquad \text{avec} \qquad A \subset \Omega\)
l’événement \(B\) « l’individu est donneur universel » est représenté par : \(B = \{\text{O-}\}\) un seul événement élémentaire
Dans le cadre de cet exemple, l’événement \(A\) est réalisé si le résultat du typage donne l’un des 4 groupes sanguins \(\text{A+,B+,AB+,O+}\).
Remarque : Pour ce même exemple, le résultat « la glycémie vaut \(\sqrt{2}\) » ne constitue pas un événement car il est impossible de savoir s’il est réalisé ou non. Toute partie de \(\Omega\) n’est pas forcément un événement. Ainsi il faut toujours définir après avoir déterminé l’univers \(\Omega\), l’ensemble des évènements \(\varepsilon(\Omega)\).
Si \(\Omega\) est fini, chaque partie \(A\) de l’univers \(\Omega (A \subset \Omega)\) est constituée d’un nombre fini d’éventualités et dans ce cas l’ensemble des évènements est tel que :
\(\varepsilon(\Omega) = \mathcal{P}(\Omega)\) l’univers des possibles
Dans le cadre de ce cours, nous nous placerons dans le cas où l’ensemble des évènements de l’univers \(\Omega\) est clairement défini.
2.2. Evènements remarquables
L’événement impossible, noté \(\emptyset\) est l’événement qui ne peut être réalisé quelle que soit l’issue de l’épreuve. Bien que constitué d’aucune éventualité, \(\emptyset\) est considéré comme un événement :
\(\emptyset \in \varepsilon(\Omega)\)
L’événement certain, noté \(\Omega\) est toujours réalisé quelle que soit l’issue de l’épreuve. Il est constitué de toutes les éventualités et l’on impose que ce soit un événement :
\(\Omega \in \varepsilon(\Omega)\)
L’événement contraire ou complémentaire d’un événement \(A\), noté \(\mathcal{C}_{A}\) ou \(\bar{A}\) est l’événement qui est réalisé si et seulement si \(A\) ne l’est pas. Il est donc constitué des évènements élémentaires \(\omega\) qui ne sont pas dans \(A\).
\(\omega \in \bar{A} \Leftrightarrow \omega \notin A\)
Le complémentaire \(\mathcal{C}_{A}\) ou \(\bar{A}\) correspond à la négation logique non–A.
Exemple:
Dans l’exemple concernant les groupes sanguins, l’événement contraire de \(A\) « l’individu est de rhésus positif » est constitué des évènements élémentaires suivant : \(\bar{A} = \{\text{A-, B-, AB-, O-}\}\)
Par définition, on obtient les relations suivantes :
\(\bar{\bar{A}} = A\)
\(\bar{\emptyset} = \Omega\)
\(\bar{\Omega} = \emptyset\)
2.3. Opérations sur les évènements
Si l’on considère simultanément la réalisation de deux évènements \(A\) et \(B\), il est possible d’effectuer des opérations sur ces ensembles.
2.3.1. L’intersection de deux évènements
On appelle intersection de deux évènements \(A\) et \(B\), l’événement qui est réalisé si et seulement si \(A\) et \(B\) le sont. Il est donc constitué des éventualités appartenant à la fois à \(A\) et \(B\).
C’est un événement noté \(A \cap B\) tel que : \(\forall A,B \in \varepsilon{(\Omega)}, A \cap B \in \varepsilon(\Omega)\) avec \(\omega \in A \cap B \Leftrightarrow (\omega \in A \ \text{et} \ \omega \in B)\)
L’intersection \(A \cap B\) correspond à la conjonction logique « \(A\) et \(B\) ».
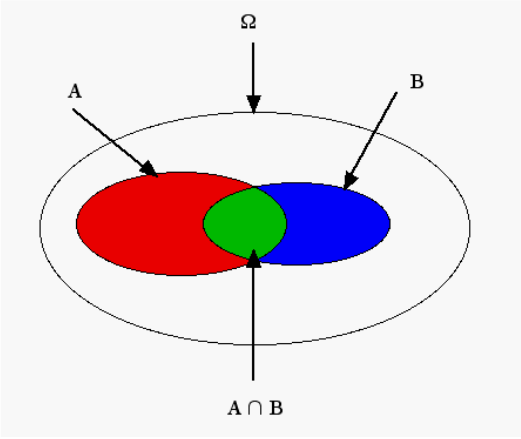
L’intersection des deux évènements \(A\) et \(B\) figure en vert sur le graphe ci-contre.
Remarque : L’univers des possibles \(\Omega\) n’étant pas limité uniquement aux évènements \(A\) (parties rouge et verte) et \(B\) (parties bleu et verte), l’événement complémentaire \(\bar{A}\),est formé des parties bleu et blanche.
Exemple:
Dans l’exemple concernant les groupes sanguins, si à l’événement \(A\) « l’individu est de rhésus positif » , on ajoute l’événement \(B\) « l’individu possède l’allèle B », l’intersection de ces deux évènements donne : \(A \cap B = \{\text{B+, AB+}\}\)
Deux évènements \(A\) et \(B\) sont incompatibles ou disjoints, s’ils ne peuvent être réalisés simultanément. On a alors : \(A \cap B = \emptyset\)
Quelques propriétés de l’intersection \((\cap)\) :
\(A \cap \bar{A} = \emptyset\) évènements incompatibles
\(\Omega \cap A = A\) élément neutre \((\Omega)\)
\(\emptyset \cap A = \emptyset\) élément absorbant \((\emptyset)\)
\(A \cap B = B \cap A\) commutativité
\(A \cap ( B \cap C) = (A \cap B) \cap C\) associativité
\(A \cap ( B \cap C) = (A \cap B) \cup (A \cap C)\) distributivité avec la réunion \((\cup)\)
2.3.2. La réunion de deux évènements
On appelle réunion de deux évènements \(A\) et \(B\), l’événement qui est réalisé si et seulement si \(A\) ou \(B\) est réalisé. Il est donc constitué des éventualités appartenant à \(A\) ou \(B\).
C’est un événement noté \(A \cup B\) tel que :
\(\forall A,B \in \varepsilon{(\Omega)}, A \cup B \in \varepsilon{(\Omega)}\)
avec \(\omega \in A \cup B \Leftrightarrow (\omega \in A \ \text{ou} \ \omega \in B)\)
La réunion \(A \cup B\) correspond à la disjonction logique « \(A\) ou \(B\) ».
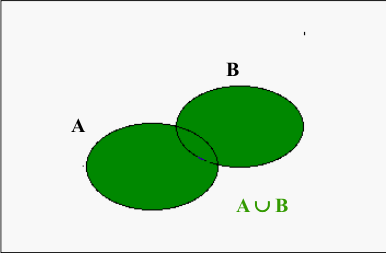
La réunion des deux évènements \(A\) et \(B\) figure en vert sur le graphe ci-contre.
Remarque : La réunion de deux évènements n’est pas la somme algébrique des évènements dans la mesure où la zone de recouvrement n’est pas comptabilisée deux fois.
Exemple : Dans l’exemple concernant les groupes sanguins, si à l’événement \(A\) « l’individu est de rhésus positif », on ajoute l’événement \(B\) « l’individu possède l’allèle B », la réunion de ces deux évènements donne : \(A \cup B = \{\text{A+,B+,B-,AB+,AB-,O+}\}\)
Quelques propriétés de la réunion \((\cup)\):
\(A \cup \bar{A} = \Omega\) évènements complémentaires
\(\emptyset \cup A = A\) élément neutre \((\emptyset)\)
\(\Omega \cup A = \Omega\) élément absorbant \((\Omega)\)
\(A \cup B = B \cup A\) commutativité
\(A \cup ( B \cup C) = (A \cup B) \cup C\) associativité
\(A \cup ( B \cap C) = (A \cup B) \cap (A \cup C)\) distributivité avec la intersection \((\cap)\)
Selon les lois de Morgan, nous avons :
\(\bar{A \cap B} = \bar{A} \cup \bar{B}\) ce qui correspond à la partie hachurée sur ce graphe.
\(\bar {A \cup B} = \bar{A} \cap \bar{B}\) ce qui correspond à l’ensemble vide \(\emptyset\) lorsque l’univers des possibles \(\Omega\) n’est constitué que des évènements \(A\) et \(B\) (graphe).
2.3.3. L’inclusion d’un événement
Un événement \(A\) entraîne un événement \(B\) si la réalisation de \(A\) implique celle de \(B\). On dit que l’événement \(A\) est inclus dans l’événement \(B\).
\(A \subset B\)
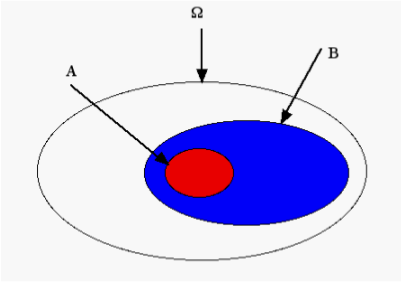
L’implication logique « \(A \Rightarrow B\) » se traduit par l’inclusion \(A \subset B\).
Exemple de l’inclusion de l’événement \(A\) en rouge dans l’événement \(B\) en bleu.
Exemple :
Soit une urne contenant des billes rouges unies et des billes vertes unies et striées. Si l’on note \(A\) l’événement « obtention d’une bille striée » et \(B\) l’événement « obtention d’une bille verte », la réalisation de \(A\) implique la réalisation de \(B\) car \(A\) est inclus dans \(B\).
2.4. Système complet d’évènements
\({A_1},{A_2},.....,{A_n}\) forment un système complet d’évènements si les parties \({A_1},{A_2},.....,{A_n}\) de \(\Omega\) constituent une partition de \(\Omega\) telle que :
\(\forall i \qquad {A_i} \ne \emptyset\)
\(\forall i \ne j \quad {A_i} \cap {A_j} = \emptyset\)
\(\bigcup\limits_i {A_i} = \Omega\)
Un système complet d’évènements est formé de toutes les parties de \(\Omega\), c’est-à-dire des familles d’évènements 2 à 2 incompatibles dont la réunion constitue l’événement certain \(\Omega\).
Le nombre de partitions possibles dans un ensemble fini de \(n\) évènements est : si \(\text{Card}(\Omega) = n\) alors \(\text{Card}\ \mathcal{P}(\Omega) = 2^n\)
Voir Illustration
2.5. Espace probabilisable
Supposons que l’ensemble des évènements constitue une classe \(\mathcal{C}\) de \(\mathcal{P}{(\Omega)}\) , telle que :
\(\mathcal{C} \subseteq \mathcal{P}{(\Omega)}\)
On appelle espace probabilisable \((\Omega,\mathcal{C})\), un objet formé de deux éléments :
un espace d’éventualités \((\Omega)\)
un espace d’évènements \(\mathcal(C) \subseteq \mathcal {P}{(\Omega)}\)
avec :
\((P_1) \qquad A \in \mathcal(C) \Rightarrow \bar{A} \in \mathcal{C}\)
\((P_2) \qquad A_i \in \mathcal(C) \ (\forall i \in \mathbb{N^*}) \Rightarrow \bigcup\limits_i \bar{A_i} \in \mathcal{C}\)
\((P_3) \qquad \Omega \in \mathcal{C}\)
<>
Ces trois axiomes ou propriétés suffisent à définir un espace probabilisable et on pourrait montrer qu’il implique que \(\emptyset \in \mathcal{C} \ \text{et} \ \bigcap\limits_i A_i \in \mathcal{C}\)
3. Probabilités
Le passage d’une description de type ensembliste des phénomènes aléatoires à l’élaboration d’un véritable modèle mathématique se fait en introduisant les mesures de probabilité.
3.1 Définitions
3.1.1 Concept mathématique
On appelle probabilité \(P\) toute application de l’ensemble des évènements \(\Omega\) dans l’intervalle \([0,1]\), tel que :
\(P: \qquad \varepsilon(\Omega) \rightarrow [0,1]\)
\(A \mapsto P(A)\)
satisfaisant les propriétés (ou axiomes) suivantes
\((P_1) \qquad \forall(A) \in \varepsilon(\Omega) \qquad P(A) \geq 0\)
\((P_2) \qquad P(\Omega)=1\)
\((P_3) \qquad \forall A,B \in \varepsilon (\Omega) \quad \text{si} \quad A \cap B = \emptyset \quad \text{alors} \quad P( A \cup B)=P(A) + P(B)\)
Remarque : Le concept mathématique de probabilité modélise les notions intuitives de proportion et de fréquence. Si l’on avance que la probabilité d’être immunisé contre la tuberculose est de 0,8, on modélise le fait qu’environ 80 % de la population est immunisé contre la tuberculose.
3.1.2. Probabilités combinatoires
Soit \(\Omega\) un espace fondamental fini constitué de \(N\) évènements élémentaires sur lequel on fait l’hypothèse d’équiprobabilité de réalisation des \(N\) évènements élémentaires. On suppose ainsi que tous les évènements élémentaires ont « la même chance » de se réaliser. Dans ce cas la probabilité \(p_i\) d’un événement élémentaire quelconque \(\omega_I\) est telle que :
\({p_i} = \frac{1}{N} \quad \text{avec} \quad p_i = P(\omega_I)\)
satisfaisant:
\((P_1) \ \text{avec} \ \forall I \ p_i \geq 0\)
\((P_2) \ \sum_i p_i = 1\)
Soit \(A\) un événement quelconque constitué de k évènements élémentaires de , on en déduit :
\(P(A) = \frac{k}{N} \qquad \text{avec} \qquad P(A) = \sum\limits_{\omega_i \in A} {p_i}\)
Cette formule s’énonce souvent comme :
\(P(A) = \frac{\text{card}\ A}{\text{card}\ \Omega} = \frac{\text{nombre de cas favorables}} {\text{nombre de cas possibles}}\)
Cette formule permet de ramener les calculs de probabilités à des décomptes d’évènements élémentaires effectués par des techniques d’analyse combinatoire qui ne sont pas des probabilités.
Exemples :
En tapant 5 lettres au hasard sur une machine à écrire (possibilité de taper plusieurs fois sur la même touche), la probabilité d’obtenir le mot « lutte » est d’une chance sur 12 millions. En effet il y a exactement 11 881 376 mots de 5 lettres possibles (?theme=proba&chap=1#Arrangement avec répétitions) avec répétition).
La probabilité d’obtenir un multiple de trois lors du lancé d’un dé à 6 faces, non pipé est : \(A = \{3,6\}\) d’où \(P(A) = 2/6\) \(=1/3\) avec \(k=2\) et \(p_i=1/6\)
3.1.3. Loi des grands nombres
Si l’on répète \(N\) fois une expérience dans laquelle la probabilité d’apparition d’un événement \(A\) est \(P\), la fréquence de cet événement au cours des \(N\) expériences, \(\frac{k}{N}\) tend vers \(P\) lorsque \(N\) tend vers l’infini. \(N \to \infty \Rightarrow \frac{k}{N} \to P\)
Lorsque le nombre d’épreuves augmente indéfiniment, les fréquences observées tendent vers les probabilités et les distributions observées vers les lois de probabilité.
Exemple:
Lors d’un croisement entre plantes hétérozygotes Aa pour un caractère à dominance stricte (allèle A, forme sauvage et allèle a, forme mutée), on examine successivement deux échantillons de plantes résultant de ce croisement.
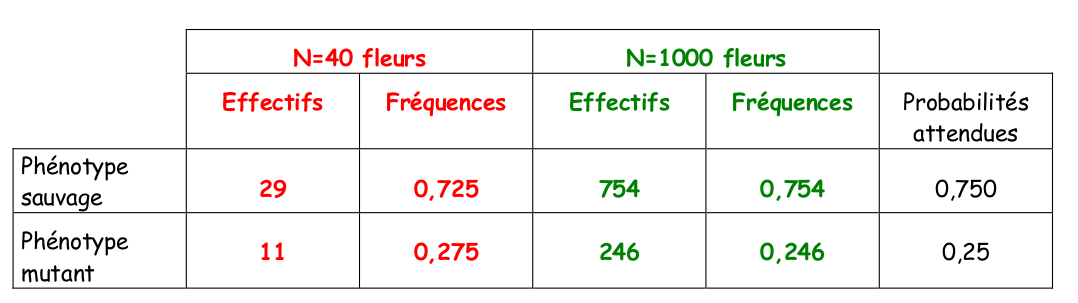
Il est aisé de vérifier que les fréquences pour les deux phénotypes possibles sont plus proches des probabilités attendues sous le modèle de croisement mendélien pour l’échantillon de très grande taille. L’écart entre les fréquences observées et les probabilités attendues peut être tester à l’aide du test du khi-deux.
3.1.4. Espace probabilisé
Nous définirons un espace probabilisé en utilisant l’axiomatique de Kolmogorov,
Définition 1 :
On appelle probabilité sur \((\Omega,\mathcal{C})\) une application \(P\) de \(\mathcal{C}\) dans l’intervalle \([0,1]\) telle que :
- \(P(\Omega)=1\)
- Pour tout ensemble dénombrable d’évènements incompatibles 2 à 2, on a : \(P(\bigcup\limits_i {A_i}) = \sum\limits_{i = 1}^n {P({A_i})}\)
Définition 2 :
On appelle espace probabilisé, le triplet \((\Omega,\mathcal{C},P)\)
<>
Ainsi un espace probabilisé désigne un espace fondamental et ses évènements, muni d’une mesure de probabilités.
3.2 Propriétés des probabilités
Des axiomes précédents découlent les propriétés additives des probabilités, d’usage permanent.
3.2.1. Additivité
- Cas d’évènements incompatibles
Si \(A_1,A_2,...,A_i,...,A_n\) sont \(n\) évènements incompatibles deux à deux (\(A_i \cap A_j = \emptyset \quad \text{si} \quad i \neq j\)) alors : \(P( A_1 \cup A_2 \cup ... \cup A_i \cup ... \cup A_n ) = P(A_1) + P(A_2) + ... + P(A_i) + ... + P(A_n)\)
La probabilité de la réunion d’un ensemble fini ou dénombrable d’évènements
2 à 2 incompatibles est égale à la somme de leur probabilité d’où :
\(P(\bigcup\limits_i {A_i} ) = \sum\limits_{i = 1}^n {P({A_i})}\)
voir Démonstration
- Cas de deux évènements quelconques
Si \(A\) et \(B\) sont deux évènements quelconques, alors :
\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
Voici pourquoi :
\(A\) et \(B\) étant deux évènements quelconques, \((A \cap B) \neq \emptyset\) , ces évènements peuvent se décomposer comme la réunion de deux évènements incompatibles :
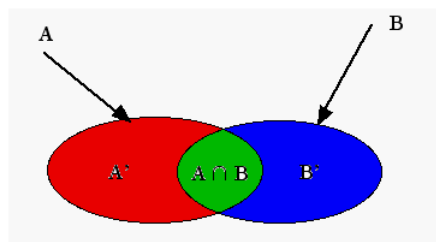
Alors :
- \(A = {A}' \cup (A \cap B)\) avec \({A}' \cap (A \cap B) = \emptyset\)
alors \(P(A) = P({A}') + P(A \cap B)\)
et \(P({A}') = P(A) - P(A \cap B)\)
- \(B = {B}' \cup (A \cap B)\) avec \({B}' \cap (A \cap B) = \emptyset\)
d’où \(P({B}') = P(B) - P(A \cap B)\)
- \(P(A \cup B) = P({A}') + P(A \cap B) + P({B}')\)
d’où \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
Exemple :
Dans l’exemple du lancer d’un dé à 6 faces, non pipé, on considère l’événement \(A\) « le résultat est pair » et l’événement \(B\) « le résultat est un multiple de trois ».
On a alors :
\(A = \{2,4,6\}\) et \(B = \{3,6\}\) donc \(A \cup B = \{2,3,4,6\}\) et \(A \cap B = \{6\}\)
avec \(P(A) = 3/6 \quad P(B) = 2/6 \quad P(A \cup B ) = 4/6 \quad P(A \cap B ) = 1/6\)
on vérifie alors que : \(P(A \cup B) = P(A) + P(B) - P(A \cap B) = 3/6 + 2/6 - 1/6 = 4/6\)
3.2.2 Evènement contraire
Si \(A\) est un événement quelconque, alors \(P(\bar{A)}= 1 - P(A)\)
Voici pourquoi :
Nous avons vu précédemment que
\(A \cup \bar{A} = \Omega \quad \text{et} A \cap \bar{A} = \emptyset\) Propriétés de la réunion et de intersection
\(P(A \cup \bar{A}) = P(A) + P(\bar{A})\) Propriétés d’additivité des probabilités
d’où \(P(\Omega) = 1 = P(A) + P(\bar{A})\) ainsi \(P(\bar{A}) = 1 - P(A)\)
Exemple: La probabilité lors du lancer d’un dé non pipé d’obtenir « plus de 2 » se traduit par \(A = \{3,4,5,6\}\) et \(A = \{1,2\}\) d’où \(P ( A ) = 1 – P ( A ) = 1 – 2/6 = 4/6 = 2/3\)
Remarque: L’application de cette propriété est très utile lorsque le nombre d’évènements élémentaires de A , k , est important et que le calcul des probabilités p i est fastidieux (?theme=proba&chap=3#Loi de Poisson)).
3.2.3 Evènement impossible
\(P (\emptyset) = 0\)
Voici pourquoi:
Nous avons vu précédemment que \(\emptyset \cup \Omega = \Omega\) élément neutre
\(P (\emptyset \cup \Omega) = P (\emptyset) + P (\Omega)\) Propriétés d’additivité des probabilités
d’où \(P (\Omega) = P (\emptyset) + P (\Omega)\) ainsi \(P (\emptyset) = 0\)
3.2.4 Inclusion
Si \(A \subset B\) alors \(P ( A ) \leq P ( B )\)
Voici pourquoi :
si \(B = {B}’ \cup A\) avec \(B ’ \cap A = \emptyset\)
alors \(P ( B )= P ( B ’ \cup A ) = P ( B ’) + P ( A )\)
d’où \(P ( A ) \leq P ( B )\)
avec \(P ( A ) = P ( B )\) lorsque \(P ( B ’) = 0\)
3.3 Indépendance statistique
3.3.1 Définition
L’hypothèse d’indépendance entre évènements et plus généralement entre épreuves successives est un préalable lors de l’établissement des lois de probabilités
On dit que deux évènements A et B sont indépendants si l’on a :
\(P ( A \cap B ) = P ( A ) P ( B )\)
Ainsi si A et B sont deux évènements statistiquement indépendants, la probabilité de la réalisation conjointe de ces deux évènements est le produit de leur probabilité respective.
Remarque :
Il ne faut pas confondre évènements indépendants et évènements incompatibles.
Supposons A et B à la fois indépendants et incompatibles. On a alors :
\(P ( A \cap B ) = P ( A ) P ( B )\) indépendants
\(P ( A \cap B ) = P (\emptyset) = 0\) incompatibles
d’où nécessairement \(P ( A ) = 0\) ou \(P ( B ) = 0\)
Exemples :
- Dans l’exemple du lancer d’un dé à 6 faces, non pipé, les deux évènements : A « le résultat est pair » et B « le résultat est un multiple de trois » sont statistiquement indépendants.
En effet, soit \(A = \{2,4,6\} \quad B = \{3,6\} \quad A \cap B = \{6\}\) ainsi \(P ( A ) = 3/6 \quad P ( B ) = 2/6 \quad P ( A \cap B ) =\) \(1/6\) on vérifie alors que : \(P ( A \cap B ) = P ( A ) P ( B ) = (3/6) \times (2/6) = 6/36 =\) \(1/6\)
- Si l’on considère une famille de deux enfants, les deux évènements : A « enfants de sexe différent » et B « au plus une fille » ne sont pas statistiquement indépendants.
En effet, l’espace probabilisé \(\Omega\), contient 4 évènements élémentaires (si l’on considère une famille ordonnée),
\(\Omega = A \cup B = \{GG, GF, FG, FF\}\)
avec \(A = \{GF, FG\}\), \(B = \{GG, GF, FG\}\) et \(A \cap B = \{GF, FG\}\)
d’où sous l’hypothèse d’équiprobabilité : \(P ( A ) = 1/2\), \(P ( B ) = 3/4\) et \(P ( A \cap B ) =\) \(1/2\)
On vérifie alors que : \(P ( A \cap B ) \neq P ( A ) P ( B ) = (1/2) \times (3/4) =\) \(3/8\) \(\quad \neq\) \(1/2\)
3.3.2 Propriétés
Les propriétés associées à l’indépendance sont :
- si \(A\) est un évènement quelconque,
\(A\) et \(\Omega\) sont indépendants : \(A \cap \Omega = A\) élément neutre
\(P ( A \cap \Omega) = P ( A ) P (\Omega) = P ( A )\) car \(P (\Omega) = 1\)
\(A\) et \(ø\) sont indépendants : \(A \cap \emptyset = \emptyset\) élément absorbant
\(P ( A \cap \emptyset) = P ( A ) P (\emptyset) = P (\emptyset)\) car \(P (\emptyset) = 0\)
- si A et B sont deux évènements quelconques,
\(A\) et \(B\) sont indépendants si et seulement si \(A\) et \(\bar{B}\) ou (\(\bar{A}\) et \(B\)) sont indépendants (démonstration).
\(A\) et \(B\) sont indépendants si et seulement si \(\bar{A}\) et \(\bar{B}\) le sont.
3.3.3 Généralisation à n évènements
\(n\) évènements \(( n \geq 2)\), \(A_1 , A_2 ,..., A_i ,.., A_n\) sont dit indépendants dans leur ensemble (ou mutuellement indépendants) si on a : \(P ( A_1 \cap A_2 \cap...\cap A_i \cap... \cap A_n ) = P ( A_1 ) \times P ( A_2 ) \times ...\times P ( A_i ) \times....\times P ( A_n )\)
\(P(\bigcap\limits_i {A_i} ) = \prod\limits_{i = 1}^n {{A_i}}\)
Remarque :
\(n\) évènements peuvent être indépendants deux à deux,
\([ P ( A_i \cap A_j ) = P ( A_i ) x P ( A_j )]\) avec \(i \neq j\) sans être indépendants au sens de la définition ci-dessus.
Exemple :
On jette deux dés non pipés et on considère les évènements suivants :
\(A_1\) « le premier dé donne un nombre pair »
\(A_2\) « le deuxième dé donne un nombre pair »
\(A_3\) « la somme des deux lancers est paire »
Le nombre d’événements élémentaires est :
\(\text{card} (\Omega)=\) \(36\) (?theme=proba&chap=1#Arrangements avec répétitions) avec \(p= 2\) et \(n= 6\))
Les 3 évènements \(A_1\), \(A_2\) et \(A_3\) sont 2 à 2 indépendants mais ne sont pas indépendants dans leur ensemble. En effet :
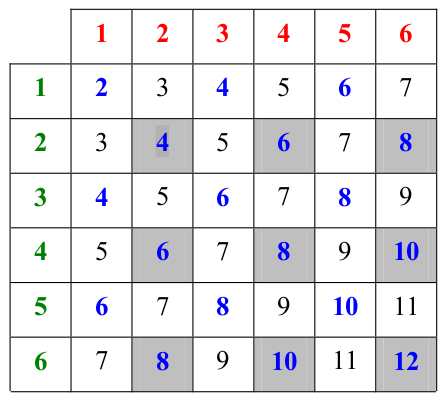
Les probabilités associées aux 3 évènements sont :
\(P ( A_1 )= 1/2\) ; \(P ( A_2 )=1/2\) ; \(P ( A_3 )=1/2\)
\(P ( A_1 \cap A_2 ) = 9/36 = 1/4 = P ( A_1 ) P ( A_2 )\)
\(P ( A_1 \cap A_3 ) = 9/36 = 1/4 = P ( A_1 ) P ( A_3 )\)
\(P ( A_2 \cap A_3 ) = 9/36 = 1/4 = P ( A_2 ) P ( A_3 )\)
\(P ( A_1 \cap A_2 \cap A_3 ) = 9/36 = 1/4 \qquad \neq P ( A_1 ) P ( A_2 ) P ( A_3 ) = 1/8\)
Les cases grisées représentent les évènements élémentaires réalisés dans le cadre soit \(A_1 \cap A_2\) ou \(A_1 \cap A_3\) ou \(A_2 \cap A_3\) ou \(A_1 \cap A_2 \cap A_3\).
4. Probabilités conditionnelles
4.1. Définition
Soit deux évènements \(A\) et \(B\) d’un espace probabilisé \(\Omega\) avec \(P ( B )\neq 0\), on appelle probabilité conditionnelle de l’évènement « \(A\) si \(B\)» (ou « \(A\) sachant \(B\) »), le quotient
\(P(A/B) = \frac{P(A \cap B)}{P(B)}\) notée \(P_B ( A )\)
On définit ainsi une probabilité sur \(\Omega\) au sens de la définition donnée précédemment.
Théorème :
Soit B un évènement de probabilité non nulle, alors :
\(P B : \varepsilon (\Omega) → [0,1]\)
\(A \mapsto P(A/B) = \frac{P(A \cap B)}{P(B)}\) est une probabilité sur \(\Omega\)
Voici pourquoi :
(\(P_1\)) \(\forall A \in \varepsilon (\Omega) \qquad P ( A \mid B ) \geq 0\) (quotient de deux réels positifs)
(\(P_2\)) \(P (\Omega \mid B ) = \frac{P(\Omega \cap B)}{P(B)} = \frac{P(B)}{P(B)} = 1\) car \(\Omega \cap B = B\) car \(\Omega\) élément neutre
(\(P_3\)) si \(( A_1 \cap A_2 )=\emptyset\), \(P_B ( A_1 \cup A_2 ) = \frac{P[(A_1 \cup A_2 ) \cap B]}{P(B)} = \frac{P[(A_1 \cap B) \cup (A_2 \cap B)]}{P(B)} = \frac{P[(A 1 \cap B) + (A 2 \cap B)]}{P(B)} = P_B ( A_1 ) + P_B ( A_2 )\) additivité indépendants
Remarque : La probabilité \(P ( A )\) est appelée la probabilité a priori et \(P ( A | B )\) ou \(P_B ( A )\) la probabilité a posteriori car sa réalisation dépend de la réalisation de \(B\).
On observe les relations suivantes :
\(P ( A \mid A )=1\)
Si \(B \subset A\) , alors \(A \cap B = B\) et donc \(P ( B \mid A ) = \frac{P ( B )}{P ( A )}\)
Exemple :
Soit un croisement entre hétérozygotes Aa pour un caractère à dominance stricte, quelle est la probabilité d’obtenir à la génération suivante parmi les individus de phénotype A, un individu homozygote ?
L’ensemble des évènements élémentaires est : \(\Omega = \{AA,Aa,aA,aa\}\) Si \(h =\) homozygote et \(\bar{h} =\) hétérozygote
\(P(h \mid A ) = \frac{P(h \cap A)}{P(A)} = \frac{1/4}{3/4} =\) \(1/3\) probabilité a posteriori
La probabilité a priori d’obtenir un homozygote est 1/4.
4.2. Probabilités composées
Théorème :
Soit deux évènements A et B d’un espace probabilisé . Alors,
\(P(A \cap B) = P(B \mid A) P(A) = P(A \mid B) P(B)\) Formule des probabilités composées
Voici pourquoi:
Par définition, \(P ( A \mid B ) = \frac{P ( A \cap B )}{P ( B )}\) d’où \(P(A \cap B) = P(A \mid B) P(B)\)
Par symétrie, \(P(A \cap B) = P(A \mid B) P(B) = P(B \mid A) P(A)\)
Si A et B sont deux évènements indépendants et que \(P(B)\neq 0\) alors ceci équivaut à affirmer que
\(P_B (A) = P(A \mid B) = P(A)\)
Lorsque deux évènements sont indépendants , le fait que l’un des évènements soit réalisé, n’apporte aucune information sur la réalisation de l’autre. Dans ce cas la probabilité conditionnelle \(P_B (A)\) (a posteriori ) est égale à la probabilité \(P(A)\) (a priori).
Voici pourquoi :
La formule des probabilités composées donne \(P(A \cap B) = P(A \mid B) P(B)\)
L’indépendance statistique entre A et B équivaut à \(P(A \cap B) = P(A) P(B)\)
d’où la relation \(P(A \mid B) = P(A)\)
Si A et B sont deux évènements indépendants alors ceci équivaut à affirmer que \(P_B (A) = P_{\bar{B}} (A) = P(A)\)
Lorsque deux évènements sont indépendants , la probabilité conditionnelle de \(A\) est la même que ce soit \(B\) ou \(B\) qui est réalisé (voir démonstration).
Dans l’exemple du lancer d’un dé à 6 faces, non pipé, les deux évènements : \(A\) « le résultat est pair » et \(B\) « le résultat est un multiple de trois » sont indépendants ( voir exemple ). Ainsi la probabilité que la face soit paire sachant que c’est un multiple de 3 est :
si \(A = \{2,4,6\} \quad B =\{3,6\} \quad A \cap B=\{6\}\)
et \(P(A)=3/6 \quad P(B)=2/6 \quad P(A \cap B)=1/6\)
\(P ( A \mid B ) = \frac{P ( A \cap B )}{P ( B )} = \frac{1/6}{1/3} =\) \(1/2\) = \(P ( A )\) d’où la relation \(P(A \mid B) = P(A)\)
4.3. Probabilités totales
Théorème :
Si \(\{A_1 , A_2 ,....,A_i ,.....,A_n \}\) est un système complet d’évènements , quel que soit l’évènement \(B\), alors : \(P(B) = P(B \mid A_1 )P(A_1 ) + P(B \mid A_2 )P(A_2 )+.....+ P(B \mid A_n )P(A_n )\)
\(P ( B ) = \sum\limits_{i=1}^{n} P ( B \mid A_i ) P ( A_i )\) Formule des probabilités totales
Voici pourquoi :
Si \(i \neq j\), alors \((A_i \cap B) \cap (A_j \cap B) = (A_i \cap A_j )\cap B = \emptyset\)
Grâce à la distributivité , on a :
\((A_1 \cap B)\cup (A_2 \cap B) \cup......\cup (A_n \cap B) = (A_1 \cup A_2 \cup....\cup A_n ) \cap B = \Omega \cap B = B\)
Grâce à l ’additivité , on a :
\(P(B) =P(A_1 \cap B) + P(A_2 \cap B) + ......+ P(A_n \cap B)\)
Grâce à la formule des probabilités composées , on a :
\(P(A_1 \cap B) = P(B \mid A_1 ) P( A_1 )\)
d’où \(P(B)= P(B \mid A_1 )P(A_1 ) + P(B \mid A_2 )P(A_2 )+.....+ P(B \mid A_n )P(A_n )\)
Exemple :
Une population animale comporte 1/3 de mâles et 2/3 de femelles. L’albinisme frappe 6 % des mâles et 0,36 % des femelles. La probabilité pour qu’un individu pris au hasard (dont on ignore le sexe) soit albinos est :
Si \(A\) = {mâle} et \(\bar A\) = {femelle} constitue un système complet d’évènements
\(B\) = {albinos} et \(\bar B\) = {non albinos}
sachant que \(P(B) = P(B \mid A) P(A) + P(B \mid \bar{A} )P( \bar{A} )\)
alors \(P(B) = (0,06 \times 1/3) + (0,0036 \times 2/3) =\) 0,0224
soit 2,24% d’albinos dans cette population.
4.4. Le théorème de Bayes
Un corollaire au théorème des probabilités totales est connu sous le nom de formule de Bayes.
Théorème :
Si \(\{A_1 , A_2 ,....,A_i ,.....,A_n \}\) est un système complet d’évènements , et quel que soit l’évènement \(B\) tel que \(P(B) \neq 0\), alors :
\(P ( A_i \mid B ) = \frac{ P ( B \mid A_i ) P ( A_i ) }{ P ( B \mid A_1 ) P ( A_1 ) + ... + P ( B \mid A_i ) P ( A_i ) + ... + P ( B \mid A_n ) P ( A_n ) }\)
\(P ( A_i \mid B ) = \frac{ P ( B \mid A_i ) P ( A_i ) }{ \sum\limits_{i=1}^{n} P ( B \mid A_i ) P ( A_i )}\) Formule de Bayes
Voici pourquoi :
D’après la formule des probabilités composées,
\(P({A_i} \cap B) = P({A_i}\mid B) P(B) = P(B \mid{A_i} )P({A_i})\)
D’après la formule des probabilités totales,
\(P(B) = \sum\limits_{i = 1}^n {P(B} \mid {A_i})P({A_i})\)
D’après la formule des probabilités conditionnelles,
\(P({A_i} \mid B) = \frac{{P({A_i} \cap B)}}{{P(B)}}\)
d’où \(P( A_i \mid B) = \frac{ P ( B \mid A_i ) P ( A_i ) }{ \sum\limits_{i = 1}^n P ( B \mid A_i ) P ( A_i ) }\)
Remarque :
La formule de Bayes est utilisée de façon classique pour calculer des probabilités de causes dans des diagnostics (maladies, pannes, etc.). L’application du théorème de Bayes est à la base de toute une branche de la statistique appeléestatistique bayesienne.
Exemple :
Dans une population pour laquelle 1 habitant sur 100 est atteint d’une maladie génétique A, on a mis au point un test de dépistage. Le résultat du test est soit positif (\(T\)) soit négatif (\(\bar{T}\)). On sait que : \(P(T \mid A) = 0,8\) et \(P(\bar{T} \mid \bar{A} ) = 0,9\)
On soumet un patient au test. Celui-ci est positif. Quelle est la probabilité que ce patient soit atteint de la maladie A soit \(P_{T}(A)\) ou P(A T)?
D’après la formule de Bayes :
\(P (A \mid T) = \frac{ P(A \cap T) } { P(T) } = \frac{ P(T \mid A) P(A) }{ P ( T \mid A ) P ( A ) + P ( T \mid \bar{A} ) P( \bar{A})}\)
d’où \(P(A/T) = \frac{ 0,01 \times 0,8 }{ 0,8 \times 0,01 + 0,1 \times 0,99} =\) \(0,075\)
Ainsi avant le test, la probabilité d’être malade était de \(P(A) =\) 0 ,01 (probabilité a priori)
et après le test la probabilité d’être malade est de \(P(A \mid T) =\) 0,075 (probabilité a posteriori).
Ainsi le test apporte un supplément d’information.