Chapitre 1 — Analyse combinatoire

1. Introduction
L’analyse combinatoire est une branche des mathématiques qui étudie comment compter les objets. Elle fournit des méthodes de dénombrements particulièrement utiles en théorie des probabilités. Les probabilités dites combinatoires utilisent constamment les formules de l’analyse combinatoire développées dans ce chapitre. Un exemple des applications intéressantes de cette dernière est la démonstration du développement du binôme de Newtonutilisé dans le calcul des probabilités d’une loi binomiale.
2. Arrangements
2.1. Définition
Etant donné un ensemble E de n objets, on appelle arrangements de p objets toutes suites ordonnées de p objets pris parmi les n objets. Le nombre d’arrangements de p objets pris parmi n est noté : \(A_n^p\).
Remarque : On a nécessairement \(1 \geq p \geq n\) et \(n, p \in N\) Si \(n < p\), alors \(A_n^p\)
Deux arrangements de \(p\) objets sont donc distincts s’ils diffèrent par la nature des objets qui les composent ou par leur ordre dans la suite.
Exemples :
Une séquence d’ADN est constituée d’un enchaînement de 4 nucléotides [A (Adénine), C (Cytosine), G (Guanine) et T (Thymine)]. Il existe différents arrangements possibles de deux nucléotides ou dinucléotides avec \(p\)=2 et \(n\)=4.
Le nombre de mots de 5 lettres (avec ou sans signification) formés avec les 26 lettres de l’alphabet correspond au nombre d’arrangements possibles avec \(p\)=5 et \(n\)=26.
Le tiercé dans l’ordre lors d’une course de 20 chevaux constitue un des arrangements possibles avec \(p\)=3 et \(n\)=20.
Dans les exemples précédents, l’ordre des éléments dans la suite est essentiel. Ainsi pour le deuxième exemple, le mot NICHE est différent du mot CHIEN.
Mais dans les deux premiers exemples, une base ou une lettre de l’alphabet peut se retrouver plusieurs fois alors que dans le troisième exemple, les trois chevaux à l’arrivée sont forcément différents. Il faut donc distinguer le nombre d’arrangements avec répétition et le nombre d’arrangements sans répétition (arrangements au sens strict).
2.2. Arrangements avec répétitions
Lorsqu’un objet peut être observé plusieurs fois dans un arrangement, le nombre d’arrangement avec répétition de \(p\) objets pris parmi \(n\), est alors :
\(A_n^p = {n^p} \qquad avec \qquad 1 \geq p \geq n\)
Voici pourquoi :
Pour le premier objet tiré, il existe \(n\) manières de ranger l’objet parmi \(n\).
Pour le second objet tiré, il existe également \(n\) possibilités d’arrangements car le premier objet fait de nouveau parti des \(n\) objets. On parle de tirage avec remise.
Ainsi pour les \(p\) objets tirés, il y aura \(n \times n \times n \times n \times … \times n\) (\(p\) fois) arrangements possibles, soit \(A_n^p = n \times n \times n \times .... \times n = {n^p}\)
Exemples :
- Concernant l’exemple de la séquence d’ADN, le nombre de dinucléotides attendus si l’on fait l’hypothèse qu’une base peut être observée plusieurs fois dans la séquence (ce qui correspond effectivement à la réalité) est donc : \(A_4^2\) = \(4^2\) = 16 dinucléotides possibles
Les 16 dinucléotides identifiables dans une séquence d’ADN sont :
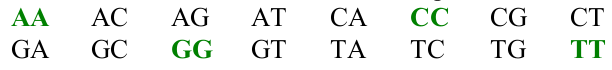
2.3.1 Arrangements sans répétition
Lorsque chaque objet ne peut être observé qu’une seule fois dans un arrangement, le nombre d’arrangements sans répétition de p objets pris parmi \(n\) est alors : \(A_n^p = \frac{{n!}}{{(n - p)!}} \text{ avec } 1 \geq p \geq n\)
Voici pourquoi : Pour le premier objet tiré, il y a \(n\) manières de ranger l’objet parmi \(n\).
Pour le second objet tiré, il n’existe plus que n-1 manières de ranger l’objet car le premier objet ne peut plus être pris en compte. On parle de tirage sans remise.
Ainsi pour les \(p\) objets tirés parmi \(n\), si \(1 \geq p \geq n\), il y aura : \(A_n^p = n(n - 1)(n - 2)....(n - p + 1)\) (\(p\) produits)
de plus \(A_n^p = n(n - 1)(n - 2)....(n - p + 1) \frac{(n - p) \times ....\times 2 \times 1}{(n - p) \times .... \times 2 \times 1}\)
d’où \(A_n^p = \frac{{n!}}{{(n - p)!}}\)
Rappel : Si \(n \in N^*\) , on appelle factorielle \(n\), notée \(n!\) , le produit des \(n\) premiers entiers : \(1 \times 2 \times 3 \times ..... \times p \times (p + 1) \times ...\times (n - 1) \times n = n!\)
\(0! = 1\) par convention car \(0!\) n’est en principe pas définie.
Dès que \(n\) dépasse la dizaine, \(n!\) se compte en millions. Il est bon de connaître la formule d’approximation suivante (« formule de Stirling »):
\(n! \approx {\left( {\frac{n}{e}} \right)^n}\sqrt {2\pi n}\)
Exemple:
Concernant l’exemple de la séquence d’ADN, le nombre de dinucléotides attendu dans une séquence si l’on fait l’hypothèse qu’une base n’est observée qu’une seule fois est donc : \(A_4^2\) = \(\frac{4!}{(4 - 2)!}\) = 12 dinucléotides possibles
Sous cette contrainte, les 12 dinucléotides possibles sont :
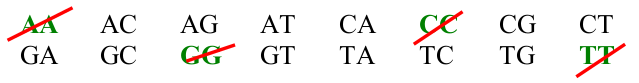
Ceci correspond aux 16 arrangements possibles avec répétition (\(A_n^p = {n^p}\)) auxquels sont soustraits les 4 dinucléotides (\(n\)) résultant de l’association d’une même base.
3. Permutations
3.1. Permutations sans répétition
Etant donné un ensemble \(E\) de \(n\) objets, on appelle permutations de \(n\) objets distincts toutes suites ordonnées de \(n\) objets ou tout arrangement \(n\) à \(n\) de ces objets. Le nombre de permutations de \(n\) objets est noté : \(P_n = n!\)
La permutation de \(n\) objets constitue un cas particulier d’arrangement sans répétition de \(p\) objets pris parmi \(n\) lorsque \(p = n\)
Ainsi le nombre de permutations de \(n\) objets est : \(A_n^n = \frac{n!}{(n - n)!} = n!\)
Exemple:
Le nombre de manières de placer 8 convives autour d’une table est : \(P_8= 8!\) 40 320 possibilités
3.2. Permutations avec répétitions
Dans le cas où il existerait plusieurs répétitions \(k\) d’un même objet parmi les \(n\) objets, le nombre de permutations possibles des \(n\) objets doit être rapporté aux nombres de permutations des \(k\) objets identiques.
Le nombre de permutations de \(n\) objets est alors : \({P_n} = \frac{n!}{k!}\)
En effet, les permutations de \(k\) objets identiques sont toutes identiques et ne comptent que pour une seule permutation.
Exemple:
Considérons le mot « CELLULE ». Le nombre de mots possibles (avec ou sans signification) que l’on peut écrire en permutant ces 7 lettres est : \({P_7} = \frac{{7!}}{{2!3!}}\) = 420 mots possibles
en considérant deux groupes de lettres identiques : L (3 fois) et E (2 fois).
4. Combinaisons
4.1. Définition
Si l’on reprend l’exemple de la séquence d’ADN, à la différence des arrangements où les dinucléotides AC et CA formaient deux arrangements distincts, ces derniers ne formeront qu’une seule combinaison. Pour les combinaisons, on ne parle plus de suite ni de série puisque la notion d’ordre des objets n’est plus prise en compte. On parle alors de tirages avec ou sans remise.
4.2. Combinaisons sans remise
Étant donné un ensemble \(E\) de \(n\) objets, on appelle combinaisons de \(p\) objets tout ensemble de \(p\) objets pris parmi les \(n\) objets sans remise.
Le nombre de combinaisons de \(p\) objets pris parmi \(n\) est noté : \(C_n^p\)
Remarque : On a nécessairement \(1 \geq p \geq n\) et \(n,p \in N^*\) Si \(n < p\), alors \(C_n^p = 0\)
Exemples : (1) Le tirage au hasard de 5 cartes dans un jeu de 32 (main de poker) est une combinaison avec \(p=5\) et \(n=32\). (2) La formation d’une délégation de 5 personnes parmi un groupe de 50 constitue une combinaison avec \(p=5\) et \(n=50\).
Pour ces deux exemples, les objets tirés sont clairement distincts.
Le nombre de combinaisons de \(p\) objets pris parmi \(n\) et sans remise est : \(C_n^p = \frac{n!}{p!(n - p)!}\) notée \(\binom{n}{p}\) avec \(1 \geq p \geq n\)
Voici pourquoi :
Pour calculer ce nombre, on utilise le principe de la division.
• Il y a \(A_n^p\) manières de tirer \(p\) objets parmi \(n\) en les ordonnant soit \(A_n^p = \frac{n!}{(n - p)!}\)
• Une fois les \(p\) objets tirés, il y a \(p!\) manières de les ordonner.
• Il y a donc \(\frac{A_n^p}{p!}\) manières de tirer \(p\) objets parmi \(n\) sans les ordonner.
\(C_n^p = \frac{A_n^p}{p!} = \frac{1}{p!}\frac{n!}{(n - p)!}\)
Remarque : A la notation ancienne \(C_n^p\), on préfère parfois la notation moderne \(\binom{n}{p}\) . Les nombres \(n\) et \(p\) constituent les coefficients binomiaux.
Exemples:
Dans le cadre de l’exemple de la séquence d’ADN, le nombre de dinucléotides attendus sans tenir compte de l’ordre des bases dans la séquence (hypothèse justifiée dans le cas de l’ADN non codant) est donc : \(C_4^2 = \binom{4}{2} = \frac{4!}{2!(4-2)!} = \frac{4 \times 3 }{2 \times 1} =\) 6 dinucléotides
Les 6 dinucléotides possibles sous cette hypothèse sont :

Ceci correspond aux 12 arrangements possibles sans répétitions (\(A_n^p = \frac{n!}{(n - p)!}\)) divisé par le nombre de permutations possibles avec 2 nucléotides (\({P_p} = p!\)).
4.3. Combinaisons avec remise
Le nombre de combinaisons de \(p\) objet parmi \(n\) avec remise est : \(C_{n + p - 1}^p = \frac{(n + p - 1)!}{p!(n - 1)!}\)
Voici pourquoi :
Soit la constitution de mots de 3 lettres à partir d’un alphabet à 5 lettres avec remise, on distingue 3 cas possibles :
• \(C_5^3\) nombre de mots de 3 lettres différentes et sans ordre
• \(C_5^2 \times 2\) nombre de mots de 2 lettres différentes et une lettre redondante
• \(C_5^1\) nombre de mots de 3 lettres identiques
d’où au total : \(C_5^3\) + 2 \(C_5^2\)+ \(C_5^1\) = \(C_7^3 = 35\) en utilisant la formule des combinaisons composées ou formule de Pascal.
en effet \(C_5^3 + C_5^2 = C_6^3\) et \(C_5^2 + C_5^1 = C_6^2\) d’où \(C_5^2 + C_5^1 = C_6^2\) soit $ C_7^3 = 35$ mots possibles de 3 lettres à partir d’un alphabet à 5 lettres.
ainsi \(C_7^3 = C_{5+3-1}^3 = C_{n+p-1}^p\) avec n=5 et p=3
4.4. Propriétés des combinaisons
4.4.1. La symétrie
Le nombre de combinaisons de \(p\) objets pris parmi \(n\) étant \(C_p^n = \frac{n!}{p!(n − p)!}\), alors
\(C_n^0 = C_n^n = 1\) car \(C_n^0 = C_n^n = \frac{n!}{n!}\)
si \(n \geq 1 \qquad C_n^1 = C_n^{n-1} = n\) car \(C_n^1 = C_n^{n-1} = \frac{n!}{(n-1)!}\)
si \(n \geq 2 \qquad C_n^2 = C_n^{n-2} = = \frac{n(n-1)}{2}\)
avec \(C_n^2 = C_n^{n-2} = \frac{n!}{2!n-2!} = \frac{n \times (n-1)(n-2) !}{2!n-2!}\)
Par récurrence, on déduit des relations précédentes, la propriété de symétrie à savoir :
si \(0 \leq p \leq n \qquad C_p^{n-p} = \frac{n!}{p!(n − p)!}\) ainsi \(C_n^p = C_n^{n-p}\)
Il revient au même de donner la combinaison des \(p\) objets choisis ou bien celle des \((n-p)\) qui ne le sont pas.
4.4.2 Combinaisons composées ou Formule de Pascal
si \(0 \leq p \leq n-1 \qquad\) \(C_{n-1}^{p-1} + C_{n-1}^p = C_n^p\)
Voici pourquoi : Parmi les \(n\) objets, on considère un objet en particulier. - Si cet objet fait partie des \(p\) objets tirés, il y a \(C_{n−1}^{p-1}\) possibilités de choisir les \(p-1\) autres objets parmi les \(n-1\) objets restants. - Si en revanche, l’objet ne fait pas partie du tirage, il y a \(C_{n-1}^p\) possibilités de choisir les \(p\) autres objets parmi les \(n-1\) objets restants.
d’où la relation \(C_{n−1}^{p−1} + C_{n−1}^p = C_n^p\)
Les termes du triangle de Pascal résultent de l’application directe de cette relation.
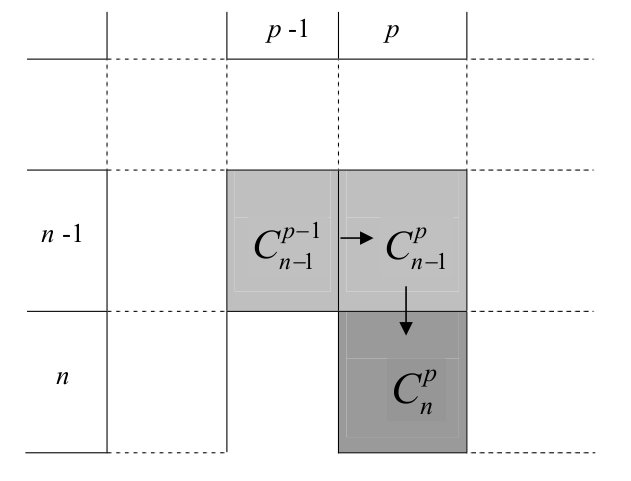
Pour établir le triangle de Pascal, il suffit de porter les valeurs prises par \(p\) en colonne et celles prises par \(n\) en ligne (voir tableau ci-dessus). La valeur attribuée à chaque case, \(C_n^p\), est obtenue en faisant la somme de la valeur de la case située juste au-dessus, \(C_{n - 1}^p\) et la valeur de la case située au-dessus et à gauche \(C_{n - 1}^{p - 1}\). Ceci correspond à l’application de la propriété énoncée précédemment.
Le triangle de Pascal permet d’obtenir par récurrence les coefficients numériques ou coefficient binomiaux du binôme de Newton.
4.4.3 Formule du binôme de Newton
La formule du binôme de Newton correspond à la décomposition des différents termes de la puissance \(n^ième\) du binôme \((a+b)\).
\(\forall(a,b) \in \mathbb{R} , n \in \mathbb{N}, (a+b)^n = \sum\limits_{p = 0}^ n C_{n}^p a^{n - p} b^p = \sum\limits_{p = 0}^n \binom{n}{p} a^{n - p} b^p\)
Elever \((a+b)\) à la puissance \(n\) revient à multiplier \(n\) binômes identiques \((a+b)\). Le résultat est une somme où chaque élément est le produit de \(n\) facteurs de type \(a\) ou \(b\) choisi chacun dans un binôme différent. Les termes sont ainsi de la forme \(a^{n - p} b^p\). Chacun de ces termes est obtenu autant de fois qu’il existe de façons de choisir les \(p\) éléments \(a\) parmi les \(n\), c’est à dire le nombre de combinaisons \(C_n^p\).
Compte tenu de la symétrie des combinaisons \(C_n^p\), la formule du binôme de Newton peut s’écrire :
\({(a + b)^n} = \sum\limits_{p = 0}^n {C_n^p} {a^{n - p}} {b^p} = \sum\limits_{q = 0}^n {C_n^q} {a^q}{b^{n - q}} \qquad \text{avec} \qquad q = n – p\)
Les coefficients binomiaux, \(C_n^p\) ou \(\binom{n}{p}\) qui sont les coefficients de la formule du binôme de Newton figurent dans de nombreuses formules mathématiques, notamment pour le calcul des probabilités de la loi binomiale. Ces coefficients peuvent être obtenus facilement à l’aide du triangle de Pascal.
Exemple:
Le développement de \((a+b)^6\) donne :
\((a + b)^6 = \sum\limits_{p = 0}^6 \binom{6}{p}a^{6-p}b^p\)
\((a + b)^6 = \binom{6}{0}a^6 + \binom{6}{1}a^5 b + \binom{6}{2}a^4 b^2 + \binom{6}{3}a^3 b^3 + \binom{6}{4}a^2 b^4 + \binom{6}{5}a b^5 + \binom{6}{6} b^6\)
L’application du triangle de Pascal(7e ligne) donne directement les valeurs des coefficients binomiaux :
\((a + b)^6 = {a^6} + 6{a^5}b + 15{a^4}{b^2}4 + 20{a^3}{b^3} + 15{a^2}{b^4} + 6a{b^5} + {b^6}\)
Remarque : Si l’on pose \(a = b = 1\), on obtient alors, d’après la formule du binôme de Newton,
\({(2)^n} = \sum\limits_{p = 0}^n {C_n^p}\)
Or \(C_n^p\) étant le nombre de parties à \(p\) éléments de l’ensemble \(E\) contenant \(n\) objets, \(\sum\limits_{p = 0}^n {C_n^p}\) représente le nombre de parties ou partitions de l’ensemble \(E\) que l’on note \(\mathcal{P}(\Omega)\)
Si \(\text{card}\ E = n\) alors \(\text{card}\ \mathcal{P}(E)= {2^n}\) (Voir Systeme complet d’évènements)
Le cardinal d’un ensemble (\(\text{card}\)) correspond au nombre d’éléments constituant cet ensemble.