Chapitre 2/ Limites – Continuité
Sandrine CHARLES
Introduction
L’objet du second chapitre d’analyse est de présenter les notions de limites et de continuité des fonctions réelles d’une variable réelle définies dans le chapitre 1. Ce chapitre comprend deux parties sub-divisées comme indiqué sur la gauche de votre écran.
L’introduction officielle de la notion de limite dans le langage mathématique remonte à 1751, date à laquelle paraît l’Encyclopédie de Diderot et d’Alembert.
Comme cela est largement détaillé sur le site http://chronomath.irem.univ-mrs.fr/chronom2/limiteDD.html, Cauchy publia en 1821 un Cours d’analyse, réédité aujourd’hui dans un but pédagogique et épistémologique (collection ellipses, Ed. Marketing). Ce cours eut une très grande audience et constitue le premier exposé rigoureux sur les fonctions numériques. Rénovant l’analyse fonctionnelle, Cauchy formalise, en particulier, la notion de limite et celle de continuité sur un intervalle :
Si les valeurs successivement attribuées à une variable s’approchent indéfiniment d’une valeur fixe, de manière à finir par en différer aussi peu que l’on voudra, alors cette dernière est appelée la limite de toutes les autres.
\(h\) désignant une quantité infiniment petite, lorsque, la fonction \(f(x)\) admettant une valeur unique et finie pour toutes les valeurs de \(x\) comprises entre deux limites données, la différence \(f(x + h) - f(x)\) est toujours entre ces limites une quantité infiniment petite, on dit que \(f(x)\) est une fonction continue de la variable \(x\) entre les limites dont il s’agit.
Intuitivement et graphiquement, on décrit la courbe représentative de \(f\) sans lever le crayon : pas de “trous”. Ci-contre à gauche, on a un arc de courbe continu, à droite, il y a discontinuité au point \(x = a\).

Vous trouverez sur les sites suivants quelques exemples de « culture générale » ou de la vie courante où apparaît la notion de limite :
Exercices corrigés
Ci-dessous, deux sites intéressants permettant de s’exercer sur d’autres exemples que ceux de votre polycopié de travaux dirigés :
1 Limites
1.1 Définitions
1.1.1 Limite en un point
Définitions :
Soient \(f:I \to \mathbb{R}\) et \({x_0} \in I\) (\({x_0}\) peut être une des extrémités de \(I\)).
· Soit \(\ell \in \mathbb{R}\). On dit que $$ est limite de \(f\) en \({x_0}\), ou bien que \(f\left( x \right)\) tend vers $$ lorsque \(x\) tend vers \({x_0}\) (\(x \to {x_0}\)), si : * \(\forall \varepsilon > 0,{\text{ }}\exists \alpha > 0\) tel que \(x \in I\) et $| {x - {x_0}} | < | {f( x ) - } | $
On note ${x } f( x ) = $ ou ${{x_0}} f( x ) = $ ou $f( x )$
· On dit que \(+ \infty\) est limite de* f* en \({x_0}\) ($_{x } f( x ) = + $) si : * \(\forall A \in \mathbb{R},{\text{ }}\exists \alpha > 0\) tel que \(x \in I\) et \(\left| {x - {x_0}} \right| < \alpha \Rightarrow f\left( x \right) \geqslant A\)
· De même, on dit que \(- \infty\) est limite de \(f\) en \({x_0}\) ($_{x } f( x ) = - $) si : * \(\forall A \in \mathbb{R},{\text{ }}\exists \alpha > 0\) tel que \(x \in I\) et \(\left| {x - {x_0}} \right| < \alpha \Rightarrow f\left( x \right) \leqslant A\)
1.1.2 Limites en \(+ \infty\) et \(- \infty\)
Définition
Soit \(f:I \to \mathbb{R}\). On suppose que \(I = \left[ {a; + \infty } \right[\).
· Soit \(\ell \in \mathbb{R}\). On dit que $$ est limite de \(f\) en \(+ \infty\) si : * \(\forall \varepsilon > 0,{\text{ }}\exists B \in \mathbb{R}\) tel que $x B | {f( x ) * } | $
On note ${x + } f( x ) = $ ou ${ + } f( x ) = $ ou $f( x )$
On dit que \(+ \infty\) est limite de \(f\) en \(+ \infty\) si : * \(\forall A \in \mathbb{R},{\text{ }}\exists B \in \mathbb{R}\) tel que \(x \geqslant B \Rightarrow f\left( x \right) \geqslant A\)
On dit que \(- \infty\) est limite de \(f\) en \(+ \infty\) si : * \(\forall A \in \mathbb{R},{\text{ }}\exists B \in \mathbb{R}\) tel que \(x \geqslant B \Rightarrow f\left( x \right) \leqslant A\)
Définition (*limite en Erreur ! Des objets ne peuvent pas être créés à partir des codes de champs de mise en forme.) :
Soit \(f:I \to \mathbb{R}\). On suppose que \(I = \left] { - \infty ;a} \right]\).
- Soit \(\ell \in \mathbb{R}\). On dit que $$ est limite de \(f\) en \(- \infty\) si : * \(\forall \varepsilon > 0,{\text{ }}\exists B \in \mathbb{R}\) tel que $x B | {f( x ) * } | $
On note ${x - } f( x ) = $ ou ${ - } f( x ) = $ ou $f( x )$
On dit que \(+ \infty\) est limite de* f* en \(- \infty\) si : * \(\forall A \in \mathbb{R},{\text{ }}\exists B \in \mathbb{R}\) tel que \(x \leqslant B \Rightarrow f\left( x \right) \geqslant A\)
On dit que \(- \infty\) est limite de* f* en \(- \infty\) si : * \(\forall A \in \mathbb{R},{\text{ }}\exists B \in \mathbb{R}\) tel que \(x \leqslant B \Rightarrow f\left( x \right) \leqslant A\)
Proposition
Si \(\ell \in \mathbb{R}\), alors \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \ell \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} \left( {f\left( x \right) - \ell } \right) = 0\)
Si \({x_0} \in \mathbb{R}\), alors ${x } f( x ) = {h 0} f( {{x_0} + h} ) = $
1.1.3 Limite par valeurs supérieures ou inférieures
Définition :
Soit \(f:I \to \mathbb{R}\) telle que $_{x } f( x ) = $ (\({x_0} \in \bar{\mathbb{R}}\)).}Quand \(x\) tend vers \({x_0}\), on dit que \(f\left( x \right)\) tend vers $$ par valeurs supérieures (resp. inférieures) si, au voisinage de \({x_0}\), $f( x ) $ (resp. $f( x ) $).
On note alors \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = {\ell ^ + }\) (resp. \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = {\ell ^ - }\)).
Exemple
Considérons la fonction définie par \(f\left( x \right) = \frac{{2x + 1}}{{{x^2}}}\). On a \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {0^ + }\) et \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {0^ - }\).
1.1.4 Limites à gauche et à droite
Définition (limite à gauche)* :
Soit \(\ell \in \mathbb{R}\). Alors
\(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = \ell \Leftrightarrow \forall \varepsilon > 0,{\text{ }}\exists B > 0\) tel que $( {{x_0} - B x < {x_0}} ) | {f( x ) - } | $.
\(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \Leftrightarrow \forall A \in \mathbb{R}{\text{, }}\exists * > 0\) tel que \(\left( {{x_0} - B \leqslant x < {x_0}} \right) \Rightarrow f\left( x \right) \geqslant A\).
\(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \Leftrightarrow \forall A \in \mathbb{R}{\text{, }}\exists * > 0\) tel que \(\left( {{x_0} - B \leqslant x < {x_0}} \right) \Rightarrow f\left( x \right) \leqslant A\).
Définition (limite à droite)* :
Soit \(\ell \in \mathbb{R}\). Alors
\(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \ell \Leftrightarrow \forall \varepsilon > 0,{\text{ }}\exists B > 0\) tel que $( {{x_0} < x + B} ) | {f( x ) - } | $.
\(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \Leftrightarrow \forall A \in \mathbb{R}{\text{, }}\exists * > 0\) tel que \(\left( {{x_0} < * \leqslant {x_0} + B} \right) \Rightarrow f\left( x \right) \geqslant A\).
\(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \Leftrightarrow \forall A \in \mathbb{R}{\text{, }}\exists * > 0\) tel que \(\left( {{x_0} < * \leqslant {x_0} + B} \right) \Rightarrow f\left( x \right) \leqslant A\).
1.2 Limites par opération
1.2.1 Limite d’une somme
| limites | ||||||
|---|---|---|---|---|---|---|
| $_{x } f( x ) = $ | $$ | $$ | $$ | $+ $ | \(- \infty\) | $+ $ |
| $_{x } g( x ) = $ | \(\ell '\) | $+ $ | $- $ | $+ $ | $- $ | $- $ |
| $_{x } ( {f + g} )( x ) = $ | \(\ell + \ell '\) | $+ $ | $- $ | $+ $ | $- $ | ? |
?: on parle alors de forme indéterminée
1.2.2 Limite d’un produit
| limites | ||||
|---|---|---|---|---|
| $_{x } f( x ) = $ | $$ | \(\ell \ne 0\) | \(0\) | $+ $ ou \(- \infty\) |
| $_{x } g( x ) = $ | \(\ell '\) | $+ $ ou \(- \infty\) | $+ $ ou \(- \infty\) | $+ $ ou \(- \infty\) |
| $_{x } ( {fg} )( x ) = $ | \(\ell \ell '\) | $+ $ ou \(- \infty\) | ? | $+ $ ou \(- \infty\) |
ou : on décide de $$ suivant le signe de $$, en appliquant la règle des signes.
1.2.3 Limite d’un quotient
| limites | ||||||
|---|---|---|---|---|---|---|
| $_{x } f( x ) = $ | $$ | \(\ell \ne 0\) | $$ | \(+\infty\) ou \(-\infty\) | \(0\) | \(+\infty\) ou \(-\infty\) |
| $_{x } g( x ) = $ | \(\ell ' \ne 0\) | \(0\) | \(+\infty\) ou \(-\infty\) | \(\ell '\) | \(0\) | \(+\infty\) ou \(-\infty\) |
| $_{x } ( {f/g} )( x ) = $ | \(\ell / \ell '\) | $+$ ou \(- \infty\) | \(0\) | $+ $ ou \(- \infty\) | ? | ? |
ou : on décide de \(\pm \infty\) suivant le signe de \(\ell\), en appliquant la règle des signes.
ou : on décide de \(\pm \infty\) suivant le signe de \(\ell '\), en appliquant la règle des signes.
Remarques
Lorsque le numérateur tend vers zéro et le dénominateur vers l’infini, le quotient tend vers zéro : \({0^ * }\) ou \({0^ - }\) selon la règle des signes.
Lorsque le numérateur tend vers l’infini et le dénominateur vers zéro, le quotient tend vers l’infini : \(+ \infty\) ou \(- \infty\) selon la règle des signes.
1.3 Limites par comparaison
Soit \(f:I \to \mathbb{R}\).
Proposition 1
S’il existe une fonction \(g\) et un réel \(A\) tels que \(\forall x \geqslant A{\text{, }}f\left( x \right) \geqslant g\left( x \right)\) et ${x + } g( x ) = + $, alors : ${x + } f( x ) = + $.
Proposition 2
S’il existe une fonction \(g\) et un réel \(A\) tels que \(\forall x \geqslant A{\text{, }}f\left( x \right) \leqslant g\left( x \right)\) et ${x + } g( x ) = - $, alors : ${x + } f( x ) = - $.
Théorème « des gendarmes »
S’il existe deux fonctions \(g\) et \(h\), un réel \(A\) tels que \(\forall x \geqslant A{\text{, }}g\left( x \right) \leqslant f\left( x \right) \leqslant h\left( x \right)\) et ${x + } g( x ) = $ et ${x + } h( x ) = $, alors $_{x + } f( x ) = $.
Proposition 3
S’il existe une fonction \(g\) et un réel \(A\) tels que \(\forall x \geqslant A{\text{, }}\left| {f\left( x \right) - \ell } \right| \leqslant g\left( x \right)\) et \(\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 0\), alors : $_{x + } f( x ) = $.
Proposition 4
S’il existe deux fonctions \(f\) et \(g\) et un réel \(A\) tels que \(\forall x \geqslant A{\text{, }}g\left( x \right) \leqslant f\left( x \right)\) ; si $_{x + } f( x ) = $ et \(\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = \ell '\), alors $’ $.
1.4 Limite d’une fonction composée
Théorème :
Soient \({x_0}\), $$ et \(\ell '\) des nombres réels (« éventuellement » égaux à $ $).
Soient \(f\) et \(g\) deux fonctions dont la composée \(g \circ f\) existe.
Si $_{x } f( x ) = $ et si \(\mathop {\lim }\limits_{x \to \ell } g\left( x \right) = \ell '\), alors \(\mathop {\lim }\limits_{x \to {x_0}} \left( {g \circ f} \right)\left( x \right) = \ell '\).
1.5 Limite à l’infini d’une fonction polynôme ou d’une fraction rationnelle
Méthode
Pour déterminer une limite à l’infini d’une fonction polynôme ou rationnelle, dans le cas où les théorèmes précédents ne s’appliquent pas, on transforme l’expression \(f\left( * \right)\) en factorisant chaque polynôme par le terme de plus haut degré.
Cas d’une fonction polynôme
On cherche à calculer \(\mathop {\lim }\limits_{x \to + \infty } \left( { - {x^2} + ax + b} \right)\) avec \(a,b > 0\).
On a ${x + } - {x^2} = - $ et ${x + } ( {ax + b} ) = + $ ; la somme est indéterminée.
On transforme le polynôme : $ - {x^2} + ax + b = {x^2}( { - 1 + * } )$.
Or \(\mathop {\lim }\limits_{x \to + \infty } \frac{a}{x} = 0\) et \(\mathop {\lim }\limits_{x \to + \infty } \frac{b}{{{x^2}}} = 0\) ;
Donc comme somme \(\mathop {\lim }\limits_{x \to + \infty } \left( { - 1 + \frac{a}{x} + \frac{b}{{{x^2}}}} \right) = - 1\) et comme produit $_{x + } {x^2}( { - 1 + + } ) = - $.
La limite à l’infini d’un polynôme est la limite de son terme de plus haut degré
${x + } ( { - {x^2} + ax + b} ) = {x + } - {x^2} = - $
Cas d’une fraction rationnelle
On cherche à calculer \(\mathop {\lim }\limits_{x \to - \infty } \frac{{a - bx}}{{{x^2} + c}}\) avec \(a,b,c > 0\).
${x - } a - bx = + $ et ${x - } {x^2} + c * + $ ; le quotient est donc indéterminé.
Pour \(x \ne 0\), on * : \(\frac{{a - bx}}{{{x^2} + c}} = \frac{{x\left( {\frac{a}{x} - b} \right)}}{{{x^2}\left( {1 + \frac{c}{{{x^2}}}} \right)}} = \frac{1}{x}\frac{{\left( {\frac{a}{x} - b} \right)}}{{\left( {1 + \frac{c}{{{x^2}}}} \right)}}\). Ainsi :
\(\mathop {\lim }\limits_{x \to - \infty } \frac{a}{x} = 0\) et \(\mathop {\lim }\limits_{x \to - \infty } \frac{c}{{{x^2}}} = 0\), donc : \(\mathop {\lim }\limits_{x \to - \infty } \frac{a}{x} - b = - b\) et \(\mathop {\lim }\limits_{x \to - \infty } 1 + \frac{c}{{{x^2}}} = 1\). Finalement :
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{\frac{a}{x} - b}}{{1 + \frac{c}{{{x^2}}}}} = - b\) et donc \(\mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}\frac{{\frac{a}{x} - b}}{{1 + \frac{c}{{{x^2}}}}} = {0^ - }\)
La limite à l’infini d’une fraction rationnelle est égale à la limite du quotient simplifié de ses termes de plus haut degré
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{a - bx}}{{{x^2} + c}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - bx}}{{{x^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - b}}{x} = 0\)
1.6 Limites et courbe représentative d’une fonction
1.6.1 Etude des branches infinies
Considérons une fonction \(f\) définie sur un domaine \({D_f}\) de \(\mathbb{R}\). Soit $$ sa courbe représentative.
Proposition 1
Si $_{x } f( x ) = $, alors la droite \(x = {x_0}\) est asymptote à la courbe $$.
1.6.2 Direction asymptotique
On recherche une direction asymptotique lorsque $_{x } f( * ) = $.
 * * * *
* * * *
D’après AZOULAY et AVIGNANT
La courbe $$* admet* une direction asymptotique si la droite OM tend vers une position limite lorsque le point \(M\) s’éloigne à l’infini sur $$.
Le coefficient directeur de OM est \(\frac{{f\left( x \right)}}{x}\). S’il existe une direction asymptotique, alors \(\frac{{f\left( * \right)}}{x}\) tend vers une limite finie $$.
Si $ $ lorsque $x $, on dit que $$ admet une branche parabolique dans la direction Oy.
1.6.3 Asymptotes
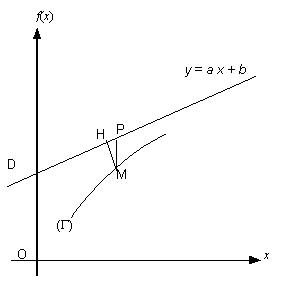
D’après AZOULAY et AVIGNANT
La courbe $$ admet une asymptote oblique \(D\) d’équation \(y = ax + b\), si la distance entre \(M\) et la droite \(D\) ($ $) tend vers 0 lorsque \(M\) s’éloigne à l’infini sur $$.
La pente de \(D\) est :
\(a = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{f\left( x \right)}}{x}\)
Pour déterminer l’ordonnée à l’origine de \(D\), on montre que \(f\left( x \right) - ax\) tend vers \(b\) lorsque $x $, ou bien alors que \(f\left( x \right) - ax - b\) tend vers 0 lorsque $x $.
Si \(f\left( x \right) - ax \to \pm \infty\), on dit que \(\Gamma\) admet une branche parabolique de pente \(a\).
2 Continuité
2.1 Continuité en un point - Continuité sur un intervalle
Définitions
Soit \(f\) une fonction définie sur \(I \subseteq \mathbb{R}\). Soit \({x_0} \in I\).
On dit que \(f\) est continue en \({x_0}\) si et seulement si \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\), c’est-à-dire si : * \(\forall \varepsilon > 0,{\text{ }}\exists \alpha > 0\) tel que \(x \in I\) et $| {x - {x_0}} | < | {f( x ) - f( {{x_0}} )} | $
\(f\) est continue à droite (resp. à gauche) si on rajoute la condition \(x \geqslant {x_0}\) (resp. \(x \leqslant {x_0}\)).
Conséquences
\(f\) est continue en \({x_0}\) si et seulement si \(f\) est continue à droite et à gauche en \({x_0}\).
\(f\) est continue sur I si et seulement si \(f\) est continue en tout point de \(I\).
2.1.1 Opérations sur les fonctions continues
Propositions
Soient \(f\) et \(g\) deux fonctions définies sur \(I \subseteq \mathbb{R}\) et continues en \({x_0}\) (resp. sur \(I\)).
\(\forall \alpha ,\beta \in \mathbb{R}\), \(\alpha f + \beta g\) est continue en \({x_0}\) (resp. sur \(I\)).
Si \(g\left( {{x_0}} \right) \ne 0\), alors \(\frac{1}{g}\) est continue en \({x_0}\) (resp. sur \(I\)).
Si \(g\left( {{x_0}} \right) \ne 0\), alors \(\frac{f}{g}\) est continue en \({x_0}\) (resp. sur \(I\)).
Exemples
Toute fonction constante est continue sur \(\mathbb{R}\).
Les fonctions polynomiales sont continues sur \(\mathbb{R}\). Autres
Remarques
Pour démontrer qu’une fonction est continue, il suffit souvent de vérifier qu’il s’agit d’un « mélange » de fonctions continues classiques, et les propositions précédentes ainsi que la suivante s’appliquent.
Proposition 2
Soient \(f\) et \(g\) deux fonctions définies sur \(I \subseteq \mathbb{R}\). Si \(f\) est continue en \({x_0}\) (resp. sur \(I\)) et \(g\) continue en \(f\left( {{x_0}} \right)\), alors \(g \circ f\) est continue en \({x_0}\) (resp. sur \(I\)).
La démonstration de cette proposition découle directement de celle du théorème 1.4.
2.1.2 Prolongement par continuité
Si \(f\) est une fonction définie sur \(I\backslash \left\{ {{x_0}} \right\}\) et si \(\mathop {\lim }\limits_{x \to {x_0}} f\left( * \right) = a\), on dit que \(g\) est un prolongement par continuité de \(f\) en \({x_0}\) si et seulement si \(g\left( x \right) = f\left( x \right)\) \(\forall x \ne {x_0}\) et \(g\left( {{x_0}} \right) = a\).
2.2 Propriétés des fonctions continues
2.2.1 Théorème des valeurs intermédiaires
Théorème
Soit \(f\) continue sur \(I\). Soient \(a\) et \(b\) deux éléments de \(I\) tels que \(a < b\). Alors, en supposant que \(f\left( a \right) < f\left( b \right)\), pour tout \(y\) tel que \(f\left( a \right) \leqslant y \leqslant f\left( b \right)\), il existe au moins un élément \(x \in \left] {a,b} \right[\) tel que \(y = f\left( x \right)\).
Corollaire 1
Soit \(f\) continue sur \(\left[ {a,b} \right]\). Si \(f\left( a \right)f\left( b \right) \leqslant 0\), alors \(\exists c \in \left] {a,b} \right[\) tel que \(f\left( c \right) = 0\).
Exercice
Une personne parcourt à vélo une distance de 20 km en une heure. Montrer qu’il existe un intervalle de temps d’une demi-heure pendant lequel elle parcourt exactement 10 km.
Corollaire 2
L’image d’un intervalle par une fonction continue est un intervalle.
!* Attention* :
Si \(I\) a pour bornes \(a\) et \(b\), celles de \(f\left( I \right)\) ne sont pas nécessairement \(f\left( a \right)\) et \(f\left( b \right)\).
2.2.2 Théorème de la bijection réciproque
Théorème
Si \(f:I \to J\) est continue et strictement monotone sur \(I\), alors \(f\) réalise une bijection de \(I\) sur \(J\). De plus, la fonction réciproque \({f^{ - 1}}\), de \(J\) vers \(I\), est continue et strictement monotone (avec la même monotonie que \(f\)).
Remarques
Les courbes représentatives de \(f\) et \({f^{ - 1}}\) sont symétriques l’une de l’autre dans la symétrie par rapport à la droite \(y = x\) parallèlement à la droite \(y = - x\) ; si le repère est orthonormé, il s’agit de la symétrie orthogonale par rapport à la droite \(y = x\). Exemple.
Le théorème des valeurs intermédiaires montre l’existence d’une solution à l’équation \(f\left( x \right) = 0\). Le théorème de la bijection réciproque en assure l’unicité.
3 Pour aller plus loin
Qu’est-ce qu’un nombre réel ? Théorème de Bolzano-Weierstrass
Notion d’équivalents (§ 7.3)
Continuité uniforme (§ 7.4.5)
Fonctions \(k\)-lipschitziennes (§ 7.4.6)
4 Exemple d’application en Biologie
L’exemple présenté ci-après est extrait de LEFORT G. (1967) p111.
Pour exciter un tissu (nerf ou muscle), un courant électrique doit avoir une intensité au moins égale à une certaine valeur \(i\) qui dépend du temps \(t\) de passage du courant ; on admet la formule approchée :
\(i = {i_0} + \frac{c}{t}\) avec \({i_0}\), \(c\) des constantes positives * *
Considérons la fonction définie par \(f:t \to {i_0} + \frac{c}{t}\) pour tout \(t > 0\).
\(\mathop {\lim }\limits_{t \to + \infty } f\left( t \right) = {i_0}\)
Cette limite à une signification biologique simple : quel que soit le temps de passage du courant, son intensité est toujours supérieure à \({i_0}\) ; ce nombre \({i_0}\) est appelé la rhéobase.
$_{t } f( t ) = + $
On définit par ailleurs la chronotaxie, comme le temps $$ de passage nécessaire pour qu’un courant électrique d’intensité \(2{i_0}\) excite le tissu : \(\theta = {c/{i_0}}\)

5 Quelques trucs…
Les opérations sur les limites ne permettent pas toujours de déterminer la limite d’une fonction. Il faut alors changer de chemin et modifier l’écriture de cette fonction… afin de pouvoir les appliquer !
Nous avons vu comment il est possible de connaître la limite à l’infini d’un polynôme ou d’une fonction rationnelle. Voyons maintenant le cas particulier d’une fonction contenant une racine carrée ou une valeur absolue.
5.1 La quantité conjuguée
Soit \(f\) une fonction définie sur \({\mathbb{R}^ + }\) par $f( x ) = - x $.
\(f\left( 0 \right) = 0\). On cherche à déterminer \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
$_{x + } = + $
$_{x + } x = + $
Donc \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\) est de la forme indéterminée « $- $ ».
L’astuce consiste ici à multiplier par la quantité conjuguée
\(f\left( x \right) = \sqrt {x + 4} - \sqrt x = \frac{{\left( {\sqrt {x + 4} - \sqrt x } \right)\left( {\sqrt {x + 4} + \sqrt x } \right)}}{{\sqrt {x + 4} + \sqrt x }}\)
Le numérateur est alors du type \(\left( {a - b} \right)\left( {a + b} \right) = {a^2} - {b^2}\), d’où :
\(f\left( x \right) = \frac{{\left( {x + 4} \right) - x}}{{\sqrt {x + 4} + \sqrt x }} = \frac{4}{{\sqrt {x + 4} + \sqrt x }}\)
$_{x + } + x = + $, donc \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\) Graphe
5.2 Les valeurs absolues
Soit \(f\) une fonction définie sur \(\mathbb{R}\backslash \left\{ { - 1,1} \right\}\) par \(f\left( x \right) = \frac{{1 - 2\left| x \right|}}{{1 - \left| x \right|}}\).
On cherche à déterminer les limites de \(f\left( x \right)\) aux bornes de son domaine de définition.
L’astuce consiste ici à écrire différemment la valeur absolue de \(x\) selon que \(x\) est négatif ou positif
\(\left| x \right| = - x\) si \(x < 0\)
\(\left| x \right| = x\) si \(x > 0\)
Les limites à déterminer sont les suivantes :
\(\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right)\) \(\mathop {\lim }\limits_{x \to - {1^ \pm }} f\left( * \right)\) \(\mathop {\lim }\limits_{x \to {1^ \pm }} f\left( x \right)\)
Commençons par regarder en \(+ \infty\) :
\(x > 0\) donc \(\left| x \right| = x\) et \(f\left( x \right) = \frac{{1 - 2x}}{{1 - x}}\), donc \(\mathop{\lim }\limits_{x \to + \infty * f(x)} = \mathop{\lim }\limits_{x \to + \infty } \frac{{ - 2x}}{{ - x}} = 2\)En \(- \infty\) :
\(x < 0\) donc \(\left| x \right| = - x\) et \(f\left( x \right) = \frac{{1 + 2x}}{{1 + x}}\), donc \(\mathop {\lim }\limits_{x \to - \infty * f\left( x \right)} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x}}{x} = 2\)En \(- {1^ + }\) :
\(x < 0\) donc \(\left| x \right| = - x\) et \(f\left( x \right) = \frac{{1 + 2x}}{{1 + x}}\), donc \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{ - 1}}{{1 + x}} = - \infty \quad \left( {x > - 1} \right)\)En \(- {1^ - }\) :
On a toujours \(x < 0\) donc \(\left| x \right| = - x\) et \(f\left( x \right) = \frac{{1 + 2x}}{{1 + x}}\), mais cette fois-ci
\(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{ - 1}}{{1 + x}} = + \infty \quad \left( {x < - 1} \right)\)En \({1^ + }\) :
\(x > 0\) donc \(\left| x \right| = x\) et \(f\left( x \right) = \frac{{1 - 2x}}{{1 - x}}\), donc \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{ - 1}}{{1 - x}} = + \infty \quad \left( {x > 1} \right)\)En \({1^ - }\) :
\(x > 0\) donc \(\left| x \right| = x\) et \(f\left( x \right) = \frac{{1 - 2x}}{{1 - x}}\), donc \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{ - 1}}{{1 - x}} = - \infty \quad \left( {x > 1} \right)\)