Chapitre 1 - Fonctions – Généralités
Sandrine CHARLES
N’hésitez pas à consulter la liste des symboles en cas de doute sur leur signification
Introduction

Lune
Pour certains, la qualité du sommeil est fonction de la phase de la lune, celle-ci déterminant également la qualité des légumes à venir. Si l’on gratte un peu, on s’aperçoit que pour les uns, la pleine lune serait favorable, alors que ce serait le contraire pour d’autres.
En mathématiques, une fonction est communément donnée par une règle de calcul associant à un nombre (voir plusieurs…) appelé variable, souvent noté \(x\), une image obtenue en appliquant les règles de calcul définissant la fonction.
D’un point de vue historique, c’est Leibniz qui précise le concept de fonction (le terme est de lui, 1692 : en latin functio = accomplissement, exécution).
Ce premier chapitre d’analyse présente les principales définitions nécessaires à l’étude des fonctions réelles d’une variable réelle. Chaque paragraphe va permettre de rappeler pas à pas les notions de base du programme de secondaire.
1 Définitions
1.1 Intervalles – voisinage
\(a\) et \(b\) étant deux réels, l’ensemble \(\left\{ {x \in \mathbb{R}/a < x < b} \right\}\) est l’intervalle ouvert noté \(\left] {a,b} \right[\) ;
\(a\) et \(b\) sont les bornes de l’intervalle.

L’ensemble \(\left\{ {x \in \mathbb{R}/a \leqslant x \leqslant b} \right\}\) est l’intervalle fermé noté \(\left[ {a,b} \right]\), bornes comprises.
Les intervalles \(\left] {a,b} \right]\) (\(a < x \leqslant b\)) et \(\left[ {a,b} \right[\) (\(a \leqslant x < b\)) sont semi-ouverts (ou semi-fermés).
Par extension, on a :
\(x \in \left[ {a, + \infty } \right[ \Leftrightarrow x \geqslant a\) ceci qui s’écrit aussi \(\left[ {a, + \infty } \right[ = \left\{ {x \in \mathbb{R}/x \geqslant a} \right\}\)
\(x \in \left] {a, + \infty } \right[ \Leftrightarrow x > a\)
\(x \in \left] { - \infty ,a} \right] \Leftrightarrow x \leqslant a\)
\(x \in \left] { - \infty ,a} \right[ \Leftrightarrow x < a\)
L’intervalle \(\left] * - \infty , + \infty \right[\) est exactement égal à \(\mathbb{R}\). On note \(\bar{\mathbb{R}}= \mathbb{R} \cup \left\{ { - \infty , + \infty } \right\}\).
Dans ce cours, on appellera voisinage de \(a\), \(a \in \mathbb{R}\), tout intervalle ouvert de \(\mathbb{R}\) contenant \(a\). Ainsi, \(\forall {\alpha _0} > 0\), \(\left] {a - {\alpha _0},a + {\alpha _0}} \right[\) est un voisinage de \(a\).

1.2 Fonctions réelles d’une variable réelle
Une fonction (ou application) réelle d’une variable réelle est une transformation qui à tout élément d’une partie (souvent appelée domaine) \(D \subset \mathbb{R}\) fait correspondre un unique élément de \(\mathbb{R}\). Ainsi :
\(\forall x \in D\), \(\exists !y \in \mathbb{R}\) tel que \(y = f\left( x \right)\)


Par exemple, la température d’une espèce de lézard (\(y\)) en fonction de la température de l’air à l’ombre (\(x\)) est approximativement :
\(y = f\left( x \right) = x\) *
La température (\(y\)) d’une souris dans les mêmes conditions sera approximativement :
\(y = g\left( x \right) = c\) avec \(c\) constante
\(D\) (souvent noté \({D_f}\)) est l’ensemble de définition (ou ensemble de départ) de \(f\). \(D\) est le plus souvent un intervalle ou une réunion d’intervalles.
\(f\left( D \right)\) est l’ensemble d’arrivée de \(f\) ou image de \(D\) par \(f\) :
\(f\left( D \right) \subseteq \mathbb{R}\) et \(f\left( D \right) = \left\{ {f\left( x \right)/x \in D} \right\}\)
Remarque
Les éléments de \(f\left( D \right)\) sont appelés les images.
Les éléments de \(D\) sont appelés les antécédents.
1.3 Graphe d’une fonction
Le graphe d’une fonction \(f\) (ou courbe représentative de \(f\)) dans un repère cartésien \(\left( {Ox,Oy} \right)\), en général orthonormé, est l’ensemble des points de coordonnées \(\left( {x,y = f\left( x \right)} \right)\), avec \(x \in D\) domaine de définition de \(f\) : \[{\text{Graphe}}\left( f \right) = \left\{ {\left( {x,f\left( x \right)} \right)/x \in {D_f}} \right\}\].
Exemple :
2 Opérations sur les fonctions
**Dans toute la suite du cours d’analyse, \(I\) et \(J\) désigneront des intervalles de \(\mathbb{R}\).
Définition 1 :
Soient \(f\) et \(g\) deux fonctions définies sur \(I \subseteq \mathbb{R}\) :
\(f = g \Leftrightarrow \forall x \in I,f\left( x \right) = g\left( x \right)\)
\(\forall x \in I,\left( {f + g} \right)\left( x \right) = f\left( x \right) + g\left( x \right)\)
\(\forall x \in I,\left( {fg} \right)\left( x \right) = f\left( x \right)g\left( x \right)\)
\(\forall x \in I,\left( {\frac{f}{g}} \right)\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) si \(\forall x \in I,g\left( x \right) \ne 0\). *
Définitions 2 :
Soient \(f\) et \(g\) deux fonctions définies sur \(I \subseteq \mathbb{R}\) :
Si \(f\) est inversible (\(\forall x \in I,f\left( x \right) \ne 0\)), \(\forall x \in I,\left( {\frac{1}{f}} \right)\left( x \right) = \frac{1}{{f\left( x \right)}}\).
\(\forall x \in I,\forall \alpha \in \mathbb{R}\quad \left( {\alpha f} \right)\left( x \right) = \alpha f\left( x \right)\).
\(\forall x \in I,\left( { - f} \right)\left( x \right) = - f\left( x \right)\)
Définition 3
Soit \(f\) une fonction définie sur \(I \subseteq \mathbb{R}\). Quand elle existe, la fonction \((1/f)\) est appelée fonction inverse de \(f\) ; la fonction \(\left( - f \right)\) est appelée fonction opposée de \(f\).
3 Fonction composée – Fonction réciproque
3.1 Fonction composée
Définition :
Soient deux fonctions, \(f\) définie sur un intervalle \(I \subseteq \mathbb{R}\) et \(g\) définie sur un intervalle \(J \subseteq \mathbb{R}\) tel que \(\forall x \in I,f\left( x \right) \in J\) (i.e., \(f\left( * \right) \subseteq J\)).
La fonction composée \(g \circ f\) est la fonction définie sur \(I\) par \(\left( {g \circ f} \right)\left( x \right) = g\left( {f\left( x \right)} \right)\) : * \(x\xrightarrow{f}f\left( x \right)\xrightarrow{g}g\left( {f\left( x \right)} \right) = \left( {g \circ f} \right)\left( x \right)\)
où \(x \in I\) et \(f\left( x \right) \in J\), afin que \(g\left( {f\left( x \right)} \right)\) existe.
Remarque
Si \(g \circ f\) existe, la fonction composée \(f \circ g\) n’existe pas toujours, et lorsque \(f \circ g\) existe alors en général \(g \circ f \ne f \circ g\).
Exemples
Soient \(f\) définie par $f( * ) = x $ avec \({D_f} = {\mathbb{R}^ + }\) \(g\) définie par \(g\left( x \right) = \frac{{1 + x}}{{1 - x}}\) avec \({D_g} = \mathbb{R}\backslash \left\{ 1 \right\}\) Que peut-on dire de \(g \circ f\) et \(f \circ g\) ? Réponse
Soient \(f\) définie par \(f\left( * \right) = 2{x^2} + x + 1\) avec \({D_f} * \mathbb{R}\) \(g\) définie par \(g\left( x \right) = \frac{{1 + x}}{{1 - x}}\) avec \({D_g} = \mathbb{R}\backslash \left\{ 1 \right\}\). Que peut-on dire de \(g \circ f\) et \(f \circ g\) ? Réponse
3.2 Injectivité, surjectivité, bijectivité
- On dit qu’une fonction \(f:I \to J\) est injective si tout élément de \(f\left( * \right)\) est l’image d’un seul élément de \(I\). Autrement dit, \(f\) est injective si et seulement si : \(f\left( {{x_1}} \right) = f\left( {{x_2}} \right) \Rightarrow {x_1} = {x_2}\) L’injectivité d’une fonction se traduit également par le fait que « tout élément de \(J\) admet au plus un antécédent par \(f\) dans \(I\) ».
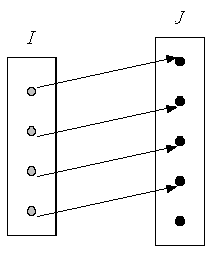
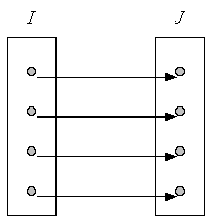
- On dit qu’une fonction \(f:I \to J\) est surjective si \(f\left( * \right) = J\), autrement dit si tout élément de \(J\) est l’image par \(f\) d’au moins un élément de \(I\).

Remarque : La fonction \(f:I \to f\left( I \right)\) est toujours surjective.
- On dit qu’une fonction \(f:I \to J\) est bijective si elle est à la fois injective et surjective.
Exemples
3.3 Fonction réciproque
3.3.1 Définition
Définition
Soit \(f:I \to J\). On dit que f admet une fonction réciproque s’il existe \(g:J \to I\) telle que \(f \circ g = I{d_J}\) et \(g \circ f = I{d_I}\).
On dit alors que \(g\) est la fonction réciproque de \(f\) et on note \(g = {f^{ - 1}}\).
Proposition
Soit \(f:I \to J\). Alors \(f\) admet une fonction réciproque si et seulement si \(f\) est bijective.
Remarques
Par extension, la définition et la proposition précédentes restent valables pour une fonction \(f:{D_1} \to {D_2}\), où \({D_1}\) et \({D_2}\) sont des parties de \(\mathbb{R}\).
Sous l’hypothèse que \({f^{ - 1}}\) existe, si l’image de \(x\) par \(f\) est \(y\), alors l’image de \(y\) par \({f^{ * 1}}\) est \(x\) ; en d’autres termes :
\(y = f\left( x \right) \Leftrightarrow x = {f^{ - 1}}\left( y \right)\)Il ne faut pas confondre la fonction réciproque \({f^{-1}}\), avec la fonction inverse \({1/f}\).
3.3.2 Conséquences
Si \({f^{ - 1}}\) existe, alors \(f \circ {f^{ - 1}} = {f^{ - 1}} \circ f = Id\), où \(Id\) est la fonction identité :
\(f \circ {f^{ - 1}}:J \to J\) donc \(f \circ {f^{ - 1}} = I{d_J}\) avec \(I{d_J}:J \to J,y \mapsto y\)
\({f^{ - 1}} \circ f:I \to I\) donc \({f^{ * 1}} \circ f = I{d_I}\) avec \(I{d_I}:I \to I,x \mapsto x\)
Du point de vue graphique, les représentations de deux fonctions réciproques se déduisent l’un de l’autre par une symétrie par rapport à la première bissectrice.
Exemples :
- Soit la fonction \(f\) définie par \(f\left( * \right) = ax + b\) avec \(a \ne 0\).
On a donc \(y = ax + b\) d’où l’on tire \(x = \frac{{y - b}}{a}\).
Donc la fonction réciproque de \(f\) est définie par \(g\left( * \right) = \frac{{x - b}}{a}\). Vérification
- Soit la fonction \(f\) définie par \(f(x) * \frac{{x - 1}}{{x + 2}}\).
La fonction réciproque \(g\) est alors définie par \(g\left( * \right) = \frac{{1 + 2x}}{{1 - x}}\). Vérification
3.3.3 Application : définition de la fonction racine carrée
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par :
\(y = f\left( x \right) = {x^2}\)
Nous avons vu plus haut que la fonction \(f\) n’est pas bijective puisqu’à une valeur de \(y\) correspondent deux valeurs de \(x\) ; par conséquent elle n’admet pas de fonction réciproque.
Par contre, si on réduit l’ensemble de définition soit à \({\mathbb{R}^ * }\) (\(\left[ {0; + \infty } \right[\)) soit à \({\mathbb{R}^ - }\) (\(\left] { - \infty ;0} \right]\)), la même fonction \(f\) devient bijective, et admet alors une fonction réciproque.
Par convention, on choisit \(I = {\mathbb{R}^ + }\), et on appelle racine carrée de \(x\), notée $x $ cette fonction réciproque. D’où :
\(\left. \begin{gathered} y = {x^2}\\ x \geqslant 0\\ \end{gathered} \right \} \Leftrightarrow x = \sqrt y\)
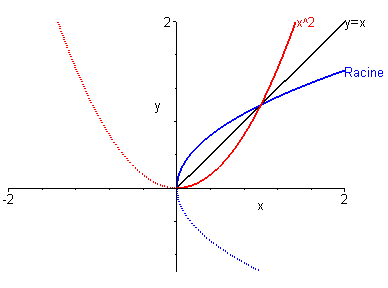
Une méthode fort ancienne (que l’on doit à Héron d’Alexandrie) permet d’extraire la racine carrée d’un nombre quelconque par un procédé itératif, autrement dit « comment calcule-t-on rapidement une racine carrée lorsque les batteries de la calculette sont épuisées? ».
4 Fonctions majorées, minorées, bornées - Extremums
4.1 Comparer, majorer, minorer des nombres réels
4.1.1 Comparaison de deux réels
Pour comparer deux réels, on peut procéder de trois manières différentes :
- On peut étudier le signe de leur différence \(A - B\) :
\(A \geqslant B \Leftrightarrow A - B \geqslant 0\)
- S’ils sont strictement positifs, on peut comparer leur quotient \(\frac{A}{B}\) à * :
\(A \geqslant B \Leftrightarrow \frac{A}{B} \geqslant 1\)
- On peut utiliser les variations des fonctions usuelles (voir chapitre 1, paragraphe 5)
4.1.2 Majorer la somme \(A + B\) ou le produit \(AB\)
Il suffit dans ce cas de majorer \(A\) ou B :
Si \(A \leqslant M\), alors \(A + * \leqslant M + B\)
Si \(A \leqslant M\) et \(B > 0\), alors \(A.B \leqslant M.B\)
4.1.3 Majorer le quotient \(\frac{A}{B}\)
On suppose ici que \(A \geqslant 0\) et que \(B > 0\). Pour majorer le quotient \(\frac{A}{B}\), il suffit de majorer le numérateur \(A\) ou de minorer le dénominateur \(B\) par un nombre réel strictement positif :
Si \(A \leqslant M\), alors \(\frac{A}{B} \leqslant \frac{M}{B}\)
Si \(B \geqslant m\), alors \(\frac{A}{B} \leqslant \frac{A}{m}\)
4.2 Comparer, majorer, minorer des fonctions réelles
Définition :
Pour toutes fonctions \(f:I \to \mathbb{R}\) et \(g:I \to \mathbb{R}\), \(f \leqslant g\) signifie que \(\forall x \in I{\text{, }}f\left( x \right) \leqslant g\left( x \right)\).
Définitions :
Soit \(f:I \to \mathbb{R}\).
On dit que \(f\) est majorée, s’il existe un réel \(M\) tel que \(\forall x \in I,{\text{ }}f\left( x \right) \leqslant M\). Dans ce cas, on appelle borne supérieure de \(f\) sur l’intervalle \(I\), noté \(\mathop {\sup }\limits_I f\), le plus petit majorant de \(f\).
On dit que \(f\) est minorée, s’il existe un réel \(m\) tel que \(\forall x \in I,{\text{ }}f\left( x \right) \geqslant m\). Dans ce cas, on appelle borne inférieure de \(f\) sur l’intervalle \(I\), noté \(\mathop {\inf }\limits_I f\), le plus grand minorant de \(f\).
On dit que \(f\) est bornée, si \(f\) est à la fois majorée et minorée. \(f\) est donc bornée s’il existe deux réels \(M\) et \(m\) tels que \(\forall * \in I,{\text{ }}m \leqslant f\left( x \right) \leqslant M\).
Remarques : Soient \(f:I \to \mathbb{R}\) et \(g:I \to \mathbb{R}\).
\(f\) est bornée si et seulement si \(\left| f \right|\) est majorée.
Si \(f\) et \(g\) sont majorées, alors \(f + g\) est majorée : \(\mathop {\sup }\limits_I \left( {f * g} \right) \leqslant \mathop {\sup }\limits_I f + \mathop {\sup }\limits_I g\)
Si \(f\) et \(g\) sont minorées, alors \(f + g\) est minorée : \(\mathop {\inf }\limits_I \left( {f * g} \right) \geqslant \mathop {\inf }\limits_I f + \mathop {\inf }\limits_I g\)
\(f\) est majorée (respectivement minorée) si et seulement si \(\left( - f} \right)\) est minorée (resp. majorée) : \(\mathop {\sup }\limits_I \left( { - f} \right) = - \mathop {\inf }\limits_I f\) (resp. \(\mathop {\inf }\limits_I \left( { - f} \right) = - \mathop {\sup }\limits_I f\)).
Soit un réel \(\alpha > 0\). Si \(f\) est majorée (respectivement minorée), alors \(\alpha f\) est majorée (respectivement minorée) : \(\mathop {\sup }\limits_I \left( {\alpha f} \right) = \alpha \mathop {\sup }\limits_I f\) (\(\mathop {\inf }\limits_I \left( {\alpha f} \right) = \alpha \mathop {\inf }\limits_I f\)).
Si \(f\) et \(g\) sont bornées, alors \(\forall \left( {\alpha ,\beta } \right) \in {\mathbb{R}^2}\), \(\alpha f + \beta g\) est bornée.
Exemple :
Soit la fonction définie sur \(\mathbb{R}\) par \(f\left( x \right) = \frac{4}{{{x^2} + 4}}\).
\(f\) est-elle bornée ? Si oui, quelles sont ses bornes inférieure et supérieure ? Réponse
4.3 Extremums
Définition :
Soit \(f:I \to \mathbb{R}\). Soit \({x_0} \in \mathbb{R}\).
On dit que \(f\) présente un maximum global en \({x_0}\) si \(\forall * \in I{\text{, }}f\left( x \right) \leqslant f\left( {{x_0}} \right)\).
On dit que \(f\) présente un minimum global en \({x_0}\) si \(\forall * \in I{\text{, }}f\left( x \right) \geqslant f\left( {{x_0}} \right)\).
Dans l’un de ces deux cas, on dit que \(f\) présente un extremum global en \({x_0}\).
Remarques :
- \(f\) présente un maximum global en \({x_0}\) $ \($f\) est majorée sur \(I\) et \(\mathop {\sup }\limits_I f = f\left( {{x_0}} \right)\). On note alors \(f\left( {{x_0}} \right) = \mathop {\max }\limits_I f\). On dit que f atteint sa borne supérieure en \({x_0}\).
- \(f\) présente un minimum global en \({x_0}\) $ \($f\) est minorée sur \(I\) et \(\mathop {\inf }\limits_I f = f\left( {{x_0}} \right)\). On note alors \(f\left( {{x_0}} \right) = \mathop {\min }\limits_I f\). On dit que f atteint sa borne inférieure en \({x_0}\).
5 Variation des fonctions
5.1 Fonctions croissantes, décroissantes, monotones
Définitions :
Soit \(f:I \to \mathbb{R}\).
On dit que \(f\) est croissante sur \(I\) si \(\left\{ {\left( {x,y} \right) \in {I^2}{\text{ et }}x \leqslant y} \right\}\), $ $ \(f\left( x \right) \leqslant f\left( * \right)\).
On dit que \(f\) est décroissante sur \(I\) si \(\left\{ {\left( {x,y} \right) \in {I^2}{\text{ et }}x \leqslant y} \right\}\), $ $ \(f\left( x \right) \geqslant f\left( * \right)\).
On dit que \(f\) est strictement croissante sur \(I\) si \(\left\{ {\left( {x,y} \right) \in {I^2}{\text{ et }}x < y} \right\}\), $ $ \(f\left( x \right) < f\left( y \right)\).
On dit que \(f\) est strictement décroissante sur \(I\) si \(\left\{ {\left( {x,y} \right) \in {I^2}{\text{ et }}x < y} \right\}\), $ $ \(f\left( x \right) > f\left( y \right)\).
On dit que \(f\) est (strictement) monotone sur \(I\) si elle est (strictement) croissante ou (strictement) décroissante sur \(I\).
Exemple :
Considérons la fonction définie sur \(\mathbb{R}\) par \(f\left( x \right) = {x^2}\).
Montrer que la fonction \(f\) est strictement décroissante sur \({\mathbb{R}^{ * - }} = \left] { - \infty ;0} \right[\) et strictement croissante sur \({\mathbb{R}^{ * + }} = \left] {0; * \infty } \right[\). Réponse
5.2 Somme et produit de fonctions monotones
Définition :
Soit \(f:I \to \mathbb{R}\). On dit que \(f\) est positive (respectivement négative), si \(\forall * \in I\), \(f\left( x \right) \geqslant 0\) (respectivement \(f\left( x \right) \leqslant 0\)).
Propositions : Soient \(f:I \to \mathbb{R}\) et \(g:I \to \mathbb{R}\).
Si \(f\) et \(g\) ont même monotonie, alors \(f + g\) est monotone de même monotonie.
Si de plus \(f\) ou \(g\) est strictement monotone, alors \(f + g\) est strictement monotone.Si \(f\) et \(g\) sont positives croissantes, alors \(fg\) est positive croissante ;
Si \(f\) et \(g\) sont positives décroissantes, alors \(fg\) est positive décroissante.Si \(f\) et \(g\) sont négatives croissantes, alors \(fg\) est positive décroissante ;
Si \(f\) et \(g\) sont négatives décroissantes, alors \(fg\) est positive croissante.Si \(f\) est positive croissante et \(g\) négative décroissante, alors \(fg\) est négative décroissante ;
Si \(f\) est positive décroissante et \(g\) négative croissante, alors \(fg\) est négative croissante.
Exemple :
Soit \(f\) définie par \(f\left( x \right) = \frac{1}{{{x^2}}}\) positive décroissante sur \(\left] {0; + \infty } \right[\) (voir proposition suivante) et \(g\) définie par \(g\left( x \right) = - \frac{1}{x}\) négative croissante sur \(\left] {0; + \infty } \right[\). Alors \(\left( {fg} \right)\left( x \right) = - \frac{1}{{{x^3}}}\) est négative croissante sur \(\left] {0; + \infty } \right[\).
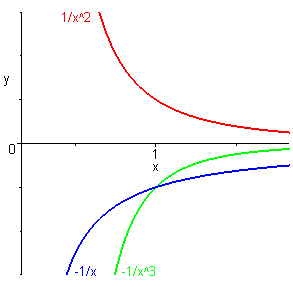
Remarques :
- Cas d’indétermination sur le produit de deux fonctions :
| \(f\) | \(g\) | \(fg\) |
|---|---|---|
| Positive croissante | Positive décroissante | ? |
| Positive décroissante | Négative décroissante | ? |
| Positive croissante | Négative croissante | ? |
| Négative croissante | Négative décroissante | ? |
Si \(\alpha \geqslant 0\), alors \(\alpha f\) et \(f\) ont même monotonie ;
Si \(\alpha \leqslant 0\), alors \(\alpha f\) et \(f\) sont de monotonie contraire ; c’est le cas de \(\left( { - f} \right)\) et \(f\).
5.3 Inverse d’une fonction monotone
Proposition :
Soit \(f:I \to \mathbb{R}\) monotone. Si on suppose que \(f\) ne s’annule jamais sur \(I\), et qu’elle est de signe constant, alors la fonction inverse \(\left( {\frac{1}{f}} \right)\) est monotone sur \(I\), de monotonie contraire à celle de \(f\) et de même signe.
Exemples :
On retrouve le résultat de l’exercice précédent en prenant \(f\left( x \right) = {x^2}\).
Soit la fonction \(f\) définie par \(f\left( x \right) = {x^2} + 1\). \(f\) est positive strictement croissante sur \(\left[ {0; + \infty } \right[\) et ne s’y annule jamais. Par conséquent, \(\left( {\frac{1}{f}} \right)\left( * \right) = \frac{1}{{{x^2} + 1}}\) est strictement décroissante sur \(\left[ {0; + \infty } \right[\). On peut faire le même raisonnement sur \(\left] { - \infty ;0} \right]\).

5.4 Composition de fonctions monotones
Proposition
Soient deux fonctions, \(f\) définie sur un intervalle \(I \subseteq \mathbb{R}\) et \(g\) définie sur un intervalle \(J \subseteq \mathbb{R}\), telles que \(\forall * \in I,f\left( x \right) \in J \left[ {f\left( I \right) \subseteq j} \right]\).
Si \(f\) et \(g\) ont même monotonie, l’une sur \(I\) et l’autre sur \(J\), alors la composée \(g \circ f\) est croissante sur \(I\).
Si \(f\) et \(g\) sont de monotonie contraire, l’une sur \(I\) et l’autre sur \(J\), alors la composée \(g \circ f\) est décroissante sur \(I\).
Exemple
Soit la fonction \(h\) définie sur l’intervalle \(\left[-2;2\right]\) par $h( x ) = $.
Montrer que la fonction \(h\) est croissante sur \(\left[-2;0\right]\), et décroissante sur \(\left[0;2\right]\). Réponse
6 Fonctions paires, impaires, périodiques
6.1 Fonctions paires et impaires
Soit une fonction \(f\), définie sur une partie \(D\) de \(\mathbb{R}\) symétrique par rapport à 0 (\(x \in D \Leftrightarrow - x \in D\)).
Définition :
On dit que \(f\) est paire si \(\forall * \in D\), \(f\left( { - x} \right) = f\left( x \right)\)
On dit que \(f\) est impaire si \(\forall * \in D\), \(f\left( { - x} \right) = - f\left( * \right)\)
Remarque : la seule fonction à la fois paire et impaire est la fonction nulle. En effet, \(\forall x \in D\), \(f\left( x \right) = f\left( { - x} \right) = - f\left( x \right)\), donc \(f\left( x \right) = 0\).
Proposition :
Toute somme finie de fonctions impaires est une fonction impaire.
Toute somme finie de fonctions paires est une fonction paire.
Exemple :
Soit \(f\left( x \right) = {x^2} + 1\) et \(g\left( * \right) = - \frac{1}{{{x^2}}}\).
\(f\) et \(g\) sont des fonctions paires, leur somme définie par \(h\left( x \right) = {x^2} + 1 - \frac{1}{{{x^2}}}\) est aussi une fonction paire.

Propositions : Soient \(f\) et \(g\) définies sur une partie \(D\) de \(\mathbb{R}\) symétrique par rapport à 0 (\(x \in D \Leftrightarrow - x \in D\)).
Si \(f\) et \(g\) ont même parité, fg est paire. Si elles sont de parité contraire, fg est impaire.
L’application \(\frac{1}{f}\), si elle existe, est de même parité que \(f\).
Soit \(\left( {\alpha ,\beta } \right) \in {\mathbb{R}^2}\). Si \(f\) et \(g\) sont paires (respectivement impaires), \(\alpha * + \beta g\) est paire (respectivement impaire).
Si \(f\) est bijective de \(D\) dans \(D\) (\(D \subseteq \mathbb{R}\)) et impaire, alors sa bijection réciproque \({f^{ * 1}}\) est impaire.
Si \(f\) est paire, alors \(h \circ f\) est paire quelque soit la fonction \(h\).
Si \(f\) est impaire, et si g paire ou impaire, alors \(g \circ f\) à la même parité que \(g\).
Exemple :
Soit \(f\left( x \right) = {x^3}\). \(f\) est impaire et bijective sur \(\mathbb{R}\).
Sa fonction réciproque \(g\left( x \right) = \sqrt[3]{x}\) est impaire sur \(\mathbb{R}\).
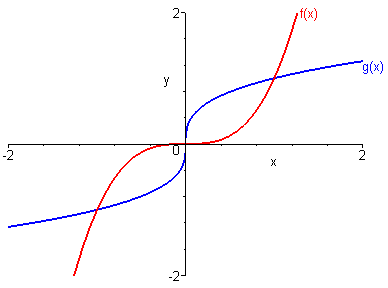
6.2 Fonctions périodiques
Définition :
Soit \(f:{D_f} \to \mathbb{R}\). S’il existe \(T \in \mathbb{R}\) strictement positif tel que \(\forall x \in {D_f}\), \(x * T \in {D_f}\) et \(f\left( {x + T} \right) = f\left( x \right)\), alors la fonction \(f\) est dite périodique de période \(T\). On dit aussi que \(f\) est \(T\)-périodique.
Propriétés :
Si \(f\) est \(T\)-périodique, alors \(\forall n \in \mathbb{Z}\), \(f\) est \(nT\)-périodique.
Si \(f\) et g sont \(T\)-périodiques, alors \(\alpha f + \beta g\) est \(T\)-périodique, \(\forall \left( {\alpha ,\beta } \right) \in {\mathbb{R}^2}\).
Si \(f\) est \(T\)-périodique, alors la fonction \(\frac{1}{f}\), si elle existe, est \(T\)-périodique.
Si \(f\) est \(T\)-périodique, alors, quelque soit la fonction \(g\), \(g \circ f\) est \(T\)-périodique.
Exemple :
Les fonctions sinus et cosinus sont $2$-périodiques.

6.3 Axes et centres de symétrie
6.3.1 Graphes symétriques par rapport à l’origine
Soit \(f\) une fonction définie sur un domaine \(D\) de \(\mathbb{R}\) symétrique par rapport à 0 (\(x \in D \Leftrightarrow - x \in D\)).
\(f\) est impaire si et seulement si son graphe est symétrique par rapport à l’origine.
Pour \(x = 0\), et si \(f\left( 0 \right)\) existe, on a \(f\left( { - 0} \right) = - f\left( 0 \right)\), d’où \(f\left( 0 \right) = - f\left( 0 \right)\) et donc \(f\left( 0 \right) = 0\).
Ceci signifie que le graphe d’une fonction impaire qui est définie en 0 passe nécessairement par l’origine.
Exemples :
\(f\left( x \right) = {x^3}\)
\(f\left( x \right) = \sin x\)
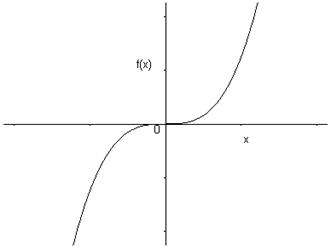
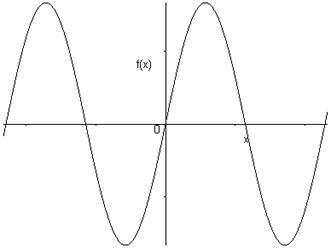
6.3.2 Graphes symétriques par rapport à Oy
Dans un repère orthonormé, soit une fonction \(f\), définie sur un domaine \(D\) de \(\mathbb{R}\) symétrique par rapport à 0 (\(x \in D \Leftrightarrow - x \in D\)).
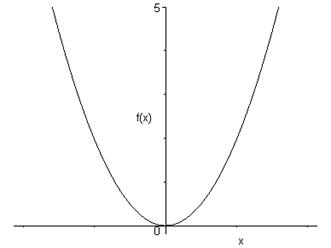
\(f\) est paire si et seulement si son graphe est symétrique par rapport à \(Oy\).
Exemples :
\(f\left( x \right) = {x^2}\)
\(f\left( x \right) = \cos x\)
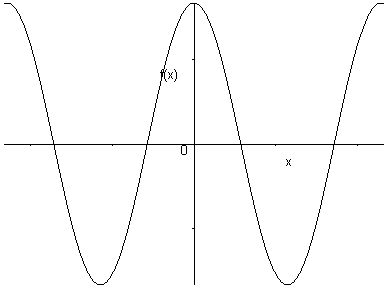
6.3.3 Graphes périodiques
Soit \(f:D \to \mathbb{R}\), le domaine étant tel que \(x \in D \Rightarrow x + T \in D\) (\(T > 0\) donné).
\(f\) est T-périodique si et seulement si son graphe est invariant par une translation de vecteur \(\left( {kT,0} \right)\) avec \(k \in \mathbb{Z}\).
Exemple :
Soit \(f\left( x \right) = \tan x\)
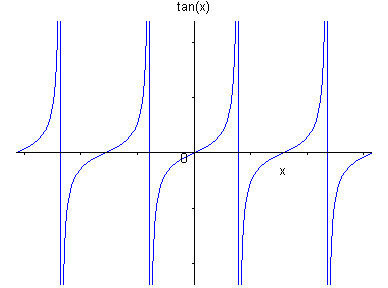
6.3.4 Graphe de la fonction réciproque
Soit \(f\) une application bijective de \(D\) sur \(f\left( * \right)\).
Les graphes des fonctions \(f\) et \({f^{ * 1}}\) sont symétrique par rapport à la droite \(y = x\).
Voir § 3.3.2. chapitre 1
6.3.5 Conséquences pratiques : Réduction de l’intervalle d’étude
Soit une fonction \(f\), définie sur un domaine \(D\) de \(\mathbb{R}\) symétrique par rapport à 0.
Si \(f\) est paire (ou impaire), on peut réduire l’intervalle d’étude aux \(x\) positifs. Le graphe de la fonction sur \(D\) se déduira par symétrie par rapport à Oy (ou 0).
Si \(f\) est \(T\)-périodique, on peut réduire l’intervalle d’étude à la seule période \(T\). Le graphe de la fonction sur \(D\) se déduira par des translations de \(T\) le long de l’axe des \(x\).
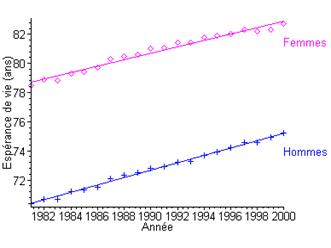
7 Un exemple d’application en Biologie
D’après les informations diffusées par l’Institut National des Etudes Démographiques (INED), il semble que l’espérance de vie à la naissance des hommes et des femmes augmente en fonction du temps depuis ces vingt dernières années.
Ainsi, si on désigne par \(t\) l’année et par \(E\) l’espérance de vie à la naissance, alors :
$E = t + $
où les coefficients $$ et $$ dépendent du sexe. *
Par exemple :
\({E_{femmes}} = 0.221t - 358\)
\({E_{hommes}} = 0.253t - 432\) *
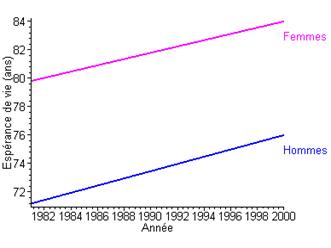
Pour ce qui suit, vous pourrez vous référer au cours de probabilités et statistiques pour en savoir plus…
Des données publiées par l’INED fournissent pour la France des valeurs moyennes de l’espérance de vie à la naissance des hommes et des femmes, estimées chaque année depuis 1981. On peut ainsi représenter les couples \(\left( {{t_i},{E_i}} \right)\) pour \(i\) variant de 1 à 20 :
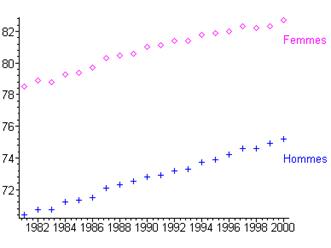
figure
On peut vérifier par ajustement que l’on a bien la relation supposée au départ entre \(E\) et t :