Chapitre 5 — Produit scalaire et norme
Sandrine CHARLES : scharles@biomserv.univ-lyon1.fr
Introduction
La notion d’espace vectoriel constitue le cadre général de l’Algèbre Linéaire. La richesse de cette théorie s’accroît si on y ajoute d’autres structures. La plus importante d’entre elles fait référence aux mesures de longueurs, de distance et d’angle : c’est la structure métrique. Et c’est la notion de produit scalaire qui permet de donner un sens, de définir, et d’étudier les propriétés métriques d’un espace vectoriel.
1 Produit scalaire
Définition 1
Soit $$ une application de \(E \times E\) dans \[\mathbb{R}\] qui a tout couple \(\left( {\vec u,\vec v} \right)\) de vecteurs de \(E\) fait correspondre un réel \(\varphi \left( {\vec u,\vec v} \right)\). $$ est une forme bilinéaire, si elle est linéaire par rapport à \(\vec u\) et par rapport à \(\vec v\) :
\(\forall {\vec u_1},{\vec u_2} \in E{\text{, }}\forall \vec v \in E{\text{, }}\forall \lambda ,\mu \in \mathbb{R}\) \(\varphi \left( {\lambda {{\vec u}_1} + \mu {{\vec u}_2},\vec v} \right) = \lambda \varphi \left( {{{\vec u}_1},\vec v} \right) + \mu \varphi \left( {{{\vec u}_2},\vec v} \right)\)
\(\forall \vec u \in E{\text{, }}\forall {\vec v_1},{\vec v_2} \in E{\text{, }}\forall \lambda ,\mu \in \mathbb{R}\) \(\varphi \left( {\vec u,\lambda {{\vec v}_1} + \mu {{\vec v}_2}} \right) = \lambda \varphi \left( {\vec u,{{\vec v}_1}} \right) + \mu \varphi \left( {\vec u,{{\vec v}_2}} \right)\)
Remarque
Cette définition rejoint celle des formes multilinéaires introduite pour les déterminants.
Proposition 1
$$ est symétrique si \(\forall \vec u,\vec v \in E{\text{, }}\varphi \left( {\vec u,\vec v} \right) = \varphi \left( {\vec v,\vec u} \right)\)
$$ est définie si \(\forall \vec u \in E{\text{, }}\varphi \left( {\vec u,\vec u} \right) = 0 \Rightarrow \vec u = \vec 0\)
$$ est positive si \(\forall \vec u \in E{\text{, }}\varphi \left( {\vec u,\vec u} \right) \geqslant 0\) *
Définition 2
On appelle produit scalaire une forme bilinéaire symétrique, définie et positive.
Notations du produit scalaire : \(\varphi \left( {\vec u,\vec v} \right)\quad \quad \left( {\begin{array}{*{20}{c}}\)
- {u}&& {v}$
\(\end{array}} \right)\quad \quad \left\langle {\vec u,\vec v} \right\rangle \quad \quad \vec u \bullet \vec v\)
Dans toute la suite du cours nous adopterons la notation \(\vec u \bullet \vec v\).
Remarques
· Un espace vectoriel est muni a priori de plusieurs produits scalaires.
· \(\vec u \bullet \vec v\) est une opération entre deux vecteurs ; le résultat est un scalaire.
Définition 3
Un espace vectoriel muni d’un produit scalaire est appelé espace préhilbertien.
D’après la définition du produit scalaire, \(\vec u \bullet \vec u\) est positif ou nul ; Il admet donc une racine carrée que l’on note ${| {u} |_ } = $.
Définition
On appelle norme ou longueur du vecteur \(\vec u\) associée au produit scalaire (•) et notée \({\left\| {\vec u} \right\|_ \bullet }\), le scalaire :
\({\left\| {\vec u} \right\|_ \bullet } = \sqrt {\vec * \bullet \vec u} \Leftrightarrow \left\| {\vec u} \right\|_ \bullet ^2 = \vec * \bullet \vec u\)
1.1 Le produit scalaire canonique de \[{\mathbb{R}^n}\]
On rappelle que \[{\mathbb{R}^n}\] est un espace vectoriel.
Proposition
L’application suivante est un produit scalaire :
\(\begin{array}{*{20}{l}}\)
{:}&{{^n} }& &&{{}x = ( {{x_1}, ,{x_n}} ){}y = ( {{y_1}, ,{y_n}} )} \$
{}&{( {x,y} )}& &{_{i = 1}^{i = n} {{x_i}{y_j}} }&{}$
\(\end{array}\)
On l’appelle produit scalaire canonique de \[{\mathbb{R}^n}\].
Définition
L’espace vectoriel \[{\mathbb{R}^n}\] muni de son produit scalaire canonique est appelé espace euclidien de dimension \(n\).
è Dans toute la suite du chapitre, nous ferons toujours référence pour \[{\mathbb{R}^n}\], sauf mention contraire, au produit salaire canonique.
Remarque
Si on désigne par \[{\mathbf{X}}\] et \[{\mathbf{Y}}\] les matrices des coordonnées des vecteurs \(\vec x = \left( {{x_1}, \ldots ,{x_n}} \right)\) et \(\vec * = \left( {{y_1}, \ldots ,{y_n}} \right)\), alors on a \[\boxed{\vec x \bullet \vec y = {}^t{\mathbf{XY}}}\].
Exemple
Soient \(\vec x\; = \left( {1, - 2,5} \right)\) et \(\vec y\; = \left( {2, - 1,3} \right)\) deux vecteurs de \[{\mathbb{R}^3}\] muni de son produit scalaire canonique. Vérifier la proposition précédente. Réponse.
Proposition
\[{\mathbb{R}^n}\] étant muni de son produit scalaire canonique, la norme de \(\vec x \in {\mathbb{R}^n}\) s’écrit :
\({\left\| {\vec x} \right\|^2} = \sum\limits_{i = 1}^n {x_i^2} \Leftrightarrow {\left\| {\vec x} \right\|^2} = \vec x \bullet \vec x = {}^t{\mathbf{XX}}\)
Exemple
On suppose \[{\mathbb{R}^3}\] muni de son produit scalaire canonique. Calculer la norme de \(\vec x\; = \left( {2, - 2, - 1} \right)\). Normer \(\vec x\). Réponse.
1.2 D’autres exemples
1. Soit \(V\) l’ensemble des fonctions continues sur l’intervalle \[\left[ {a,b} \right]\]. \(V\) est un espace vectoriel.
Alors l’expression suivante définit un produit scalaire sur \(V\) :
\[f \bullet g * \int\limits_a^b {f\left( t \right)g\left( t \right)dt} \]
Où \(f\) et \(g\) sont des fonctions quelconques continues sur \[\left[ {a,b} \right]\].
2. Considérons \[{M_{n,p}}\left( \mathbb{R} \right)\] l’ensemble des matrices de dimension \[\left( {n,p} \right)\] à coefficients dans \[\mathbb{R}\]. Nous avons déjà vu que \[{M_{n,p}}\left( \mathbb{R} \right)\] est un espace vectoriel (Chap3, § 2.2).
Alors l’expression suivante définit un produit scalaire sur \[{M_{n,p}}\left( \mathbb{R} \right)\] :
\[{\mathbf{A}} \bullet {\mathbf{B}} = tr\left( {{}^t{\mathbf{AB}}} \right)\]
où tr désigne la trace de la matrice \[{}^t{\mathbf{AB}}\] c’est-à-dire la somme des éléments diagonaux de la matrice. Si \[{\mathbf{A}} * \left[ {{a_{ij}}} \right]\] et \[{\mathbf{B}} * \left[ {{b_{ij}}} \right]\] avec \[i = 1,n\] et \[j = 1,p\], alors :
\[{\mathbf{A}} \bullet {\mathbf{B}} = tr\left( {{}^t{\mathbf{AB}}} \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^p {{a_{ij}}{b_{ij}}} } \]
2 Inégalité de Cauchy-Schwartz et applications
Théorème 1 (Inégalité de Schwartz)
Si $ $ est un produit scalaire sur un espace vectoriel \(E\), pour tout \[\vec u,\vec v \in E\] :
$| {u v} | $ ce qui équivaut à \(\left| {\vec u \bullet \vec v} \right| \leqslant {\left\| {\vec u} \right\|_ \bullet }{\left\| {\vec v} \right\|_ \bullet }\)
Remarque
Le symbole \[\left| {{\text{ }}} \right|\] désigne la valeur absolue.
Théorème 2
Soit \(E\) un espace préhilbertien. Alors la norme de \(E\) satisfait les propriétés suivantes :
\({\left\| {\vec u} \right\|_ \bullet } \geqslant 0\) et \({\left\| {\vec u} \right\|_ \bullet } = 0 \Leftrightarrow \vec u = \vec 0\)
\({\left\| {\lambda \vec u} \right\|_ \bullet } = \left| \lambda \right|\;{\left\| {\vec u} \right\|_ \bullet }\quad \left( {\lambda \in \mathbb{R}} \right)\)
\({\left\| {\vec u + \vec v} \right\|_ \bullet } \leqslant {\left\| {\vec u} \right\|_ \bullet } + {\left\| {\vec v} \right\|_ \bullet }\)
Remarque
La propriété (iii) est appelée « inégalité triangulaire » car si on considère \[\vec u * \vec v\] comme troisième côté du triangle formé avec \[\vec u\] et \[\vec v\], alors (iii) signifie que la longueur d’un côté du triangle est inférieure ou égale à la somme des longueurs des deux autres côtés.
Définition
Soit \(E\) un espace préhilbertien. Soit \[\vec u \in E\]. Si \[{\left\| {\vec u} \right\|_ \bullet } = 1\], ou si de manière équivalente \[\vec u \bullet \vec u = 1\], alors \[\vec u\] est appelé un vecteur unitaire.
Proposition
Si \(\vec x \ne {\vec 0_E}\) un vecteur quelconque de \(E\) espace préhilbertien, alors le vecteur \(\vec u = \frac{1}{{\left\| {\vec x} \right\|}}\vec x\) est unitaire et colinéaire à \(\vec x\). On appelle \(\vec u\) le vecteur normé associé à \(\vec x\). Le procédé correspondant s’appelle la normalisation.
Remarque
Quels que soient les vecteurs \[\vec u,\vec v \in E\], l’angle que font entre eux les vecteurs \[\vec u\] et \[\vec v\] est l’angle \[\theta \] tel que \[0 \leqslant \theta \leqslant \pi \] et :
\(\cos \theta = \frac{{\vec * \bullet \vec v}}{{{{\left\| {\vec u} \right\|}_ \bullet }{{\left\| {\vec v} \right\|}_ \bullet }}}\)
D’après l’inégalité de Cauchy-Schwartz, \[ - 1 \leqslant \cos \theta \leqslant 1\], et donc l’angle \[\theta \] existe toujours et est unique.
Représentation graphique
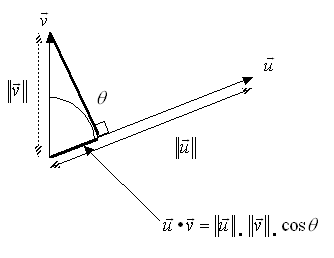
Unnamed Image
3 Orthogonalité, projection
3.1 Définition
Définition
Soit \(E\) un espace préhilbertien. Deux vecteurs \(\vec u\) et \(\vec v\) de \(E\) sont dits orthogonaux si et seulement si :
\(\vec u \bullet \vec v = 0\)
On dit aussi que \(\vec u\) est orthogonal à \(\vec v\).
Remarques
« \[\vec 0 \in E\] est orthogonal à tout vecteur \[\vec u \in E\]. En effet, \(\vec 0 \bullet \vec u = \left( {0\vec u} \right) \bullet \vec u = 0\left( {\vec u \bullet \vec u} \right) = 0\).
« Inversement, si \(\vec u\) est orthogonal à tout vecteur de \(E\), alors \(\vec u = \vec 0\). En effet, si \(\vec u\) est orthogonal à tout vecteur de \(E\), alors en particulier \[\vec * \bullet \vec u = 0\] et donc \(\vec u = \vec 0\).
« \(\vec u\) est orthogonal à \(\vec v\) si et seulement si \[\cos \theta = 0\], c’est-à-dire si et seulement si \[\theta = \pm \frac{\pi }{2}\].
3.2 Recherche de vecteurs orthogonaux
Dans le plan, il est parfois utile de savoir trouver rapidement les coordonnées d’un vecteur \(\vec v\) orthogonal à un vecteur quelconque \(\vec * = \;\left( {{u_1},{u_2}} \right)\).
Soit \(\vec v\; = \left( {{v_1},{v_2}} \right)\) orthogonal à \(\vec u\). Alors \(\vec u \bullet \vec v = 0 \Leftrightarrow {u_1}{v_1} + {u_2}{v_2} = 0\). Si on suppose \({u_1} \ne 0\), alors on a \({v_1} = - \frac{{{u_2}}}{{{u_1}}}{v_2}\). L’ensemble des vecteurs orthogonaux à \(\vec u\) est donc défini comme :
\(\left\{ {{{\vec v = \left( {{v_1},{v_2}} \right) \in {\mathbb{R}^2}} \mathord{\left/\)
\({\vphantom {{\vec v = \left( {{v_1},{v_2}} \right) \in {\mathbb{R}^2}} {{v_1} = - \frac{{{u_2}}}{{{u_1}}}{v_2}}}} \right.\)
\(\kern-\nulldelimiterspace} {{v_1} = - \frac{{{u_2}}}{{{u_1}}}{v_2}}}} \right\}\)
En particulier, si on pose \({v_1} * - {u_2}\), alors \(\vec v\; = \left( * - {u_2},{u_1}} \right)\) est orthogonal à \(\vec u\; = \left( {{u_1},{u_2}} \right)\). De même, \(\vec v = \;\left( {{u_2}, - {u_1}} \right)\) est orthogonal à \(\vec u\; = \left( {{u_1},{u_2}} \right)\).
Exemple
Soit \(\vec u = \;\left( {1,3} \right)\). Alors \(\vec v = \;\left( { - 3,1} \right)\) est orthogonal à \(\vec u\) : \(\left( {\begin{array}{*{20}{c}}\)
- 1&3$
\(\end{array}} \right)\left( {\begin{array}{*{20}{c}}\)
{ - 3} \$
1$
\(\end{array}} \right) = - 3 * 3 = 0\).
3.4 Ensembles orthogonaux
Définitions
« Un ensemble \[F = \left\{ {{{\vec u}_1}, \ldots ,{{\vec u}_p}} \right\}\] de vecteurs de \(E\), un espace préhilbertien, est dit orthogonal si deux vecteurs quelconques de \(F\) sont orthogonaux : \[{\vec u_i} \bullet {\vec u_j} = 0\], \[\forall i \ne j\]
\(«\)\(F\) est dit orthonormal, si \(F\) est orthogonal et si tous les vecteurs de \(F\) sont unitaires : \(${\vec u_i} \bullet {\vec u_j} * {\delta _{ij}} = \left\{ {\begin{array}{*{20}{c}}\)
\(«\)\(0&{{\text{si }}i \ne j} \\\)
\(«\)\(1&{{\text{si }}i = j}\)
« \(\end{array}} \right.\)$
Remarque
On peut normaliser un ensemble orthogonal en normalisant chacun des vecteurs.
Théorème 1
Soit \(F\) un ensemble orthogonal de vecteurs non nuls. Alors les vecteurs de \(F\) sont linéairement indépendants.
Théorème * : Pythagore
Soit \[F = \left\{ {{{\vec u}_1}, \ldots ,{{\vec u}_p}} \right\}\] un ensemble orthogonal. Alors :
\[\left\| {{{\vec u}_1} * \ldots + {{\vec u}_p}} \right\|_ \bullet ^2 = \left\| {{{\vec u}_1}} \right\|_ \bullet ^2 + \ldots + \left\| {{{\vec u}_p}} \right\|_ \bullet ^2\]
Remarque
Ce dernier théorème permet de retrouver le théorème de Pythagore dans le cas du plan. En effet, si on considère deux vecteurs \[\vec u\] et \[\vec v\] du plan tels que \[\vec u \bullet \vec * = 0\], alors :
\(\begin{gathered}\)
{| {u + v} |^2} = ( {u + v} ) ( {u + v} ) \$
= ( {u u} ) + 2( {u v} ) + ( {v v} ) \$
= ( {u u} ) + ( {v v} ) \$
= {| {u} |^2} + {| {v} |^2} \$
$\end{gathered} $
Proposition
La base canonique \(B = \left\{ {{{\vec e}_1},{{\vec e}_2}, \ldots ,{{\vec e}_n}} \right\}\) de l’espace euclidien \[{\mathbb{R}^n}\] est une base orthonormale. En effet, \(\forall i \ne j\quad {\vec e_i} \bullet {\vec e_j} = 0\) et \(\forall i = 1,n\quad {\left\| {{{\vec e}_i}} \right\|_ \bullet } = 1\). *
3.5 Projecteur orthogonal
Soit \[{\mathbb{R}^n}\] espace euclidien. Considérons une direction définie par un vecteur \[\vec u \in {\mathbb{R}^n}\]. Soit \[\vec v \in {\mathbb{R}^n}\]. Cherchons à caractériser la projection orthogonale de \[\vec v\] sur la direction définie par \[\vec u\] :[
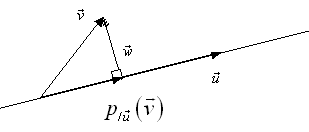
Unnamed Image
On cherche donc à caractériser le vecteur \({p_{/\vec u}}\left( {\vec v} \right)\) par rapport au vecteur \[\vec v\].
Soit \[\vec w\] et \[{p_{/\vec u}}\left( {\vec v} \right)\] tels que par construction l’on ait :
\[\vec v = \vec w + {p_{/\vec u}}\left( {\vec v} \right) \Leftrightarrow \vec w = \vec v - {p_{/\vec u}}\left( {\vec v} \right)\]
Or \[{p_{/\vec u}}\left( {\vec v} \right)\] est colinéaire à \[\vec u\] donc il peut s’écrire \[{p_{/\vec u}}\left( {\vec v} \right) = \lambda \vec u\].
D’autre part, la caractéristique fondamentale de \[{p_{/\vec u}}\left( {\vec v} \right)\] est que \[\vec w\] est orthogonal à \[\vec u\] :
\($\begin{gathered}\)
w u = 0 u = 0 \$
w u = 0 ( {v} ) u = v u \$
w u = 0 = v u \$
w u = 0 = v u \$
w u = 0 = v u \$
w u = 0 \$
$\end{gathered} $$
Définition 1
Soient \[\vec u\] et \[\vec v\] deux vecteurs non nuls de \[{\mathbb{R}^n}\]. Le vecteur projeté de \[\vec v\] sur \[\vec u\] est le vecteur : * \[{p_{/\vec u}}\left( {\vec v} \right) = \frac{{\vec v \bullet \vec u}}{{\vec u \bullet \vec u}}\vec u\]
\[{p_{/\vec u}}\left( {\vec v} \right)\] est colinéaire à \[\vec u\] et \[\vec v - {p_{/\vec u}}\left( {\vec v} \right)\] lui est orthogonal.
Remarque
Le coefficient \[\frac{{\vec * \bullet \vec u}}{{\vec u \bullet \vec u}}\] est appelé coefficient de Fourier de \[\vec v\] sur \[\vec u\] ou composante de \[\vec v\] sur \[\vec u\].
Définition 2
Soit \[\vec u \in {\mathbb{R}^n}\]. L’application \[{p_{/\vec u}}\] de \[{\mathbb{R}^n}\]* *dans \[{\mathbb{R}^n}\] qui à \[\vec v\] associe \[{p_{/\vec u}}\left( {\vec v} \right)\] est appelé projecteur orthogonal sur \[\vec u\].
è Revoir la notion de projecteur](http://biogeol.free.fr/Lexique/Lexique.htm).
4 Distance euclidienne
Définition
Soient \[\vec u = \left( {{u_1}, \ldots ,{u_n}} \right)\] et \[\vec v = \left( {{v_1}, \ldots ,{v_n}} \right)\] deux vecteurs de \[{\mathbb{R}^n}\]. La distance entre \[\vec u\] et \[\vec v\], qui n’est autre que la distance entre les points extrémités des deux vecteurs, est définie par :
\[d\left( {\vec u,\vec v} \right) = \left\| {\vec u - \vec v} \right\|\]
Proposition
Soit \[{\mathbb{R}^n}\] espace euclidien. Alors : * \[d\left( {\vec u,\vec v} \right) = \left\| {\vec u - \vec v} \right\| = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{u_i} - {v_i}} \right)}^2}} } \]
On parle de distance euclidienne.
Exemple
On se place dans \[{\mathbb{R}^2}\] muni de sa base canonique \(\left\{ {{{\vec e}_1},{{\vec e}_2}} \right\}\) et de son produit scalaire canonique.
Soit \(\vec u = \;\left( {1,3} \right)\) et \(\vec v = \;\left( { * 1,2} \right)\). Calculer \(d\left( {\vec u,\vec v} \right)\). Réponse.
5 Déterminant et volume
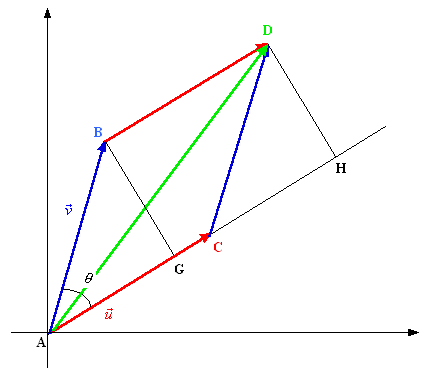
Considérons le plan muni d’un repère d’origine A. On considère \[{\mathbb{R}^2}\] espace euclidien.
Soient \(A\) de cordonnées \[\left( {0,0} \right)\], \(B\) de coordonnées \[\left( {{x_1},{x_2}} \right)\], \(C\) de coordonnées \[\left( {{y_1},{y_2}} \right)\]. On désigne par \[\vec u\] le vecteur issu de \(A\) et d’extrémité \(C\) et par \[\vec v\] le vecteur issu de \(A\) et d’extrémité \(B\). Ainsi, \[\vec u = \left( {{x_1},{x_2}} \right)\] et \[\vec v = \left( {{y_1},{y_2}} \right)\]. On appelle \[\theta \] l’angle formé par \[\vec u\] et \[\vec v\].
Nous allons cherche à démontrer la propriété énoncée au chapitre 3, paragraphe 4.4, à savoir que le déterminant de \[\vec u\] et \[\vec v\] est égal à l’aire du parallélogramme ABDC.
On appelle respectivement G et H les projetés orthogonaux de * et D sur la direction définie par \[\vec u\]. Ainsi, l’aire du triangle ABG est égale à l’aire du triangle CDH, d’où l’on en déduit que l’aire du parallélogramme ABDC est exactement égale à l’aire du rectangle GBDH :
\[{A_{ABDC}} = {A_{GBDH}}\]
Or \[{A_{GBDH}} = BD \times BG\] avec \[BD = AC = \left\| {\vec u} \right\|\] et \[BG = AB\sin \theta = \left\| {\vec v} \right\|\sin \theta \]. Donc :
\(\begin{gathered}\)
{A_{ABDC}} = | {u} || {v} |\$
= | {u} || {v} | \$
= \$
= \$
$\end{gathered} $
En utilisant les coordonnées des vecteurs \[\vec u\] et \[\vec v\], on peut écrire :
\({\left\| {\vec u} \right\|^2} = x_1^2 + x_2^2\) \({\left\| {\vec v} \right\|^2} = y_1^2 + y_2^2\) \[\vec u \bullet \vec v = {x_1}{y_1} + {x_2}{y_2}\]
Finalement :
\(\begin{gathered}\)
{A_{ABDC}} = \$
= \$
= \$
= \$
= {x_1}{y_2} - {x_2}{y_1} \$
$\end{gathered} $
En remarquant que \[\det \left( {\vec u,\vec v} \right) = {x_1}{y_2} - {x_2}{y_1}\], on peut conclure que \(\boxed{{A_{ABDC}} = \det \left( {\vec u,\vec v} \right)}\), autrement dit que le déterminant de deux vecteurs de \[{\mathbb{R}^2}\] est bien égal à la surface du parallélogramme construit sur ces deux vecteurs.
6 Exemples d’utilisation en Biologie
Les plantes de quatre espèces végétales E1, E2, E3, E4ont été dénombrées sur un terrain subdivisé en trois parcelles disjointes A, B, C. Les résultats sont présentés sous la forme d’une matrice F :
\({\mathbf{F}} = \left( {\begin{array}{*{20}{c}}\)
{{a_1}}&{{a_2}}&{{a_3}}&{{a_4}} \$
{{b_1}}&{{b_2}}&{{b_3}}&{{b_4}} \$
{{c_1}}&{{c_2}}&{{c_3}}&{{c_4}}$
\(\end{array}} \right)\)
où, par exemple, \[{b_2}\] est le nombre de plantes de l’espèce E2présentes dans la parcelle B.
Soient \[{p_1},{p_2},{p_3},{p_4}\] les sommes des colonnes de la matrice \(F\) ; \[{n_1},{n_2},{n_3}\] les sommes des lignes de la matrice F : \[{p_i} = {a_i} + {b_i} + {c_i}\quad i = 1,4\] et \[{n_j} = \sum\limits_{i = 1}^{i = 4} {{a_i}} \quad j = 1,3\].
Ainsi \[{n_2}\] est le nombre total de plantes présentes dans la parcelle B ; tandis que \[{p_2}\] est le nombre total de plantes de l’espèce E2présentes dans l’ensemble des trois parcelles.
Soit \(n\) le nombre total de plantes des quatre espèces présentes dans l’ensemble des trois parcelles : \[n = \sum\limits_{i = 1}^{i = 4} {{p_i}} = \sum\limits_{j = 1}^{j = 3} {{n_j}} \].
Considérons les deux matrices suivantes :
\(${\mathbf{D}} = \left( {\begin{array}{*{20}{c}}\)
{{p_1}}&0&0&0 \$
0&{{p_2}}&0&0 \$
0&0&{{p_3}}&0 \$
0&0&0&{{p_4}}$
\(\end{array}} \right)\)$ \({\mathbf{\Delta }} = \left( {\begin{array}{*{20}{c}}\)
- {{{{n_1}} \mathord{/$
\({\vphantom {{{n_1}} n}} \right.\)
\($\kern-\nulldelimiterspace} n}}&0&0 \\\)
- 0&{{{{n_2}} \mathord{/$
\({\vphantom {{{n_2}} n}} \right.\)
\(\kern-\nulldelimiterspace} n}}&0 \\\)
- 0&0&{{{{n_3}} \mathord{/$
\({\vphantom {{{n_3}} n}} \right.\)
\(\kern-\nulldelimiterspace} n}}\)
\(\end{array}} \right)\)
Dans \[{\mathbb{R}^3}\] (muni de sa base canonique), les colonnes de la matrice \({\mathbf{X}} = {\mathbf{F}}{{\mathbf{D}}^{ - 1}}\) peuvent être considérées comme les coordonnées, exprimées en %, des quatre points E1, E2, E3, E4représentants les quatre espèces végétales :
\({\mathbf{X}} = {\mathbf{F}}{{\mathbf{D}}^{ - 1}} = \left( {\begin{array}{*{20}{c}}\)
{{a_1}}&{{a_2}}&{{a_3}}&{{a_4}} \$
{{b_1}}&{{b_2}}&{{b_3}}&{{b_4}} \$
{{c_1}}&{{c_2}}&{{c_3}}&{{c_4}}$
\(\end{array}} \right)\left( {\begin{array}{*{20}{c}}\)
- {{1 \mathord{/$
\({\vphantom {1 {{p_1}}}} \right.\)
\($\kern-\nulldelimiterspace} {{p_1}}}}&0&0&0 \\\)
- 0&{{1 \mathord{/$
\({\vphantom {1 {{p_2}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_2}}}}&0&0 \\\)
- 0&0&{{1 \mathord{/$
\({\vphantom {1 {{p_3}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_3}}}}&0 \\\)
- 0&0&0&{{1 \mathord{/$
\({\vphantom {1 {{p_4}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_4}}}}\)
\(\end{array}} \right) = \left( {\begin{array}{*{20}{c}}\)
- {{{{a_1}} \mathord{/$
\({\vphantom {{{a_1}} {{p_1}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_1}}}}&{{{{a_2}} \mathord{\left/\)
\({\vphantom {{{a_2}} {{p_2}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_2}}}}&{{{{a_3}} \mathord{\left/\)
\({\vphantom {{{a_3}} {{p_3}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_3}}}}&{{{{a_4}} \mathord{\left/\)
\({\vphantom {{{a_4}} {{p_4}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_4}}}} \\\)
- {{{{b_1}} \mathord{/$
\({\vphantom {{{b_1}} {{p_1}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_1}}}}&{{{{b_2}} \mathord{\left/\)
\({\vphantom {{{b_2}} {{p_2}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_2}}}}&{{{{b_3}} \mathord{\left/\)
\({\vphantom {{{b_3}} {{p_3}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_3}}}}&{{{{b_4}} \mathord{\left/\)
\({\vphantom {{{b_4}} {{p_4}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_4}}}} \\\)
- {{{{c_1}} \mathord{/$
\({\vphantom {{{c_1}} {{p_1}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_1}}}}&{{{{c_2}} \mathord{\left/\)
\({\vphantom {{{c_2}} {{p_2}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_2}}}}&{{{{c_3}} \mathord{\left/\)
\({\vphantom {{{c_3}} {{p_3}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_3}}}}&{{{{c_4}} \mathord{\left/\)
\({\vphantom {{{c_4}} {{p_4}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_4}}}}\)
\(\end{array}} \right)\)
Par cette opération matricielle, on a en fait normalisé les colonnes de \(F\) (\[{p_i} = {a_i} + {b_i} + {c_i}\]).
Nous allons tenter de voir si les quatre espèces végétales sont équi-réparties au sein des trois parcelles, i.e. si les proportions des quatre espèces sont les mêmes quelle que soit la parcelle.
Si on appelle G le point de coordonnées \[\left( {\frac{{{n_1}}}{n},\frac{{{n_2}}}{n},\frac{{{n_3}}}{n}} \right)\], cela revient d’un point de vue géométrique, à situer les quatre point E1, E2, E3, E4par rapport à ce point G. G représente le barycentre des espèces. Si un point Eiest proche de G, alors on pourra dire que cette espèce est équi-répartie au sein des trois parcelles.
D’un point de vue mathématique, il faut calculer les distances \[d\left( {{\text{G}}{\text{,}}{{\text{E}}_{\text{i}}}} \right)\], les distances les plus petites correspondront aux espèces les mieux équi-réparties au sein des trois parcelles.
\(${{\text{E}}_{\text{i}}} = \left( {\begin{array}{*{20}{c}}\)
- {{{{a_i}} \mathord{/$
\({\vphantom {{{a_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}}} \\\)
- {{{{b_i}} \mathord{/$
\({\vphantom {{{b_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}}} \\\)
- {{{{c_i}} \mathord{/$
\({\vphantom {{{c_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}}}\)
\(\end{array}} \right)\)$ \[i = 1,4\] \[d\left( {{\text{G}}{\text{,}}{{\text{E}}_{\text{i}}}} \right) = \left\| {\overrightarrow {{\text{G}}{{\text{E}}_{\text{i}}}} } \right\|\] \($\overrightarrow {{\text{G}}{{\text{E}}_{\text{i}}}} * \left( {\begin{array}{*{20}{c}}\)
- {{{{a_i}} \mathord{/$
\({\vphantom {{{a_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}} - {{{n_1}} \mathord{\left/\)
\({\vphantom {{{n_1}} n}} \right.\)
\(\kern-\nulldelimiterspace} n}} \\\)
- {{{{b_i}} \mathord{/$
\({\vphantom {{{b_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}} - {{{n_2}} \mathord{\left/\)
\({\vphantom {{{n_2}} n}} \right.\)
\(\kern-\nulldelimiterspace} n}} \\\)
- {{{{c_i}} \mathord{/$
\({\vphantom {{{c_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}} - {{{n_3}} \mathord{\left/\)
\({\vphantom {{{n_3}} n}} \right.\)
\(\kern-\nulldelimiterspace} n}}\)
\(\end{array}} \right)\)$
Ainsi, \($d\left( {{\text{G}}{\text{,}}{{\text{E}}_{\text{i}}}} \right) = \left\| {\overrightarrow {{\text{G}}{{\text{E}}_{\text{i}}}} } \right\| = \sqrt {{{\left( {{{{a_i}} \mathord{\left/\)
\({\vphantom {{{a_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}} - {{{n_1}} \mathord{\left/\)
\({\vphantom {{{n_1}} n}} \right.\)
\(\kern-\nulldelimiterspace} n}} \right)}^2} + {{\left( {{{{b_i}} \mathord{\left/\)
\({\vphantom {{{b_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}} - {{{n_2}} \mathord{\left/\)
\({\vphantom {{{n_2}} n}} \right.\)
\(\kern-\nulldelimiterspace} n}} \right)}^2} + {{\left( {{{{c_i}} \mathord{\left/\)
\({\vphantom {{{c_i}} {{p_i}}}} \right.\)
\(\kern-\nulldelimiterspace} {{p_i}}} - {{{n_3}} \mathord{\left/\)
\({\vphantom {{{n_3}} n}} \right.\)
$-} n}} )}^2}} $$.
Application numérique : considérons la matrice \(F\) suivante :
\({\mathbf{F}} = \left( {\begin{array}{*{20}{c}}\)
6&7&{17}&2 \$
{15}&{22}&2&{14} \$
3&4&6&2$
\(\end{array}} \right)\)
\[{p_1} = 24,{p_2} = 33,{p_3} * 25,{p_4} = 18\] \[{n_1} = 32,{n_2} = 53,{n_3} = 15\] \[n = 100\]
\({\mathbf{X}} = \left( {\begin{array}{*{20}{c}}\)
{0.250}&{0.212}&{0.680}&{0.111} \$
{0.625}&{0.666}&{0.08}&{0.777} \$
{0.125}&{0.121}&{0.240}&{0.111}$
\(\end{array}} \right)\) avec \(${\text{G}} = \left( {\begin{array}{*{20}{c}}\)
{0.32} \$
{0.53} \$
{0.15}$
\(\end{array}} \right)\)$
Ainsi \($\overrightarrow {{\text{G}}{{\text{E}}_{\text{1}}}} = \left( {\begin{array}{*{20}{r}}\)
{ - 0.070} \$
{0.095} \$
{ - 0.025}$
\(\end{array}} \right)\)$, \($\overrightarrow {{\text{G}}{{\text{E}}_{\text{2}}}} = \left( {\begin{array}{*{20}{r}}\)
{ - 0.108} \$
{0.136} \$
{ - 0.029}$
\(\end{array}} \right)\)$, \($\overrightarrow {{\text{G}}{{\text{E}}_{\text{3}}}} = \left( {\begin{array}{*{20}{r}}\)
{0.36} \$
{ - 0.45} \$
{0.09}$
\(\end{array}} \right)\)$ et \($\overrightarrow {{\text{G}}{{\text{E}}_{\text{4}}}} = \left( {\begin{array}{*{20}{r}}\)
{ - 0.209} \$
{0.247} \$
{ - 0.039}$
\(\end{array}} \right)\)$.
Alors \[\left\| {\overrightarrow {{\text{G}}{{\text{E}}_{\text{1}}}} } \right\| = 0.120\], \[\left\| {\overrightarrow {{\text{G}}{{\text{E}}_{\text{2}}}} } \right\| = 0.176\], \[\left\| {\overrightarrow {{\text{G}}{{\text{E}}_{\text{3}}}} } \right\| = 0.583\] et \[\left\| {\overrightarrow {{\text{G}}{{\text{E}}_{\text{4}}}} } \right\| = 0.326\].
Nous pouvons finalement conclure que, dans cet exemple numérique, c’est l’espère 1 qui la mieux équi-répartie au sein des trois parcelles.