Chapitre 6 — Estimation

2.1.1 Approche empirique

Il est possible d’extraire d’une population de paramètres \(p\), \(\mu\) ou ^2$ pour une variable aléatoire \(X\), \(k\) échantillons aléatoires simples de même effectif, \(n\). Sur chaque échantillon de taille \(n\), on calcule les paramètres descriptifs (\(f\), \(\bar{x}\), \(s^2\)).

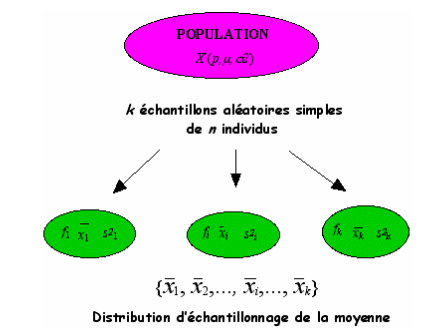
On obtient ainsi pour chaque paramètre estimé, une série statistique composée de \(k\) éléments à savoir les \(k\) estimations du paramètre étudié. Par exemple, on aura \(k\) valeurs de moyennes observées (graphe ci-dessus).

La distribution associée à ces \(k\) estimations constitue la distribution d’échantillonnage du paramètre. On peut alors associer une variable aléatoire à chacun des paramètres. La loi de probabilité suivie par cette variable aléatoire admet comme distribution, la distribution d’échantillonnage du paramètre auquel on pourra associer une espérance et une variance.

2.1.2 Approche théorique

En pratique, les données étudiées sont relatives à un seul échantillon. C’est pourquoi, il faut rechercher les propriétés des échantillons susceptibles d’être prélevés de la population ou plus précisément les lois de probabilité de variables aléatoires associées à un échantillon aléatoire.

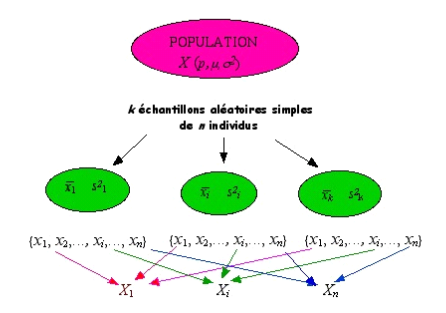
Ainsi les \(n\) observations \(x_1 , x_2 ,..., x_i , ..., x_n\), faites sur un échantillon peuvent être considérées comme \(n\) variables aléatoires \(X_1 , X_2 ,..., X_i , ..., X_n\). En effet, la valeur prise par le premier élément extrait de la population \(X_1\), dépend de l’échantillon obtenu lors du tirage aléatoire. Cette valeur sera différente si l’on considère un autre échantillon. Il en est de même pour les \(n\) valeurs extraites de la population.

A partir de ces \(n\) variables aléatoires, on peut définir alors une nouvelle variable qui sera fonction de ces dernières telle que :

\(Y = f(X_1 , X_2 ,..., X_i , ..., X_n)\)

par exemple : \(Y = X_1 + X_2 +...+ X_i + ...+ X_n\)

Ainsi la loi de probabilité de la variable aléatoire \(Y\) dépendra à la fois de la loi de probabilité de la variable aléatoire \(X\) et de la nature de la fonction \(f\).

2.2.1 Définition

Soit \(X\) une variable aléatoire suivant une loi normale d’espérance \(\mu\) et de variance \(\sigma^2\) et \(n\) copies indépendantes \(X_1 , X_2 ,..., X_i , ..., X_n\) telle que \(X_i\) associe le i^ème élément de chacun des \(n\) échantillons avec \(E(X_i) = \mu\) et \(V(X)=\sigma^2\)

On construit alors la variable aléatoire \(\bar{X}\), telle que

\(\bar{X}= \frac{{X_1} + {X_2} + ... + {X_i} + ... + {X_n}}{n} = \frac{1}{n}\sum\limits_{i = 1}^n {{X_i}}\)

avec pour espérance :

\(E(\bar{X)}= E(\frac{1}{n}\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{n}E(\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{n}\sum\limits_{i = 1}^n {E({X_i}} ) = \frac{1}{n}n\mu\)

d’où \(E(\bar{X)}= \mu\) \(\qquad E(\bar{X)}\) est notée également \({\mu_{\bar{X}}}\)

et pour variance si \(V(X_i) = \sigma^2\) :

\(V(\bar{X)}= V(\frac{1}{n}\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{{{n^2}}}V(\sum\limits_{i = 1}^n {{X_i}} ) = \frac{1}{{{n^2}}}\sum\limits_{i = 1}^n {V({X_i}} ) = \frac{1}{{{n^2}}}n{\sigma ^2}\)

d’où \(V(\bar{X)}= \frac{{{\sigma ^2}}}{n}\) \(\qquad V(\bar{X)}\) est notée également \(\sigma_{\bar{X}^2}\)

Remarque : il est aisé de voir sur le graphe ci-dessous que la variance associée à une moyenne (\(\frac{\sigma ^2}{n}\)) est plus faible que la variance de la variable elle-même (\(\sigma^2\)).

Soit l’étendue des valeurs observées d’une variable aléatoire \(X\) pour 4 échantillons de même taille d’une même population.

Les valeurs des moyennes arithmétiques sont indiquées ainsi que les limites relatives à l’étendue des valeurs de la variable observée et celle des moyennes observées.

Exemple :

Des études statistiques montrent que le taux de glucose dans le sang est une variable normale \(X\) d’espérance \(\mu = 1\) g/l et d’écart-type \(\sigma = 0,1\) g/l.

En prenant un échantillon de 9 individus dans la population, l’espérance et l’écart-type théorique attendu de la variable aléatoire \(\bar{X}\) sont alors :

\({\mu_{\bar{X}}} = \mu = 1\) g/l et \(\sigma_{\bar{X}} = \frac{\sigma }{\sqrt n} = \frac{0,1}{\sqrt 9} =\) 0,03 g/l

2.2.2 Convergence

En fonction de la nature de la variable aléatoire continue \(X\), de la taille de l’échantillon \(n\) et de la connaissance que nous avons sur le paramètre \(\sigma^2\), la variable centrée réduite construite avec \(\bar{X}\) converge vers différentes lois de probabilité (Table de convergence).

3.2.1 Convergence

Ceci équivaut à dire qu’en limite \(\Theta \to \theta\) lorsque \(n \to \infty\).

3.2.2 Biais d’un estimateur

Le biais d’un estimateur noté \(B(\Theta)\) est la différence moyenne entre sa valeur et celle du paramètre qu’il estime. Le biais doit être égal à 0 pour avoir un bon estimateur.

\(B(\Theta) = E(\Theta - \theta) = E(\Theta) - E(\theta) = E(\Theta) - \theta = 0\) (voir propriétés de l’espérance)

d’où \(E(\Theta) = \theta\)

Exemple :

Soit les densités de probabilité de 3 estimateurs d’une espérance \(\mu\),

Dans l’exemple ci-dessus, \(\Theta_1\) et \(\Theta_2\) sont des estimateurs sans biais de \(\mu\) car \(B(\Theta_1) = E(\Theta_1- \mu) = E(\Theta_1) - \mu = 0\) car \(E(\Theta_1) - \mu\), de même pour \(B(\Theta_2)\)

alors que \(\Theta_3\) est un estimateur biaisé de \(\mu\) car

\(B(\Theta_3) = E(\Theta_3 - \mu) = E(\Theta_3) - \mu = \mu' - \mu \neq 0\) car \(E(\Theta_3) = \mu'\)

Remarque: Un estimateur est asymptotiquement sans biais si \(E(\Theta) \to \theta\) lorsque \(n \to \infty\).

3.2.3 Variance d’un estimateur

Exemple :

Dans l’exemple précédent, on voit que \(V(\Theta_1) < V(\Theta_2)\). On peut donc conclure que \(\Theta_1\) est un meilleur estimateur de \(\mu\) que \(\Theta_2\).

Remarque : Quand les estimateurs sont biaisés, en revanche, leur comparaison n’est pas simple. Ainsi un estimateur peu biaisé mais de variance très faible, pourrait même être préféré à un estimateur sans biais mais de grande variance.

Cette inégalité exprime que si \(|\Theta - \theta|\) tend vers 0 quand \(n\) augmente, \(V(\Theta)\) doit aussi tendre vers 0.

4.1.1. Espérance

Soit \(X\) une variable aléatoire continue suivant une loi normale \(\mathcal{N}(\mu,\sigma)\) dont la valeur des paramètres n’est pas connue et pour laquelle on souhaite estimer l’espérance \(\mu\).

Soient \({X_1},{X_2},...,{X_i},...,{X_n}\), \(n\) réalisations indépendantes de la variable aléatoire \(X\), un estimateur du paramètre \(\mu\) est une suite de variable aléatoire \(\Theta\) fonctions des \(X_i\) :

\(\Theta = f(X_1,X_2,...,X_i,...,X_n)\)

La méthode des moindres carrés consiste à rechercher les coefficients de la combinaison linéaire

\(\Theta = {a_1}{X_1} + {a_2}{X_2} + ... + {a_i}{X_i} + ... + {a_n}{X_n}\)

telle que \(E(\Theta)= \mu\) et \(V(\Theta)\) soit minimale (voir démonstration)

Voici pourquoi :

Estimateur sans biais : \(E(\bar{X}) = \mu\) (voir loi de la moyenne)

Estimateur convergent : si l’on pose l’inégalité de Biénaymé-Tchébycheff :

\(P( | \bar{X} - \mu | \geq \varepsilon) \leq \frac{V(\bar X)}{\varepsilon^2}\) avec \(\varepsilon > 0\)

lorsque \(n \to \infty \qquad \frac{V(\bar{X})}{\varepsilon^2}= \frac{\sigma^2}{n \varepsilon^2}\) et ceci ainsi en limite, \(P( | \bar{X} - \mu | \geq \varepsilon ) = 0\) ce qui indique que \(\bar{X} \to \mu\) en probabilité.

4.1.2. Variance

Soit \(X\) une variable aléatoire continue suivant une loi normale \(\mathcal{N}(\mu,\sigma)\) pour laquelle on souhaite estimer la variance \(\sigma^2\).

Soient \(X_1,X_2,...,X_i,...,X_n\) réalisations indépendantes de la variable aléatoire \(X\), un estimateur du paramètre \(\sigma^2\) est une suite de variable aléatoire \(\Theta\) fonctions des \(X_i\):

\(\Theta = f({X_1} + {X_2} + ... + {X_i} + ... + {X_n})\)

• Cas où l’espérance \(\mu\) est connue

La méthode des moindres carrés consiste à rechercher les coefficients de la combinaison linéaire

\(\Theta = a_1(X_1 - \mu )^2 + a_2(X_2 - \mu )^2 + ... + a_i(X_i - \mu )^2 + ... + a_n(X_n - \mu )^2\)

telle que \(E(\Theta) = \sigma^2\) et \(V(\Theta)\) soit minimale (voir démonstration)

Remarque : Cette estimation de la variance de la population est rarement utilisée dans la mesure où si la variance \(\sigma^2\) n’est pas connue, l’espérance \(\mu\) ne l’est pas non plus.

• Cas où l’espérance \(\mu\) est inconnue

Dans ce cas, nous allons estimer m avec \(\hat \mu = \bar{X}\) et dans ce cas \(\sum\limits_{i = 1}^n {{({X_i} - \mu )}^2} \ne \sum\limits_{i = 1}^n {({X_i}} - \bar{X{)^2}}\). Nous allons étudier la relation entre ces deux termes à partir de la variance observée :

\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \bar{X{)^2}}= \frac{1}{n}\sum\limits_{i = 1}^n {[({X_i}} - \mu ) - (\bar{X}- \mu ){]^2}\)

\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {[({X_i}} - \mu {)^2} + {(\bar{X}- \mu )^2} - 2({X_i} - \mu )(\bar{X}- \mu ){]^{}}\)

\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \mu {)^2} + \frac{1}{n}\sum\limits_{i = 1}^n {{{(\bar{X}- \mu )}^2}} - 2(\bar{X}- \mu ){\sum\limits_{i = 1}^n {({X_i} - \mu )} ^{}}\) avec \({\sum\limits_{i = 1}^n {({X_i} - \mu )} ^{}}\)= \(n(\bar{X}- \mu )\)

\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \mu {)^2} + {(\bar{X}- \mu )^2} - 2{(\bar{X}- \mu )^2}\)

\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({X_i}} - \mu {)^2} - {(\bar{X}- \mu )^2} = {\sigma ^2} - \frac{{{\sigma ^2}}}{n}\) en effet \(\sigma_{\bar{X}^2}= \frac{1}{n}\sum\limits_{i = 1}^n {(\bar{X}}- \mu {)^2} = {(\bar{X}- \mu )^2} = \frac{{{\sigma ^2}}}{n}\)

ainsi \({s^2} = \frac{{n - 1}}{n}{\sigma ^2}\)

Remarque : Lorsque \(n\) augmente, la variance observée \(s^2\) tend vers la variance de la population \(\sigma^2\).

\(\lim\limits_{n \to + \infty } s^2 = \lim\limits_{n \to + \infty } \frac{n-1}{n} \sigma^2 = \sigma^2\)

4.1.3. Fréquence

Soit le schéma de Bernoulli dans lequel le caractère A correspond au succés. On note \(p\) la fréquence des individus de la population possédant le caractère A. La valeur de ce paramètre étant inconnu, on cherche à estimer la fréquence \(p\) à partir des données observables sur un échantillon.

A chaque échantillon non exhaustif de taille \(n\), on associe l’entier \(k\), nombre d’individus possédant le caractère A.

Soit \(K\) une variable aléatoire discrète suivant une loi binomiale \(\mathcal{B}(n,p)\) et pour laquelle on souhaite estimer la fréquence \(p\).

Voici pourquoi :

Estimateur sans biais : \(E(\frac{K}{n}) = p\) (voir loi d’une fréquence)

Estimateur convergent : si l’on pose l’inégalité de Biénaymé-Tchébycheff :

\(P( | \frac{K}{n} - p | \geq \varepsilon ) \leq \frac{V(\frac{K}{n})}{\varepsilon ^2}\) avec \(\varepsilon > 0\)

alors lorsque \(n \to \infty \quad \frac{V(\frac{K}{n})}{\varepsilon ^2} = \frac{pq}{n{\varepsilon ^2}} \to 0\) et ceci \(\forall \varepsilon > 0\)

ainsi en limite \(P(| \frac{K}{n}- p| \geq \varepsilon ) = 0\) ce qui indique que \(\frac{K}{n} \to p\) en probabilité.

Remarque : Nous avions déjà avancé cette propriété lors de l’établissement de la loi des grands nombres.

Exemple :

On a prélevé au hasard, dans une population de lapin, 100 individus. Sur ces 100 lapins, 20 sont atteints par la myxomatose. Le pourcentage de lapins atteints par la myxomatose dans la population est donc : \(\hat{p} = \frac{K}{n} = \frac{20}{100}\) = 0,2 soit 20% de lapins atteins dans la population

Ce résultat n’aura de signification que s’il est associé à un interval de confiance.

4.2.1. Définition

L’estimation par intervalle associe à un échantillon aléatoire, un intervalle [\(\hat{\theta_1}\),\(\hat{\theta_2}\)] qui recouvre \(\theta\) avec une certaine probabilité.

Un intervalle de confiance indique la précision d’une estimation car pour un risque \(\alpha\) donné, l’intervalle est d’autant plus grand que la précision est faible comme l’indiquent les graphes ci-dessous. Pour chaque graphe, l’aire hachurée en vert correspond au coefficient de risque \(\alpha\). Ainsi de part et d’autre de la distribution, la valeur de l’aire hachurée vaut \(\frac{\alpha }{2}\).

4.2.2 Intervalle de confiance d’une moyenne

En fonction de la nature de la variable aléatoire continue \(X\), de la taille de l’échantillon \(n\) et de la connaissance que nous avons sur le paramètre \(\sigma^2\), l’établissement de l’intervalle de confiance autour de \(\mu\) sera différent.

• Quelque soit la valeur de \(n\), si \(X \to \mathcal{N} (\mu , \sigma )\) et \(\sigma^2\) est connue, établir l’intervalle de confiance autour de la moyenne \(\mu\) revient à établir la valeur de \(i\) pour une valeur du coefficient de confiance 1 - a donnée par l’expérimentateur.

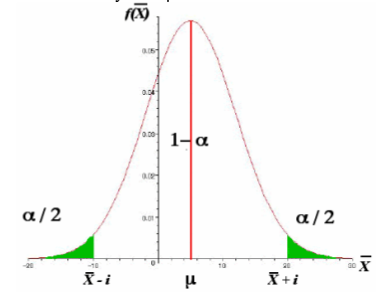
Voici comment :

Si \(P(\bar{X} - i < \mu < \bar{X}+ i ) = 1 - \alpha\) alors \(P(\mu - i < bar{X} < \mu + i ) = 1 - \alpha\)

Connaissant la loi suivie par la v.a. \(\bar{X}\) et d’après le théorème central limite, on peut établir que \(P(\frac{ - i}{\sigma / \sqrt {n} } < \frac{\bar{X}- \mu }{\sigma / \sqrt{n} } < \frac{ + i}{\sigma / \sqrt {n} }) = 1 - \alpha\) sachant que \(\frac{\bar{X}- \mu }{ \sigma /\sqrt {n} } \to \mathcal{N}(0,1)\) (conditions)

par conséquence \(\left| \frac{i}{\sigma / \sqrt{n} } \right|\) correspond à la valeur de la variable normale réduite pour probabilité \(\alpha\) donnée notée \(\varepsilon_{\alpha}\) ou écart réduit.

ainsi \(\left| \frac{i}{\sigma /\sqrt {n}} \right| = \varepsilon_{\alpha}\) implique \(i = \varepsilon_{\alpha} \times \frac{\sigma }{\sqrt {n} }\)

Exemple :

Pour des masses comprises entre 50g et 200g, une balance donne une pesée avec une variance de 0,0015. Les résultats des trois pesées d’un même corps sont : 64,32 ; 64,27 ; 64 ,39.

On veut connaître le poids moyen de ce corps dans la population avec un coefficient de confiance de 99%.

avec \(\bar{X}\)= 64,33 et \(\varepsilon_{\alpha}\)= 2,576 alors \(\varepsilon_{\alpha} \frac{\sigma}{\sqrt {n} } = 2,576 \times \frac{0,039}{1,732}\)= 0,058

et donc \(\mu = \bar{X} \pm \varepsilon_{\alpha} \frac{\sigma }{\sqrt n}\) = 64,33g ± 0,058

d’où le poids moyen de ce corps est compris dans l’intervalle [64,27 ; 64,39] avec une probabilité de 0,99.

Remarque : La valeur de \(\varepsilon_{\alpha}\) est donnée par la table de l’écart-réduit pour une valeur \(\alpha\) donnée.

• Quelque soit la valeur de \(n\), si \(X \to (\mu , \sigma )\) et \(\sigma^2\) est inconnue

Le raisonnement reste le même mais la variance de la population \(\sigma^2\) doit être estimée par

\(\hat{\sigma ^2} = \frac{n}{n - 1} s^2\) (voir estimation ponctuelle)

Si \(P( \bar{X} - i < \mu < \bar{X} + i ) = 1 - \alpha\) alors \(P(\mu - i < bar{X} < \mu + i ) = 1 - \alpha\)

Connaissant la loi suivie par la v.a. \(\bar{X}\) et celle suivie par la variable centrée réduite, on peut établir que \(P\left( \frac{ - i}{ \hat {\sigma} / \sqrt{n} } < \frac{ \bar{X} - \mu }{ \hat{\sigma} / \sqrt {n} } < \frac{ +i}{\hat{\sigma} / \sqrt {n} } \right) = 1 - \alpha\) sachant que \(\frac{\bar{X}- \mu}{\hat{\sigma} / \sqrt{n} } \to T(n-1 \ \text{d.d.l.})\) (conditions)

par conséquence \(\left| \frac{i}{\hat{\sigma} / \sqrt {n} } \right|\) correspond à la valeur de la variable de student pour une valeur de probabilité a donnée notée \(t_{\alpha}\) pour \(n - 1\) degrés de liberté.

Ainsi \(\left| \frac{i}{ \hat{\sigma} / \sqrt{n} } \right| = t_{\alpha}\) implique \(i = t_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}}\)

Remarque : Lorsque \(n > 30\) la loi de student converge vers une loi normale réduite ainsi la valeur de \(t_{\alpha}(n-1)\) est égale à \(\varepsilon_{\alpha}\). Ci-dessous, un exemple pour un risque \(\alpha = 0,05\)

Exemples :

1. Dans un échantillon de 20 étudiants de même classe d’âge et de même sexe, la taille moyenne observée est de 1,73m et l’écart-type de 10 cm. La taille moyenne de l’ensemble des étudiants de l’université est donc :

avec \(\bar{x} =\) 1,73m ; \(\hat{\sigma^2} = \frac{n}{n - 1} s^2 = \frac{20}{19} \times 0,01=\) 0,011 et \(t_{\alpha} =\) 2,086

d’où \(t_{\alpha} \frac{\hat {\sigma}}{\sqrt {n} } = 2,086 \times \sqrt {\frac{0,011}{20}} =\) 0,049 ainsi \(\mu = \bar{X} \pm t_{\alpha} \frac{\hat{\sigma} }{ \sqrt {n}} =\) 1,73 ± 0,049

La taille moyenne des étudiants dans la population est comprise dans l’intervalle [1,68 ; 1,78] avec une probabilité de 0,95.

2. Dans un échantillon de 100 étudiants, la taille moyenne de la population est :

\(\bar{x} =\) 1,73m ; \({\hat \sigma ^2} = \frac{n}{n - 1} s^2 = \frac{100}{99} \times 0,01=\) 0,01 et \(\varepsilon_{\alpha}=\) 1,960

d’où \(\varepsilon_{\alpha} \frac{{\hat \sigma }}{{\sqrt n }} = 1,960 \times \sqrt {\frac{{0,010}}{{100}}} =\) 0,02 ainsi \(\mu = \bar{X}\pm {\varepsilon_\alpha }\frac{{\hat \sigma }}{{\sqrt n }}\) = 1,73 ± 0,02

La taille moyenne des étudiants dans la population est comprise dans l’intervalle [1,71 ; 1,75] avec une probabilité de 0,95.

Ainsi lorsque la taille de l’échantillon augmente pour un même coefficient de confiance \((1- \alpha)\) , l’estimation autour de m est plus précise.

• Si \(n > 30\) et \(X\) suit une loi inconnue

La démarche est la même que pour le cas précédent puisque par définition la variance de la population est inconnue et doit être estimée avec la variance observée :

\({\hat \sigma ^2} = \frac{n}{{n - 1}}{s^2}\) (voir estimation ponctuelle)

Comme pour le cas 1, la loi suivie par la variable centrée réduite \(\frac{{\bar{X}- \mu }}{{\hat \sigma /\sqrt n }} \to \mathcal{N}(0,1)\) (conditions).

• Si \(n < 30\) et \(X\) suit une loi inconnue,

La loi de probabilité suivie par \(\frac{\bar{X}- \mu}{\hat{\sigma} / \sqrt {n} }\) n’est pas connue et l’on a recours aux statistiques non paramétriques.

4.2.3 Intervalle de confiance d’une proportion

Etablir l’intervalle de confiance autour de la fréquence \(p\) de la population à partir de son estimateur \(\frac{K}{n}\) revient à établir la valeur de \(i\) pour une valeur du coefficient de confiance \((1 - \alpha)\) donnée par l’expérimentateur telle que :

\(P(\frac{K}{n} - i < p < \frac{K}{n} + i ) = 1 - \alpha\) ou \(P(p - i < \frac{K}{n} < p + i ) = 1 - \alpha\)

Connaissant la loi suivie par la v.a. \(\frac{K}{n}\) et d’après le théorème central limite, on peut établir que \(P(\frac{ - i}{\sqrt {\frac{pq}{n}}} < \frac{\frac{K}{n} - p}{\sqrt {\frac{pq}{n}}} < \frac{ + i}{\sqrt {\frac{pq}{n}} }) = 1 - \alpha\) sachant que \(\frac{\frac{K}{n} - p}{\sqrt {\frac{pq}{n}} } \to \mathcal{N}(0,1)\)

par conséquence \(\left| {\frac{i}{\sqrt {\frac{pq}{n}} }} \right|\) correspond à la valeur de la variable normale réduite pour probabilité a donnée notée \(\varepsilon_{\alpha}\) ou écart réduit.

ainsi \(\left| {\frac{i}{\sqrt{\frac{pq}{n}}}} \right| = \varepsilon_{\alpha}\) implique \(i = \varepsilon_{\alpha} \times \sqrt{\frac{pq}{n}}\)

Par définition, \(V(\frac{K}{n})= \frac{pq}{n}\) n’est pas connue et on l’estime par \(\frac{\hat p \hat q}{n}\) avec \(\hat p = \frac{K}{n}\) et \(\hat q = \frac{n - K}{n}\)

Remarque : Si la taille de l’échantillon est faible, on a recours aux lois exactes.

Exemple :

Un laboratoire d’agronomie a effectué une étude sur le maintien du pouvoir germinatif des graines de Papivorus subquaticus après une conservaion de 3 ans.

Sur un lot de 80 graines, 47 ont germé. Ainsi la probabilité de germination des graines de Papivorus subquaticus après trois ans de conservation avec un coefficient de confiance de 95% est donc :

avec \(\hat p = \frac{K}{n} = \frac{47}{80} = 0,588\) , \(\hat q = \frac{n - K}{n} = \frac{33}{80} = 0,412\) et \(\varepsilon_\alpha= 1,96\)

alors \({\varepsilon_\alpha }\sqrt {\frac{{\hat p\hat q}}{n}} = 1,96 \times \sqrt {\frac{0,588 \times 0,412}{80}} = 0,108\) d’où \(p =\) 0,588 ± 0,108

ainsi la probabilité de germination est comprise dans l’intervalle [0,480 et 0,696] avec une probabilité de 0,95.