Introduction

(http://handy.univ-lyon1.fr/service/cours/info_deug/deug.int/semestr.1/equadiff/equa.html)

La notion d’équation différentielle apparaît chez les mathématiciens à la fin du XVIIème siècle. Encouragé par Huygens à étudier les mathématiques, Leibniz sera l’inventeur en 1686, en même temps que Newton, du calcul différentiel et intégral (Nova methodus pro maximis et minimis, 1684-86).

· A cette époque, les équations différentielles s’introduisent en mathématique par le biais de problèmes d’origine mécanique ou géométrique, comme par exemple :

· Vers 1700, beaucoup de ces problèmes étaient déjà partiellement ou totalement résolus et quelques méthodes de résolution mises au point. Ensuite, les mathématiciens se sont progressivement intéressés à des classes de plus en plus larges d’équations différentielles. Assez curieusement, les équations différentielles linéaires à coefficients constants sans second membre, qui apparaissent maintenant comme les plus simples, ne furent résolues qu’en 1739 par Euler. Il ne faut pas oublier que, pour les mathématiciens de cette époque, le maniement de la fonction exponentielle n’était pas encore familier.

â Dans la phase que nous venons de décrire, les mathématiciens s’attachent au calcul effectif d’une solution, à l’aide de ce que nous appelons maintenant les fonctions élémentaires, ce que nous allons faire dans ce chapitre 6.

· Vers 1870 Fuchs, puis Poincaré, vont inaugurer un nouveau champ de recherche. Le calcul effectif des solutions est la plupart du temps impossible, mais on peut chercher à déduire de l’examen a priori de l’équation les propriétés des solutions.

· Enfin, le développement moderne des moyens de calcul ajoute à cette panoplie la possibilité de calculer numériquement, dans un temps raisonnable, des solutions approchées très précises d’équations différentielles ou d’explorer les propriétés que l’on peut attendre des solutions.

â Dès le début du XXième siècle, les équations différentielles ont trouvé de nombreuses applications dans les Sciences de la Vie, lorsqu’est apparue la nécessité de relier le sujet biologique réel et la représentation qu’on en donne à travers un objet mathématique, que l’on appelle un modèle mathématique. Par exemple en démographie, les équations différentielles sont utilisées pour décrire l’évolution de la taille de la population d’un pays qui présente les caractéristiques suivantes : par an, le taux de renouvellement est de 20 pour 1000 habitants, et le taux de mortalité est de 15 pour 1000 habitants. Nous reviendrons sur la formalisation mathématique de ce problème à la fin du paragraphe 2.

1 Généralités

Définition 1 :

On appelle équation différentielle une relation entre les valeurs de la variable \(x\) et les valeurs \(y,y',y'', \ldots ,{y^{\left( n \right)}}\) d’une fonction inconnue et de ses dérivées au point \(x\).

On rappelle que :

On dit que l’équation différentielle est d’ordre \(n\) si elle contient la dérivée \(n\)-ième de \(y\), et pas celles d’ordre supérieur :

Définition 2 :

Une solution d’une équation différentielle est une fonction \(f\) continue et dérivable (jusqu’à l’ordre \(n\) pour une équation d’ordre \(n\)) dans un intervalle \(I\) donné, et telle que pour toute valeur \(x\) de \(I\), les valeurs de \(f\) et de ses dérivées vérifient l’équation.

Par exemple, la fonction \(f\) est une solution de l’équation \(\left( {{E_1}} \right)\) si :

\(\forall x \in I\), \(F\left( {x,f\left( x \right),f'\left( x \right)} \right) = 0\)

La fonction \(f\) est une solution de l’équation \(\left( {{E_2}} \right)\) si :

\(\forall x \in I\), \(F\left( {x,f\left( x \right),f'\left( x \right),f''\left( x \right)} \right) = 0\)

Définitions 3 :

· La courbe représentative de la solution d’une équation différentielle est une chronique ou** courbe intégrale**.

· Résoudre ou** intégrer** une équation différentielle c’est trouver toutes ses solutions.

L’équation différentielle la plus simple est l’équation :

\(y' = \phi \left( x \right)\)

Remarques :

· Les solutions de cette équation sont les primitives de la fonction $$ ; mais si pour une fonction $$ continue nous savons que ces primitives existent, nous ne pouvons pas toujours en donner une expression simple à l’aide des fonctions élémentaires.

· Une équation différentielle admet une infinité de solutions (c’est le cas en particulier de l’équation \(y' = \phi \left( x \right)\)). Pour trouver la solution particulière du problème étudié, il faut tenir compte des conditions particulières (ou conditions initiales) que doit satisfaire la solution. Ainsi pour une équation du premier ordre comme \(\left( {{E_1}} \right)\), la condition initiale sera en général que la solution \(f\) prend la valeur \({y_0}\) en \({x_0}\) : \(f\left( {{x_0}} \right) = {y_0}\).

Exemple :

Considérons l’équation \(y' = \phi \left( x \right)\).

Soit \(\Phi \left( x \right)\) la primitive de $$.

Les solutions de l’équations sont donc les fonctions \(\Phi \left( x \right)\), et il n’existe qu’une seule solution particulière telle que \(\Phi \left( {{x_0}} \right) = {y_0}\).

**

**

Application :

Soit \(y' = x\). Alors \(\phi \left( x \right) = x\) avec ses primitives \(\Phi \left( x \right) = \frac{{{x^2}}}{2}\).

Les solutions sont donc les fonctions \(\frac{{{x^2}}}{2} * C\) avec \(C \in \mathbb{R}\) une constante.

Pour chercher la solution particulière telle que \(\Phi \left( {{x_0}} \right) = {y_0}\) on écrit :

\(\Phi \left( {{x_0}} \right) = {y_0} \Leftrightarrow \frac{{x_0^2}}{2} + C = {y_0} \Leftrightarrow C = {y_0} - \frac{{x_0^2}}{2}\)

Ainsi, la solution particulière recherchée est la fonction définie par \({\Phi _p}\left( x \right) = \frac{{{x^2}}}{2} + {y_0} - \frac{{x_0^2}}{2}\).

2 Equations différentielles du premier ordre

Les équations différentielles d’ordre 1, on dit aussi du premier ordre, ne font intervenir que des dérivées premières : \(F\left( {x,y,y'} \right) = 0\).

2.1 Equations différentielles du premier ordre à variables séparables

La forme générale de ces équations est :

\(y' = f\left( x \right)g\left( y \right) \Leftrightarrow \frac{{dy}}{{dx}} = f\left( x \right)g\left( y \right)\)

Ainsi, on peut écrire \(\frac{{dy}}{{g\left( y \right)}} = f\left( x \right)dx\), ce qui revient à calculer deux primitives :

\(\int {\frac{{dy}}{{g\left( y \right)}}} = \int {f\left( x \right)dx} \Leftrightarrow G\left( y \right) = F\left( x \right) + C\) avec \(C \in \mathbb{R}\) une constante

Exemples :

« Résoudre l’équation \(y' = - \frac{x}{y}\)

$\begin{gathered} y’ = - \ ydy = - xdx \ = + C \ {y^2} + {x^2} = K \ \end{gathered} $

Les courbes intégrales sont donc des cercles de centres 0 et de rayon $K $.

La représentation de plusieurs courbes intégrales, pour différentes valeurs de \(K\), conduit à des cercles concentriques :

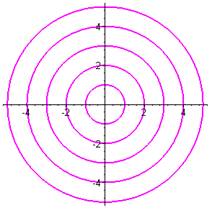Unnamed Image\(K = 1,2,3,4,5\)

« Résoudre l’équation \(y' = y\ln x\)

$ \begin{gathered} y' = y\ln x \hfill \\ \Leftrightarrow \frac{{dy}}{{dx}} * y\ln x \hfill \\ \Leftrightarrow \frac{{dy}}{y} = \ln xdx \hfill \\ \end{gathered}

$

\(\int {\ln xdx} = x\ln x - x + {C_1}\) (par une intégration par partie

\(\int {\frac{{dy}}{y}} = \ln y + {C_2}\)

Donc, on obtient :

$\begin{gathered} y * xx - x + {C_1} \ y = {e^{xx - x + {C_1}}} \ y = {e{{C_1}}}{e{xx}}{e^{ - x}} \ y = C{xx}{e{ - x}} \ \end{gathered} $

en prenant \(C = {e^{{C_1}}}\) et en utilisant le fait que \(x\ln x = \ln {x^x}\)

Les solutions de (E) sont donc les fonctions définies par \(f\left( * \right) = C{x^x}{e^{ - x}}\).

Courbe intégrale pour \(C = 1\) :

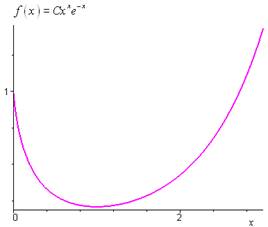
Unnamed Image

Unnamed Image

« Résoudre l’équation \(y' = \frac{6}{{{y^4}}}\)

\(\begin{gathered} y' = \frac{6}{{{y^4}}} \hfill \\ \Leftrightarrow \frac{{dy}}{{dx}} * \frac{6}{{{y^4}}} \hfill \\ \Leftrightarrow {y^4}dy = 6dx \hfill \\ \end{gathered}\)

\(\int {6dx} = 6x + {C_1}\)

\(\int {{y^4}dy} = \frac{{{y^5}}}{5} * {C_2}\)

On obtient :

\(\frac{{{y^5}}}{5} = 6x + {C_1} \Leftrightarrow {y^5} = 30x + C\) (en prenant \(C = 5{C_1}\))

Les solutions de (E) sont donc les fonctions définies par \(f\left( * \right) = \sqrt[5]{{30x + C}}\).

Courbe intégrale pour \(C = 0\) :

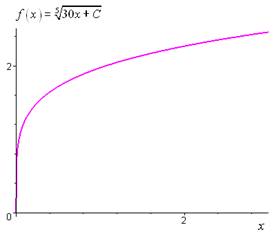
Unnamed Image

Unnamed Image

2.2 Equations différentielles du premier ordre homogènes

La forme générale de ces équations est \(y' = f\left( {\frac{y}{x}} \right) \Leftrightarrow \frac{{dy}}{{dx}} = f\left( {\frac{y}{x}} \right)\).

L’astuce consiste à poser \(u = \frac{y}{x}\) pour se ramener à une équation à variables séparables.

On pose \(u = \frac{y}{x} \Leftrightarrow y = xu\)

Ainsi, \(\frac{{dy}}{{dx}} = u + x\frac{{du}}{{dx}}\) (u est en effet une fonction de \(x\)), c’est-à-dire :

\(f\left( u \right) = u + x\frac{{du}}{{dx}}\)

Ceci qui permet alors d’écrire :

\(\frac{{du}}{{f\left( u \right) - u}} = \frac{{dx}}{x}\)

On est donc bien ramené au cas précédent.

Exemples :

« Résoudre l’équation \(y' = \frac{{{x^2} + {y^2}}}{{xy}}\)

\(y' = \frac{{{x^2} + {y^2}}}{{xy}} \Leftrightarrow \frac{{dy}}{{dx}} = \frac{{{x^2}\left( {1 + \frac{{{y^2}}}{{{x^2}}}} \right)}}{{{x^2}\left( {\frac{y}{x}} \right)}} = \frac{{1 + \frac{{{y^2}}}{{{x^2}}}}}{{\frac{y}{x}}}\)

En posant \(u = \frac{y}{x}\), il vient \(\frac{{dy}}{{dx}} = u + x\frac{{du}}{{dx}} = f\left( u \right)\) avec \(f\left( u \right) = \frac{{1 + {u^2}}}{u}\). Ainsi :

\(\frac{{du}}{{f\left( u \right) - u}} = \frac{{dx}}{x} \Leftrightarrow udu = \frac{{dx}}{x}\)

\(\int {udu} = \frac{{{u^2}}}{2} + {C_1}\)

\(\int {\frac{{dx}}{x}} = \ln x + {C_2}\)

Donc : \(\frac{{{u^2}}}{2} = \ln x + {C_2} \Leftrightarrow {u^2} = 2\ln x + {C_2}\)

On obtient finalement $u = $, c’est-à-dire $y = x $.

Représentation graphique de la solution correspondant à \(C = 0\) :

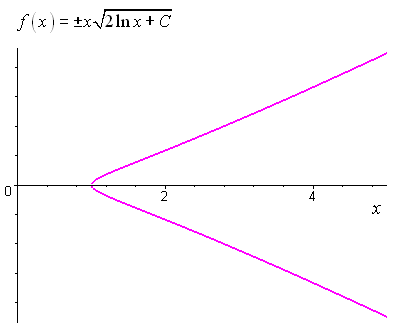
Unnamed Image

Unnamed Image

« Résoudre l’équation \(xyy' = {y^2} - {x^2}\)

\(xyy' = {y^2} - {x^2} \Leftrightarrow \frac{{dy}}{{dx}} = \frac{{{x^2}\left( {\frac{{{y^2}}}{{{x^2}}} - 1} \right)}}{{{x^2}\left( {\frac{y}{x}} \right)}} = \frac{{{u^2} - 1}}{u}\)

En posant \(u = \frac{y}{x}\), il vient \(\frac{{dy}}{{dx}} = u + x\frac{{du}}{{dx}} = \frac{{{u^2} - 1}}{u}\). Ainsi :

\(\frac{{du}}{{f\left( u \right) - u}} = \frac{{dx}}{x} \Leftrightarrow - udu = \frac{{dx}}{x}\)

\(\int { - udu} = - \frac{{{u^2}}}{2} + {C_1}\) $ $ \(\int {\frac{{dx}}{x}} = \ln x + {C_2}\)

Donc : \(\frac{{{u^2}}}{2} = - \ln x + C \Leftrightarrow {u^2} = C - 2\ln x\)

On obtient finalement $u = $, c’est-à-dire $y = x $.

Représentation graphique de la solution correspondant à \(C = 1\) :

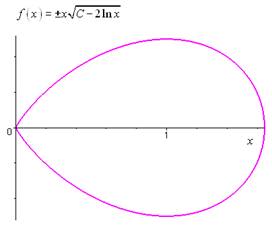
Unnamed Image

Unnamed Image

2.3 Un exemple en Biologie

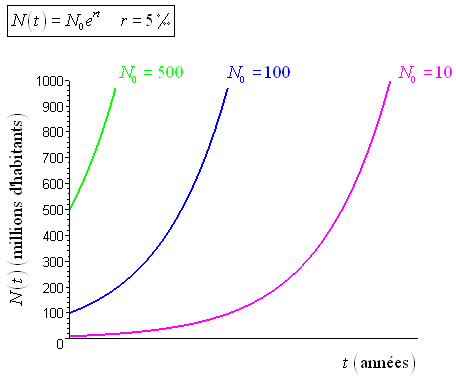
Cherchons à décrire au moyen d’une équation différentielle l’évolution de la taille de la population d’un pays qui présente les caractéristiques suivantes : par an, le taux de renouvellement est de 20 pour 1000 habitants, et le taux de mortalité est de 15 pour 1000 habitants.

Soit \(N\left( t \right)\) la taille de la population l’année \(t\), exprimée en milliers d’habitants.

La variation annuelle de la taille de la population peut être quantifiée à l’aide de la quantité \(\frac{{dN\left( t \right)}}{{dt}}\). Ainsi, on peut écrire, par le jeu d’une balance entre renouvellement naturel et mortalité :

\(\frac{{dN\left( t \right)}}{{dt}} = aN\left( t \right) - bN\left( t \right) = rN\left( t \right)\)

avec :

  • \(a\) le taux de renouvellement de la population \(a = 20\)‰ ;

  • \(b\) le taux de mortalité de la population \(b = 15\)‰ ;

  • \(r\) le taux d’accroissement absolu de la population : \(r = 5\)‰.

Pour connaître l’évolution de \(N\) en fonction de \(t\), il faut maintenant résoudre :

\(\frac{{dN}}{{dt}} = rN\) \(\left( E \right)\)

Il s’agit d’une équation différentielle à variable séparable qui s’intègre simplement :

\(\frac{{dN}}{{dt}} = rN \Leftrightarrow \frac{{dN}}{N} = rdt\)

\(\int {\frac{{dN}}{N}} = \ln N + {C_1}\)

\(\int {rdt} = rt + {C_2}\)

\(\ln N = rt + {C_2} \Leftrightarrow N\left( t \right) = K{e^{rt}}\)

La valeur de \(K\) dépend de la condition initiale choisie. Si on suppose que \(N\left( {t = 0} \right) = {N_0}\), il vient :

\(N\left( t \right) = {N_0}{e^{rt}}\)

Voici la représentation graphique de la relation \(N\) en fonction de \(t\) pour différentes valeurs de \({N_0}\) :

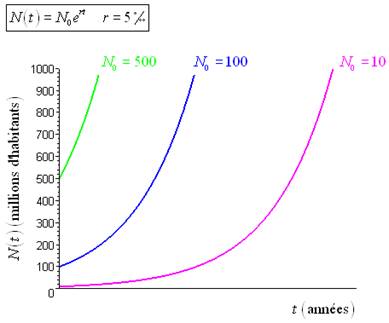
Unnamed Image

Unnamed Image

3 Equations différentielles linéaires du premier ordre

Une équation différentielle linéaire d’ordre 1 est de la forme \(y' + f\left( x \right)y = g\left( x \right)\).

On parle d’équation différentielle linéaire d’ordre 1 sans second membre si \(g\left( x \right) = 0\) (SSM).

On parle d’équation différentielle linéaire d’ordre 1 avec second membre si \(g\left( x \right) \ne 0\) (ASM).

La fonction \(g\left( x \right)\) est le second membre de l’équation. L’équation SSM est encore appelée équation homogène.

3.1 Equation différentielle linéaire sans second membre (SSM)

Nous considérons dans ce paragraphe des équations de la forme :

\(\left( {{E_0}} \right)\) : \(y' + f\left( x \right)y = 0\)

Ces équations SSM sont à variables séparables et aisément intégrables sous réserve de pouvoir calculer la primitive de la fonction \(f\) :

$\begin{gathered} y’ + f( x )y = 0 = - f( x )dx \ y = - F( x ) + C \ y = K{e^{ - F( x )}} \ \end{gathered} $

Exemples :

« Résoudre l’équation \(y' + {e^x}y = 0\)

$\begin{gathered} y’ + {e^x}y = 0 = - y{e^x} \ = - {e^x}dx y = - {e^x} + C \ y = C{e^{ * {e^x}}} \ \end{gathered} $

Représentation de la solution particulière correspondant à \(C = 1\) :

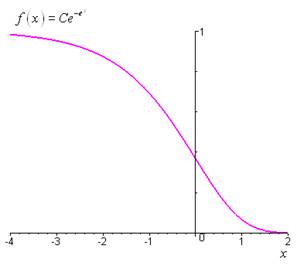
Unnamed Image

Unnamed Image

« Résoudre l’équation \(y' = {y^3}{e^x}\)

\(\begin{gathered} y' = {y^3}{e^x} \Leftrightarrow \frac{{dy}}{{dx}} = {y^3}{e^x} \hfill \\ \Leftrightarrow \frac{{dy}}{{{y^3}}} = {e^x}dx \Leftrightarrow - \frac{1}{{2{y^2}}} = {e^x} + C \hfill \\ \Leftrightarrow {y^2} = \frac{1}{{C - 2{e^x}}} \Leftrightarrow y = \pm \frac{1}{{\sqrt {C - 2{e^x}} }} \hfill \\ \end{gathered}\)

Représentation de la solution particulière correspondant à \(C = 1\) :

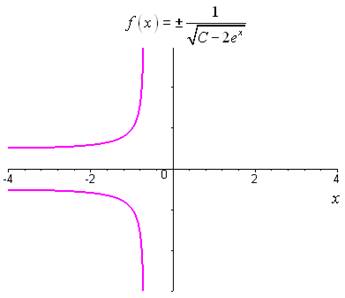
Unnamed Image

Unnamed Image

3.2 Equation différentielle linéaire avec second membre (ASM)

Nous considérons dans ce paragraphe des équations de la forme :

\(\left( E \right)\) : \(y' + f\left( x \right)y = g\left( x \right)\)

Ces équations ASM se résolvent en deux temps :

  1. On intègre d’abord l’équation SSM pour obtenir : \({y_1} = K{e^{ - F\left( x \right)}}\)

  2. On résout l’équation ASM, soit en recherchant une solution particulière \({y_p}\) de \(\left( E \right)\) (voir § 3.2.1), soit en utilisant la méthode de variation de la constante (voir § 3.2.2).

3.2.1 Recherche d’une solution particulière

Supposons que l’on dispose d’une solution particulière \({y_p}\) de \(\left( E \right)\), alors la solution générale de \(\left( * \right)\) est la fonction définie par \(y = {y_1} + {y_p} = K{e^{ - F\left( x \right)}} + {y_p}\).

Vérification :

Soit \(y = {y_1} + {y_p} = K{e^{ - F\left( x \right)}} + {y_p}\). Montrons qu’une telle fonction est bien solution de \(\left( * \right)\).

\({y_p}\) est une solution particulière de \(\left( * \right)\), elle vérifie donc \({y'_p} + f\left( x \right){y_p} = g\left( x \right)\).

Par ailleurs, \(y' = - Kf\left( x \right){e^{ - F\left( x \right)}} + {y'_p}\), donc :

$\begin{gathered} y’ + f( x )y = - Kf( x ){e^{ - F( x )}} + {{y’}_p} + f( x )[ {K{e^{ - F( x )}} + {y_p}} ] \ = - Kf( x ){e^{ - F( x )}} + Kf( x ){e^{ - F( x )}} + {{y’}_p} + f( x ){y_p} \ = {{y’}_p} + f( x ){y_p} \ = g( x ) \ \end{gathered} $

\(y = {y_1} + {y_p} = K{e^{ - F\left( * \right)}} + {y_p}\) est bien solution de \(\left( E \right)\).

Cette méthode repose entièrement sur la connaissance de \({y_p}\) qui n’est pas toujours facile à obtenir. La méthode de variation de la constante (§3.2.1) est par contre beaucoup plus générale.

Exemple :

« Résoudre l’équation \(y' + xy = {x^2} + 1\)

· On résout d’abord l’équation SSM : \(y' + xy = 0\).

$\begin{gathered} y’ + xy = 0 \ * - xy \ = * xdx \ y = - + {C_1} \ y = C{e^{ - }} \ \end{gathered} $

La solution de l’équation SSM est donc \({y_1} * C{e^{ - \frac{{{x^2}}}{2}}}\).

On cherche ensuite une solution particulière de \((E)\).

Posons ${y_p} = x + $ où \(a\) et \(b\) sont à déterminer, de telle sorte que \({y_p}\) vérifie \((E)\) :

${y’_p} = $, donc ${y’_p} * x{y_p} = + x( {x + } ) = + + $.

Par identification, il vient :

\(\left\{ \begin{gathered} \alpha = 1 \hfill \\ \alpha + \beta = 1 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} \alpha = 1 \hfill \\ \beta = 0 \hfill \\ \end{gathered} \right.\)

Une solution particulière de \(\left( E \right)\) est \({y_p} = x\).

On conclut sur la solution générale de \(\left( E \right)\) : \(y = {y_1} + {y_p} = x + C{e^{ - \frac{{{x^2}}}{2}}}\).

Représentation de la solution particulière correspondant à \(C = 1\) :

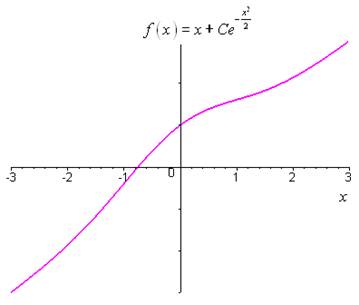
Unnamed Image

Unnamed Image

3.2.2 Méthode de variation de la constante

On utilise cette technique lorsqu’on ne peut pas trouver de solution particulière de \(\left( E \right)\). On résout dans ce cas l’équation SSM qui fournit \({y_1} = K{e^{ - F\left( x \right)}}\).

On rappelle que \(\left( E \right)\) s’écrit \(y' + f\left( x \right)y = g\left( x \right)\).

On prend alors comme fonction inconnue \(\frac{y}{{{y_1}}}\), ce qui revient à faire de \(K\), qui était constante pour l’équation SSM, une fonction inconnue de \(\left( E \right)\).

Autrement dit, on fait varier la constante.

En posant dans \(\left( E \right)\), \(y = K\left( x \right){e^{ - F\left( x \right)}}\), on obtient :

$\begin{gathered} ;y’ + f( x )y = g( x ) \ K’( x ){e^{ - F( x )}} - f( x )K( x ){e^{ - F( x )}} + f( x )K( x ){e^{ - F( x )}} = g( x ) \ K’( x ){e^{ - F( x )}} = g( x ) \ K’( x ) * g( x ){e^{F( x )}} \ \end{gathered} $

Ainsi, par intégration et sous réserve que l’on puisse calculer une primitive de \(g\left( x \right){e^{F\left( x \right)}}\), on obtient :

$K( x ) = $

Finalement, la solution générale de l’équation différentielle \(\left( E \right)\) s ‘écrit :

$y = {e^{ - F( x )}} $

Exemples :

Résoudre l’équation \(y' - \frac{y}{x} = {x^2}\)

On résout d’abord l’équation SSM : \(y' - \frac{y}{x} = 0\).

\(y' - \frac{y}{x} = 0 \Leftrightarrow \frac{{dy}}{{dx}} = \frac{y}{x} \Leftrightarrow \frac{{dy}}{y} = \frac{{dx}}{x}\)

Il vient \(\ln y = \ln x + {C_1} \Leftrightarrow {y_1} = Cx\)

On utilise ensuite la méthode de variation de la constante en cherchant \(y\) sous la forme \(y = C\left( x \right)x\).

\(y' = C'\left( x \right)x + C\left( x \right)\)

\(y' - \frac{y}{x} = {x^2} \Leftrightarrow C'\left( x \right)x + C\left( x \right) - \frac{{C\left( x \right)x}}{x} = {x^2} \Leftrightarrow C'\left( x \right) = x\)

Ainsi, on obtient \(C\left( x \right) = \frac{{{x^2}}}{2} + K\)

· On conclut que la solution générale de \(\left( * \right)\) est : \(y = \frac{{{x^3}}}{2} + Kx\).

Représentation graphique de la solution \(y = \frac{{{x^3}}}{2} + Kx\) pour \(K = 1\) :

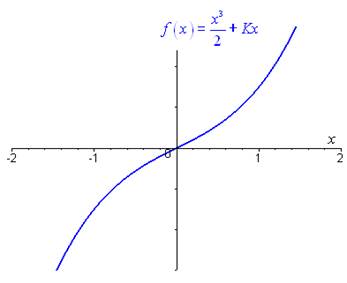
Unnamed Image

Unnamed Image

« Résoudre l’équation \(\left( {{x^2} + 1} \right)y' + 3xy = {x^2}\)

· On résout d’abord l’équation SSM : \(\left( {{x^2} + 1} \right)y' + 3xy = 0\).

\(\left( {{x^2} + 1} \right)y' + 3xy = 0 \Leftrightarrow \frac{{dy}}{{dx}} = - \frac{{3xy}}{{{x^2} + 1}} \Leftrightarrow \frac{{dy}}{y} * - \frac{{3x}}{{{x^2} + 1}}dx\)

Il vient \(\ln y = - \frac{3}{2}\ln \left( {{x^2} + 1} \right) + {C_1} \Leftrightarrow {y_1} = C{\left( {{x^2} + 1} \right) ^{-3/2}}\)

\(·\)On utilise ensuite la méthode de variation de la constante en cherchant \(y\) sous la forme \(y = C{\left( {{x^2} + 1} \right) ^{-3/2}}\) :

\(\begin{align} y' = C'(x)(x^2+1)^{3/2}-\frac{3}{2}C(x)(2x)(x^2+1)^{-5/2}\hfill\\ y' = C'(x)(x^2+1)^{3/2}- 3xC(x)(x^2+1)^{-5/2} \hfill\\ (x^2+1)y' + 3xy = x^2\Leftrightarrow C'(x)(x^2+1)^{-1/2}-3xC(x)(x^2+1)^{-3/2}+3xC(x)(x^2+1)^{-3/2}=x^2 \hfill \end{align}\)

Il reste $C’( x ) = {x^2}( {{x^2} + 1} )^{1/2} = {x^2} $.

Ainsi, $C( x ) = $.

Pour résoudre cette intégrale, on fait le changement de variable \(x = \operatorname{sh} t\), avec \(dx = \operatorname{ch} tdt\).

Il vient :

\(\begin{gathered} C\left( x \right) = \int {{{\operatorname{sh} }^2}t{{\operatorname{ch} }^2}tdt} \\ = \frac{1}{4}\int {{{\operatorname{sh} }^2}2tdt} \\ = \frac{1}{8}\int {\left( {\operatorname{ch} 4t - 1} \right)dt} \\ = \frac{1}{{32}}\operatorname{sh} 4t - \frac{1}{8}t + K \\ \end{gathered}\)

On revient alors à \(x\) avec \(t = {\text{Arg}}\operatorname{sh} x = \ln \left( x + \sqrt {{x^2} + 1} \right)\)

\(\operatorname{sh} 4t = 2\operatorname{sh} 2t\operatorname{ch} 2t = 4\operatorname{sh} t\operatorname{ch} t\left( {1 + 2{{\operatorname{sh} }^2}t} \right) = 4x\sqrt {{x^2} + 1} \left( {1 + 2{x^2}} \right)\)

Ce qui conduit à \(C\left( x \right) = \frac{x}{8}\left( {2{x^2} + 1} \right)\sqrt {{x^2} + 1} - \frac{1}{8}\ln \left( {x + \sqrt {{x^2} + 1} } \right) + K\)

· On conclut que la solution générale de \(\left( E \right)\) est :

\(y = \frac{{x\left( {2{x^2} + 1} \right)}}{{8\left( {{x^2} + 1} \right)}} - \frac{1}{8}{\left( {{x^2} + 1} \right)^{ - {3 \mathord{\left/{\vphantom {3 2}} \right.\kern-\nulldelimiterspace} 2}}}\ln \left( {x + \sqrt {{x^2} * 1} } \right) + K{\left( {{x^2} + 1} \right)^{ - {3 \mathord{\left/{\vphantom {3 2}} \right.\kern-\nulldelimiterspace} 2}}}\)

Représentation graphique de la solution pour \(K = 0\) :

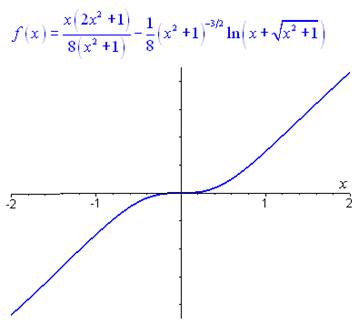
Unnamed Image

Unnamed Image

3.3 Equation différentielle linéaire du premier ordre à coefficients constants

Nous considérons cette fois-ci des équations différentielles linéaires du premier ordre à coefficients constants, c’est-à-dire de la forme :

\(\left( E \right)\) : \(y' + ay = g\left( x \right)\) avec \(a \in \mathbb{R}\) une constante.

Ce cas est un cas particulier des équations différentielle du premier ordre que nous avons vu au paragraphe 3.2. En effet, nous avons ici \(f\left( * \right) = a\).

Ainsi, après avoir résolu l’équation SSM, la méthode précédente s’applique, soit avec recherche d’une solution particulière, soit par variation de la constante.

Cependant, avec les équations différentielles linéaires du premier ordre à coefficients constants, la solution particulière \({y_p}\) s’obtient parfois simplement :

  • Si \(g\left( x \right) = P\left( x \right)\) un polynôme de degré \(n\), alors \({y_p} = Q\left( x \right)\) un polynôme de degré n ;

  • Si \(g\left( x \right) = {e^{mx}}P\left( x \right)\), alors on pose \({y_p} = {e^{mx}}z\), et \(z\) devient la fonction inconnue de l’équation différentielle \(z' + \left( {a + m} \right)z = P\left( x \right)\) : on est ramené au cas précédent.

Exemples :

« Résoudre l’équation \(y' - 2y = {x^3} + 1\)

· On résout d’abord l’équation SSM : \(y' - 2y = 0\) :

\(y' - 2y = 0 \Leftrightarrow \frac{{dy}}{{dx}} = 2y \Leftrightarrow \frac{{dy}}{y} = 2dx\)

Ainsi \(\ln y = 2x + {C_1} \Leftrightarrow {y_1} = C{e^{2x}}\)

· On cherche ensuite une solution particulière de \(\left( E \right)\).

Posons ${y_p} = + + x + $ où $,,,$ sont à déterminer pour que \({y_p}\) vérifie \(\left( * \right)\) :

${y’_p} = 3 + 2x + $

\(\begin{gathered} {{y'}_p} - 2{y_p} = 3\alpha {x^2} + 2\beta x + \gamma - 2\left( {\alpha {x^3} + \beta {x^2} + \gamma x + \delta } \right) \\ = - 2\alpha {x^3} + \left( {3\alpha - 2\beta } \right){x^2} + \left( {2\beta - 2\gamma } \right)x + \gamma - 2\delta \\\end{gathered}\)

Par identification, il vient :

\(\left\{ \begin{gathered} - 2\alpha = 1 \hfill \\ 3\alpha - 2\beta = 0 \hfill \\ 2\beta - 2\gamma = 0 \hfill \\ \gamma - 2\delta = 1 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} \alpha = -{1/2}\\ \beta = -{3/4}\\ \gamma = -{3/4}\\ \delta = -{7/8}\\ \end{gathered} \right.\)

Par conséquent, \({y_p} = - \frac{1}{2}{x^3} - \frac{3}{4}{x^2} - \frac{3}{4}x - \frac{7}{8}\).

· On conclut sur la solution générale de \(\left( E \right)\) : \(y = {y_1} + {y_p} = - \frac{1}{2}{x^3} - \frac{3}{4}{x^2} - \frac{3}{4}x - \frac{7}{8} + C{e^{2x}}\).

Représentation graphique de la solution pour \(C = 1\) :

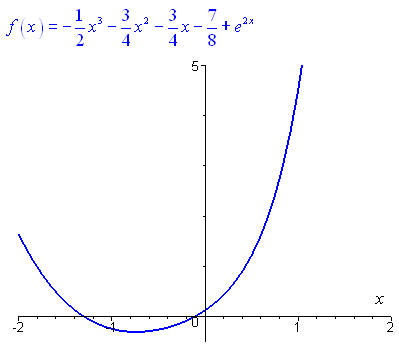
Unnamed Image

Unnamed Image

« Résoudre l’équation \(y' - 2y = {e^{2x}}\left( {{x^2} - 3x * 2} \right)\)

· On résout d’abord l’équation SSM : \(y' - 2y = 0\) (voir exemple 10) :

\({y_1} = C{e^{2x}}\)

· On cherche ensuite une solution particulière de \(\left( * \right)\).

Posons \({y_p} = {e^{2x}}z\).

\({y'_p} = \left( {z' + 2z} \right){e^{2x}}\)

\(y' - 2y = \left( {z' + 2z} \right){e^{2x}} - 2z{e^{2x}} = z'{e^{2x}}\)

Par identification, il vient : \(z' = {x^2} - 3x + 2 \Rightarrow z = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} + 2x + C\)

Ainsi, \({y_p} = \left( {\frac{{{x^3}}}{3} - \frac{3}{2}{x^2} + 2x} \right){e^{2x}}\)

· On conclut que la solution générale de \(\left( E \right)\) s’écrit : \(y = \left( {\frac{{{x^3}}}{3} - \frac{3}{2}{x^2} + 2x + C} \right){e^{2x}}\).

Représentation graphique de la solution pour \(C = 0\) :

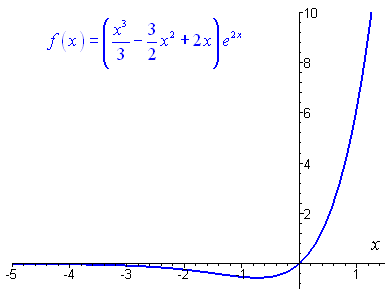
Unnamed Image

Unnamed Image

4 Compléments sur les équations différentielles du premier ordre

Nous allons voir dans ce paragraphe quatre types d’équations différentielles du premier ordre, pour lesquelles il existe des méthodes permettant de les simplifier

4.1 Equation de Bernoulli

Une équation de Bernoulli est de la forme \(y' = A\left( x \right)y + B\left( x \right){y^\alpha }\) avec \(\alpha \in \mathbb{R}\).

Lorsque \(\alpha = 0\) ou que \(\alpha * 1\), une telle équation est linéaire.

Pour \(\alpha \ne 0,1\), on peut s’arranger pour qu’elle le devienne ; on écrit :

\(y'{y^{ - \alpha }} = A\left( x \right){y^{1 - \alpha }} + B\left( x \right)\)

Or, on peut remarquer que \(y'{y^{ - \alpha }} = {\left( {\frac{{{y^{1 - \alpha }}}}{{1 - \alpha }}} \right)^\prime }\). Donc en posant \(z = {y^{1 - \alpha }}\), il vient :

\(z' = A\left( x \right)z + B\left( x \right)\) On est donc ramené à une équation linéaire que l’on sait résoudre.

Exemple :

« Résoudre l’équation \(y' = xy + x{y^2}\)

\(y' = xy + x{y^2} \Leftrightarrow y'{y^{ - 2}} = x{y^{ - 1}} * x\)

On pose \(z = {y^{ - 1}} = \frac{1}{y}\). Il vient :

\(\left( E \right)\) : \(- z' = xz + x\)

ESSM : \(z' + xz = 0 \Leftrightarrow {z_1} = C{e^{ - {x^2}/2}}\)

EASM : \({z_p} = - 1\) est une solution particulière.

On en conclut que \(z = C{e^{ - {x^2}/2}} - 1\), et donc que \(y = \frac{1}{{C{e^{{{ - {x^2}/2}}} - 1}}}\).

Représentation graphique de la solution pour \(C = 1\) :

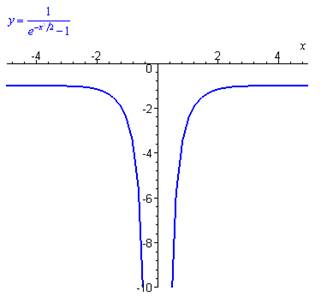
Unnamed Image

Unnamed Image

4.2 Equation de Riccati

Une équation de Riccati est de la forme \(y' = A\left( x \right){y^2} + B\left( x \right)y + C\left( x \right)\).

On ne peut la résoudre que si l’on connaît a priori une solution particulière \({y_p}\).

On pose alors \(y = {y_p} + z\), ce qui permet d’arriver à :

\(z' = A\left( x \right){z^2} + D\left( x \right)z\)

Il s’agit d’une équation de Bernoulli (voir ci-dessus).

5 Equations différentielles linéaires du second ordre

Les équations différentielles d’ordre 2 sont de la forme générale \(F\left( {x,y,y',y''} \right) = 0\).

Comme pour les équations différentielles d’ordre 1, on distingue les équations différentielles d’ordre 2 sans et avec second, puis les équations différentielles d’ordre 2 linéaires, sans et avec second membre.

La différence avec les équations différentielles d’ordre 1, tient au fait que la solution générale dépend cette fois-ci de deux constantes d’intégration.

Ainsi, pour déterminer la solution particulière d’un problème donné, il faudra disposer de deux conditions initiales, qui sont le plus souvent : \(f\left( {{x_0}} \right) = {y_0}\) et \(f'\left( {{x_0}} \right) = {z_0}\), si \(f\left( x \right)\) est une solution de l’équation différentielle.

5.1 Cas des équations incomplètes

5.1.1 Absence de y : \(F\left( {x,y',y''} \right) = 0\)

L’astuce consiste ici à poser \(z = y'\), ce qui permet de se ramener à \(F\left( {x,z,z'} \right) = 0\), qui est une équation différentielle d’ordre 1.

Ainsi, on résout si c’est possible d’abord \(F\left( {x,z,z'} \right) = 0\), ce qui donne \(z = f\left( {x,{C_1}} \right)\) ; puis on résout \(y' = z\), ce qui permet finalement d’obtenir \(y = F\left( {x,{C_1}} \right) + {C_2}\).

Exemple :

« Résoudre l’équation \(\left( {{x^2} + 1} \right)y'' + xy' * 0\)

On pose \(z = y'\), d’où \(\left( {{x^2} + 1} \right)z' + xz = 0\).

\(\left( {{x^2} + 1} \right)z' + xz = * \Leftrightarrow \frac{{dz}}{{dx}} = - \frac{{xz}}{{{x^2} + 1}} \Leftrightarrow \frac{{dz}}{z} = - \frac{{xdx}}{{{x^2} + 1}}\).

Il vient \(\ln z = - \frac{1}{2}\ln \left( {{x^2} + 1} \right) + C \Leftrightarrow z = {C_1}(x^2+1)^{-1/2}\).

Reste à résoudre \(y' = {C_1}{\left( {{x^2} + 1} \right)^{{ - 1/ 2}}} \Leftrightarrow \frac{{dy}}{{dx}} = {C_1}{\left( {{x^2} + 1} \right)^{{ - 1/2}}} \Leftrightarrow dy = \frac{{{C_1}}}{{\sqrt {{x^2} + 1} }}dx\).

Ainsi, \(y = {C_1}\arg \operatorname{sh} x + {C_2} = {C_1}\ln \left( {x + \sqrt {{x^2} + 1} } \right) + {C_2}\).

Représentation graphique de la solution pour \({C_1} * {C_2} = 1\) :

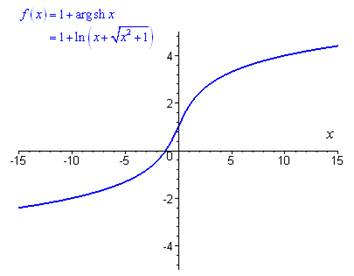
Unnamed Image

Unnamed Image

5.1.2 Absence de x : \(F\left( {y,y',y''} \right) = 0\)

On pose encore \(y' = z\), d’où \(y'' * \frac{{dz}}{{dx}} = \frac{{dz}}{{dy}}.\frac{{dy}}{{dx}} = \frac{{dz}}{{dy}}.z\) ce qui nous ramène à considérer \(z\) comme une fonction inconnue de \(y\). On est ainsi ramené à l’équation :

\(F\left( {y,z,z\frac{{dz}}{{dy}}} \right) = 0\) avec \(dx = \frac{{dy}}{z}\)

Exemple :

« Résoudre l’équation \(2yy'' = {y'^2} + 1\)

On pose \(z = y'\) ; \(y'' * z\frac{{dz}}{{dy}}\) donne \(2yz\frac{{dz}}{{dy}} = {z^2} + 1\) où les variables se séparent :

\(2yz\frac{{dz}}{{dy}} = {z^2} + 1 \Leftrightarrow \frac{{2z}}{{{z^2} + 1}}dz = \frac{{dy}}{y}\)

Ce qui donne \(\ln y = \ln \left( {{z^2} + 1} \right) + C \Leftrightarrow y = {C_1}\left( {{z^2} + 1} \right)\).

On en déduit que \(dx = \frac{{dy}}{z} = {C_1}\frac{{2zdz}}{z} = 2{C_1}dz\), ce qui conduit à \(z = \frac{x}{{2{C_1}}} + {C_2}\).

En remplaçant cette expression dans \(y\), on obtient finalement :

\(y = {C_1}\left[ {{{\left( {\frac{x}{{2{C_1}}} + {C_2}} \right)}^2} + 1} \right] = {C_1} + \frac{{{{\left( {x + 2{C_1}{C_2}} \right)}^2}}}{{4{C_1}}}\)

En re-paramétrant l’expression de \(y\), c’est-à-dire en définissant de nouvelles constantes :

\(2{C_1}{C_2} = - a\) et \(2{C_1} * b\)

On arrive finalement à l’expression de la solution générale de \(\left( E \right)\) :

\({\left( {x - a} \right)^2} = 2b\left( {y - \frac{b}{2}} \right)\)

Les courbes intégrales de ces solutions sont des paraboles. Par exemple, si \(a = b = 0\), on obtient simplement la parabole \(y = {x^2}\).

5.2 Equations différentielles d’ordre 2 linéaires sans second membre

On appelle ainsi une équation différentielle de la forme :

\(y'' + a\left( x \right)y' + b\left( * \right)y = 0\)

Ces équations ne se résolvent que si l’on dispose d’une solution particulière \({y_p}\).

Remarque :

\({y_p} * {e^x}\) est solution particulière de toute équation différentielle de la forme : * \(A\left( x \right)y'' + B\left( x \right)y' + C\left( x \right)y = 0\)

à condition que \(A\left( x \right) + B\left( x \right) + C\left( x \right) = 0\).

Connaissant \({y_p}\), on pose \(y = {y_p}z\), z devenant la nouvelle fonction inconnue de \(x\). Il en résulte :

\(y' = {y'_p}z + {y_p}z'\)

\(y'' = {y''_p}z + 2{y'_p}z' + {y_p}z''\)

Ainsi :

\(\begin{gathered} y'' + a\left( x \right)y' + b\left( x \right)y = 0 \hfill \\ \Leftrightarrow {{y''}_p}z + 2{{y'}_p}z' + {y_p}z'' + a\left( x \right)\left( {{{y'}_p}z + {y_p}z'} \right) + b\left( x \right){y_p}z \hfill \\ \Leftrightarrow {y_p}z'' + \left( {2{{y'}_p} + a\left( x \right){y_p}} \right)z' + \underbrace {\left( {{{y''}_p} + a\left( x \right){{y'}_p} + b\left( x \right){y_p}} \right)}_{\substack{ = 0 \\ {\text{car }}{y_p}{\text{ est solution}} }} z \hfill \\ \end{gathered}\)

On pose alors \(u = z'\) ce qui ramène à une équation différentielle d’ordre 1 à variables séparables :

\(\begin{gathered} {y_p}z'' + \left( {2{{y'}_p} + a\left( x \right){y_p}} \right)z' = 0 \hfill \\ \Leftrightarrow {y_p}u' = - \left( {2{{y'}_p} + a\left( x \right){y_p}} \right)u \hfill \\ \Leftrightarrow \frac{{du}}{u} = * \left( {\frac{{2{{y'}_p}}}{{{y_p}}} + a\left( x \right)} \right)dx \hfill \\ \end{gathered}\)

Ainsi, \(\ln u = - 2\ln {y_p} - \int {a\left( x \right)dx} = - 2\ln {y_p} - A\left( x \right) + C \Leftrightarrow u = {C_1}\frac{{{e^{A\left( x \right)}}}}{{{y_p}}}\).

Reste à résoudre \(z' = {C_1}\frac{{{e^{A\left( x \right)}}}}{{{y_p}}}\), c’est-à-dire \(z = {C_1}F\left( x \right) + {C_2}\), ce qui conduit finalement à la solution générale de l’équation différentielle de départ :

\(y = {y_p}\left( {{C_1}F\left( x \right) * {C_2}} \right)\)

Exemple :

« Résoudre l’équation \(\left( {x + 1} \right)y'' - \left( {2x - 1} \right)y' + \left( {x - 2} \right)y = 0\)

On constate que \({y_p} = {e^x}\) est une solution particulière de \(\left( E \right)\).

On pose \(y = {e^x}z\), d’où \(y' = {e^x}\left( {z + z'} \right)\) et \(y'' = {e^x}\left( {z + 2z' + z''} \right)\).

En remplaçant dans \(\left( E \right)\) et en simplifiant, on obtient :

\(\left( {x + 1} \right)z'' + 3z' = 0\)

On pose alors \(u = z'\), c qui donne \(\left( {x + 1} \right)u' + 3u = 0 \Leftrightarrow \frac{{du}}{u} = - \frac{3}{{x + 1}}dx\).

Ainsi, \(\ln u = - 3\ln \left( {x + 1} \right) + C \Leftrightarrow u = {C_1}{\left( {x + 1} \right)^{ - 3}} \Leftrightarrow z' = {C_1}{\left( {x + 1} \right)^{ - 3}}\).

Finalement, \(z = - \frac{{{C_1}}}{2}{\left( {x + 1} \right)^{ - 2}} + {C_2} = \frac{{{K_1}}}{{{{\left( {x + 1} \right)}^2}}} + {K_2}\).

La solution générale de \(\left( E \right)\) est donc \(y = {e^x}\left( {\frac{{{K_1}}}{{{{\left( {x + 1} \right)}^2}}} + {K_2}} \right)\).

Représentation de la courbe intégrale pour \({K_1} * {K_2} = 1\) :

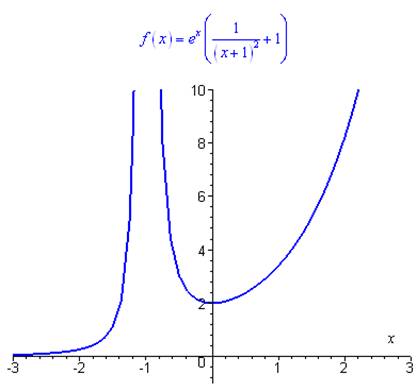
Unnamed Image

Unnamed Image

5.3 Equations différentielles d’ordre 2 linéaires sans second membre à coefficients constants

On désigne ainsi une équation différentielle de la forme :

\(\left( E \right)\) : \(y'' + ay' + by = 0\) avec \(a,b \in \mathbb{R}\) des constantes

5.3.1 Etude du cas où \(a = 0\)

· Si \(b = 0\), alors \(\left( E \right)\) devient \(y'' = 0\), ce qui donne \(y = {C_1}x + {C_2}\).

· Si \(b > 0\), on peut poser \(b = {\omega ^2}\) avec \(\omega > 0\), ce qui conduit à \(y'' + {\omega ^2}y = 0\). Cette équation admet deux solutions particulières simples \({y_{p1}} = \sin \left( {\omega x} \right)\) et \({y_{p2}} = \cos \left( {\omega x} \right)\). La solution générale de \(\left( * \right)\) est donc \(y = {C_1}\sin \left( {\omega x} \right) + {C_2}\cos \left( {\omega x} \right)\).

· Si \(b < 0\), on pose alors \(b = * {\omega ^2}\) avec \(\omega > 0\), ce qui conduit à \(y'' - {\omega ^2}y = 0\). Cette équation admet deux solutions particulières simples \({y_{p1}} = {e^{\omega x}}\) et \({y_{p2}} = {e^{ - \omega x}}\). La solution générale de \(\left( * \right)\) est donc \(y = {C_1}{e^{\omega x}} + {C_2}{e^{ * \omega x}}\).

5.3.2 Etude du cas où \(a \ne 0\)

On revient donc à \(\left( E \right)\) : \(y'' * ay' + by = 0\).

En inspirant de ce qui précède, on peut imaginer de chercher des solutions sous la forme \(y = {e^{rx}}\) avec \(r\) une constante.

En remplaçant \(y = {e^{rx}}\) dans \(\left( * \right)\) puis en simplifiant par \({e^{rx}}\), on obtient l’équation :

\(\varphi \left( r \right) = {r^2} + ar + b = 0\) : équation caractéristique de \(\left( E \right)\)

La nature des solutions de \(\left( E \right)\) dépend alors de la nature des solutions de \(\varphi \left( r \right) = 0\).

On note \(\Delta = {a^2} - 4b\) le discriminant de l’équation caractéristique.

· Si \(\Delta = {a^2} - 4b > 0\), alors \(\varphi \left( r \right) = 0\) admet deux racines réelles distinctes \({r_1},{r_2}\), et \(\left( E \right)\) admet deux solutions particulières \({y_{p1}} * {e^{{r_1}x}}\) et \({y_{p2}} = {e^{{r_2}x}}\). La solution générale de \(\left( E \right)\) est donc \(y = {C_1}{e^{{r_1}x}} + {C_2}{e^{{r_2}x}}\).

· Si \(\Delta = {a^2} - 4b = 0\), alors \(\varphi \left( r \right) = 0\) admet une racine double \({r_0} * - \frac{a}{2}\) et \(\left( E \right)\) admet la solution particulière \({y_p} = {e^{{r_0}x}}\). En posant \(y = {e^{{r_0}x}}z\), on montre que la solution générale de \(\left( E \right)\) est \(y = \left( {{C_1}x + {C_2}} \right){e^{{r_0}x}}\).

· Si \(\Delta = {a^2} - 4b < 0\), alors \(\varphi \left( r \right) = 0\) admet deux racines complexes conjuguées ${r_{1,2}} * i$. La solution générale de \(\left( * \right)\) s’écrit alors \(y = {e^{\alpha x}}\left( {{C_1}\sin \beta x + {C_2}\cos \beta x} \right)\).

Exemple :

« Résoudre l’équation \(y'' - 2y' + y = 0\)

L’équation caractéristique s’écrit \({r^2} * 2r + 1 = 0 \Leftrightarrow {\left( {r - 1} \right)^2} = 0\).

Elle admet une racine double \({r_0} * 1\).

Par conséquent, la solution générale de l’équation différentielle est :

\(y = \left( {{C_1}x + {C_2}} \right){e^x}\)

5.4 Equations différentielles d’ordre 2 linéaires avec second membre « simple » et à coefficients constants

On appelle dans ce paragraphe des équations différentielles de la forme :

\(y'' + ay' + by = f\left( x \right)\)

Ces équations ASM se résolvent en deux temps :

  1. On intègre d’abord l’équation SSM (§ 5.3.) ; on obtient \({y_1}\).

  2. On résout l’équation ASM en recherchant une solution particulière \({y_p}\) de \(\left( * \right)\) (voir Chapitre * § 6) et dans ce cas \(y = {y_p} + {y_1}\).

Nous allons voir à partir d’un exemple, comment mettre en œuvre la recherche d’une solution particulière.

Considérons l’équation suivante :

\(\left( E \right)\): \(y'' * 2y' + y = 2{x^2} - x - 1\)

1. Résolution de l’équation SSM : voir exemple ci-dessus :

\({y_1} = \left( {{C_1}x + {C_2}} \right){e^x}\)

2. On cherche alors une solution \({y_p}\) sous la forme \({y_p} = a{x^2} + bx + c\),c’est-à-dire une solution particulière de la forme du second membre ; on cherche alors les coefficients \(a\), \(b\), et \(c\) pour que \({y_p}\) soit solution de \(\left( E \right)\) :

\({y_p} = a{x^2} + bx + c\)

\({y'_p} = 2ax + b\)

\({y''_p} = 2a\)

Ainsi :

\(\begin{gathered}\)

  • {{y’’}_p} - 2{{y’}_p} + {y_p} = 2a - 2( {2ax + b} ) + a{x^2} + bx + c \$

  • = a{x^2} + ( {b - 4a} )x + c + 2a - 2b \$

$\end{gathered} $

En identifiant, \(a{x^2} + \left( {b - 4a} \right)x + * + 2a - 2b\) avec \(g\left( x \right) = 2{x^2} - x - 1\), on obtient :

\(a = 2\) \(b = 7\) \(c = 9\)

On en déduit que \({y_p} = 2{x^2} + 7x + 9\) est une solution particulière de \(\left( E \right)\).

3. On conclut que la solution générale de \(\left( * \right)\) est \(y = {y_p} + {y_1}\), c’est-à-dire:

\(y = \left( {{C_1}x + {C_2}} \right){e^x} + 2{x^2} + 7x + 9\)

6 Solutions particulières

Nous allons résumer dans un tableau les solutions particulières possibles dans le cas d’équations différentielles avec un second membre (ASM) « simple ».

Equation différentielle du premier ordre linéaire à coefficients constants :

\(y' + ay = f\left( x \right)\)

Solution particulière

Soit \(\phi \left( r \right) = r + a\) l’équation caractéristique

Second membre de la forme :

\(f\left( x \right) = P\left( x \right)\) avec \(d^\circ P = n\) *

\({y_p} = {x^k}P\left( x \right)\)

\(k = 0\) si 0 n’est pas solution de l’équation \(\phi \left( r \right) = 0\)

\(k = 1\) si 0 est solution de l’équation \(\phi \left( r \right) = 0\)

Second membre de la forme :

\(f\left( x \right) = {e^{\alpha x}}P\left( x \right)\) avec \(d^\circ P = n\) *

\({y_p} = {x^k}{e^{\alpha x}}P\left( x \right)\)

\(k = 0\) si \(a\) n’est pas solution de l’équation \(\phi \left( r \right) = 0\)

\(k = 1\) si \(a\) est solution de l’équation \(\phi \left( r \right) = 0\)

Second membre de la forme :

\(f\left( x \right) = A\cos \beta x + B\sin \beta x\) *

\({y_p} = C\cos \beta x + D\sin \beta x\)

Equation différentielle du premier ordre linéaire à coefficients constants :

\(y'' + ay' + by = f\left( x \right)\)

Solution particulière

Soit \(\phi \left( r \right) = {r^2} + ar + b\)** l’équation caractéristique**

Second membre de la forme :

\(f\left( x \right) = P\left( x \right)\) avec \(d^\circ P = n\) *

\({y_p} = {x^k}P\left( x \right)\)

\(k = 0\) si 0 n’est pas solution de l’équation \(\phi \left( r \right) = 0\)

\(k = 1\) si 0 est une racine de l’équation \(\phi \left( r \right) = 0\)

\(k = 2\) si 0 est racine double de l’équation \(\phi \left( r \right) = 0\)

Second membre de la forme :

\(f\left( x \right) = {e^{\alpha x}}P\left( x \right)\) avec \(d^\circ P = n\) *

\({y_p} = {x^k}{e^{\alpha x}}P\left( x \right)\)

\(k = 0\) si \(a\) n’est pas solution de l’équation \(\phi \left( r \right) = 0\)

\(k = 1\) si \(a\) est une racine de l’équation \(\phi \left( r \right) = 0\)

\(k = 2\) si \(a\) est racine double de l’équation \(\phi \left( r \right) = 0\)

7 Exemples d’applications en Biologie

7.1 Exemple en Démographie

Il est possible de décrire au moyen d’une équation différentielle l’évolution de la taille de la population d’un pays qui présente les caractéristiques suivantes : par an, le taux de renouvellement est de 20 pour 1000 habitants, et le taux de mortalité est de 15 pour 1000 habitants.

Soit \(N\left( t \right)\) la taille de la population l’année \(t\), exprimée en milliers d’habitants.

La variation annuelle de la taille de la population peut être quantifiée à l’aide de la quantité \(\frac{{dN\left( t \right)}}{{dt}}\).

Ainsi, on peut écrire, par le jeu d’une balance entre renouvellement naturel et mortalité :

\(\frac{{dN\left( t \right)}}{{dt}} = aN\left( t \right) - bN\left( t \right) = rN\left( t \right)\)

avec :

\(-\)a$ le taux de renouvellement de la population \(a = 20{\raise0.7ex\hbox{\)^\(} \!\mathord{\left/\)

\(-\){}.-}$

  • \(\!\lower0.7ex\hbox{\){}\(}}\) ;

\(-\)b$ le taux de mortalité de la population \(b = 15{\raise0.7ex\hbox{\)^\(} \!\mathord{\left/\)

\(-\){}.-}$

  • \(\!\lower0.7ex\hbox{\){}\(}}\) ;

\(-\)r le taux d’accroissement absolu de la population : \(r = 5{\raise0.7ex\hbox{\)^\(} \!\mathord{\left/\)

\(-\){}.-}$

  • \(\!\lower0.7ex\hbox{\){}\(}}\).

Pour connaître l’évolution de \(N\) en fonction de \(t\), il faut maintenant résoudre :

\(\frac{{dN}}{{dt}} = rN\) \(\left( * \right)\)

Il s’agit d’une équation différentielle à variable séparable qui s’intègre simplement :

\(\frac{{dN}}{{dt}} = rN \Leftrightarrow \frac{{dN}}{N} = rdt\)

\(\int {\frac{{dN}}{N}} = \ln N + {C_1}\)

\(\int {rdt} = rt + {C_2}\)

\(\ln N = rt + {C_2} \Leftrightarrow N\left( t \right) = K{e^{rt}}\)

La valeur de \(K\) dépend de la condition initiale choisie. Si on suppose que \(N\left( {t = 0} \right) = {N_0}\), il vient :

\(N\left( t \right) = {N_0}{e^{rt}}\)

Voici la représentation graphique de la relation \(N\) en fonction de \(t\) pour différentes valeurs de \({N_0}\) :

Unnamed Image

Unnamed Image

7.2 Exemples en Ecologie

7.2.1 Croissance pondérale d’un organisme

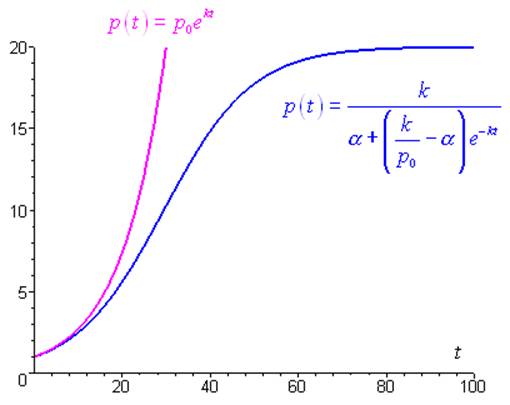
Pendant une période \(t = 0\) à \(t = {t_1}\) du développement d’un organisme, on admet que la vitesse de croissance pondérale est proportionnelle à son poids. On obtient alors ‘équation suivante :

\(\frac{{dp}}{{dt}} = kp\) avec \(p\) le poids (en \(g\)) et \(k\) le taux d’accroissement (I)

Le temps est exprimé en jours.

On sait d’autre part qu’à \(t = 0\), \(p = {p_0}\).

Cette équation à variables séparables s’intègre facilement (voir ci-dessus) :

\(p\left( t \right) = {p_0}{e^{kt}}\)

  • l’aide de mesure faites sur un grand nombre d’individus, on a obtenu les résultats suivants :

  • \(t = 0\), \(p = {p_0} = 1\;g\)

  • \(t = 10\;{\text{jours}}\), \(p = 2.718\;g\)

Ces données expérimentales permettent d’estimer une valeur pour \(k\) : \(k \simeq 0.1\;{\left( {{\text{jours}}} \right)^{ - 1}}\).

On peut ainsi tracer grossièrement l’évolution du poids de l’organisme au cours de la croissance (courbe rose) :

Unnamed Image

Unnamed Image

Cependant, il paraît peu probable que la croissance pondérale de l’organisme considère soit aussi rapide, et surtout illimitée. On est alors amené à proposer une autre équation, qui fait intervenir un terme de ralentissement de la croissance :

\(\frac{{dp}}{{dt}} = \underbrace {kp}_{croissance} - \underbrace {\alpha {p^2}}_{ralentissement}\) (II)

Cette équation est aussi à variables séparables :

\(\frac{{dp}}{{dt}} = p\left( {k - \alpha p} \right) \Leftrightarrow \frac{{dp}}{{p\left( {k - \alpha p} \right)}} = dt\)

Pour intégrer l’équation, il faut alors faire une décomposition en éléments simples :

\(\frac{1}{{p\left( {k - \alpha p} \right)}} = \frac{1}{{kp}} * \frac{\alpha }{{k\left( {k - \alpha p} \right)}}\)

Ainsi :

$ = + = $

\(\ln p - \ln \left( {k - \alpha p} \right) = kt + C\)

\(\frac{p}{{k - \alpha p}} = C{e^{kt}}\)

On obtient finalement :

\(p\left( t \right) = \frac{k}{{\alpha + \left( {\frac{k}{{{p_0}}} - \alpha } \right){e^{ - kt}}}}\)

Une rapide étude de cette fonction permet de voir que :

\(p\left( 0 \right) = {p_0}\) (ce que l’on attendait) et \(\mathop {\lim }\limits_{t \to + \infty } p\left( t \right) * \frac{k}{\alpha }\)

Enfin, par un raisonnement simple, on montre que pour des temps petits (proches de \(t = 0\)), on a \(p\left( * \right) = {p_0}{e^{kt}}\). Ceci signifie que les courbes intégrales des équations (\(I\)) et (II) sont confondues pour des valeurs de \(t\) faibles (voir courbe bleue).

7.2.2 Probabilité de rencontre

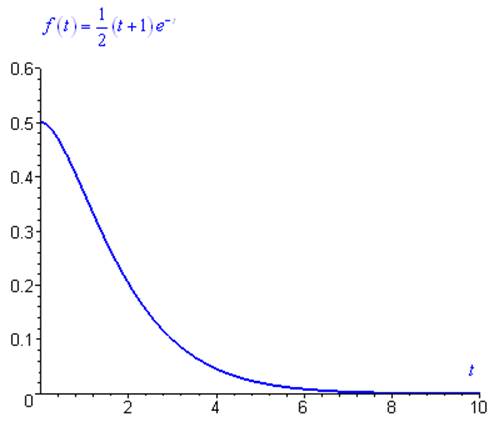
On désigne par \(f\) la densité de probabilité de rencontre entre deux animaux dans des conditions déterminées (par exemple en laboratoire). On suppose que cette densité de probabilité est fonction du temps :

\(f\left( t \right) = \frac{1}{2}\left( {t + 1} \right){e^{ - t}}\)

Une rapide étude de fonction conduit à la représentation graphique suivante :

Unnamed Image

Unnamed Image

On peut alors calculer la probabilité \(p\) que deux animaux se rencontrent entre les instants \({t_1}\) et \({t_2}\) à l’aide de l’intégrale suivante :

$p = _{{t_1}}^{{t_2}} {f( t )dt} $

Ainsi, $_0^{ + } {f( * )dt} $ est nécessairement égale à 1 (probabilité que deux animaux se rencontrent entre \(t = 0\) et l’infini) :

$_0^{ + } {f( t )dt} = _0^{ + } {( {t + 1} ){e^{ - t}}dt} $

Ce calcul s’effectue à l’aide d’une intégration par partie :

On pose \(u\left( t \right) = t + 1\) et \(v'\left( t \right) = {e^{ - t}}\). Il vient \(u'\left( * \right) = 1\) et \(v\left( t \right) = - {e^{ - t}}\).

Ainsi, $_0^{ + = [ { - ( {t + 1} ){e^{ - t}}} ]_0^{ + } - _0^{ + $. En tenant compte du fait que \(\mathop {\lim }\limits_{t \to + \infty } {e^{ - t}} = 0\), on obtient :*

\(\int\limits_0^{ + \infty } {f\left( t \right)dt} = 1\)

Pour revenir aux équations différentielles, on peut chercher à résoudre l’équation suivante :

\(f'' + 2f' + f = 0\)

L’équation caractéristique est \(\phi \left( r \right) = {r^2} + 2r + 1 = {\left( {r + 1} \right)^2}\), ce qui conduit immédiatement à la solution générale :

\(f\left( x \right) = \left( {{C_1}x + {C_2}} \right){e^{ - x}}\)

Si on cherche la solution particulière telle que \(f\left( * \right) = \frac{1}{2}\) et \(f'\left( 0 \right) = 0\), on retrouve exactement :

\(f\left( x \right) = \frac{1}{2}\left( {x + 1} \right){e^{ - x}}\)