Chapitre 5 : Statistique descriptive
1 Introduction
La statistique est une méthode scientifique qui consiste à réunir des données chiffrées sur des ensembles nombreux, puis à analyser, à commenter et à critiquer ces données. Il ne faut pas confondre la statistique qui est la science qui vient d’être définie et une statistique qui est un ensemble de données chiffrées sur un sujet précis.
Les premières statistiques correctement élaborées ont été celles des recensements démographiques. Ainsi le vocabulaire statistique est essentiellement celui de la démographie.
Les ensembles étudiés sont appelés population. Les éléments de la population sont appelés individus ou unités statistiques. La population est étudiée selon un ou plusieurs caractères.
Les statistiques descriptives peuvent se résumer par le schéma suivant :

2 Echantillonnage statistique
Pour recueillir des informations sur une population statistique, l’on dispose de deux méthodes :
la méthode exhaustive ou recensement où chaque individu de la population est étudié selon le ou les caractères étudiés.
la méthode des sondages ou échantillonnage qui conduit à n’examiner qu’une fraction de la population, un échantillon.
2.1 Définition
L’échantillonnage représente l’ensemble des opérations qui ont pour objet de prélever un certain nombre d’individus dans une population donnée.
Pour que les résultats observés lors d’une étude soient généralisables à la population statistique, l’échantillon doit être représentatif de cette dernière, c’est à dire qu’il doit refléter fidèlement sa composition et sa complexité. Seul l’échantillonnage aléatoire assure la représentativité de l’échantillon.
Un échantillon est qualifié d’aléatoire lorsque chaque individu de la population a une probabilité connue et non nulle d’appartenir à l’échantillon.
Le cas particulier le plus connu est celui qui affecte à chaque individu la même probabilité d’appartenir à l’échantillon.
2.2 Echantillonnage aléatoire simple
L’échantillonnage aléatoire simple est une méthode qui consiste à prélever au hasard et de façon indépendante, \(n\) individus ou unités d’échantillonnage d’une population à \(N\) individus.
Chaque individu possède ainsi la même probabilité de faire partie d’un échantillon de \(n\) individus et chacun des échantillons possibles de taille \(n\) possède la même probabilité d’être constitué.
L’échantillonnage aléatoire simple assure l’indépendance des erreurs, c’est-à-dire l’absence d’autocorrélations parmi les données relatives à un même caractère. Cette indépendance est indispensable à la validité de plusieurs tests statistiques (chapitre 7).
Exemple :
Les données météorologiques ne sont pas indépendantes puisque les informations recueillies sont d’autant plus identiques qu’elles sont rapprochées dans le temps et dans l’espace. *
Il existe d’autres techniques d’échantillonnage que nous ne développerons pas dans un premier temps dans ce cours comme l’échantillonnage systématique ou l’échantillonnage stratifié qui répondent à des problématiques biologiques spécifiques.
3 Les caractères statistiques
3.1 Définition
On appelle caractère statistique simple toute application :
\(X : P \longrightarrow \mathbb{R}\)
avec \(P\) un ensemble fini appelé population ; tout élément \(\omega\) de \(P\) s’appelle un individu.
Le caractère désigne une grandeur ou un attribut, observable sur un individu et susceptible de varier prenant ainsi différents états appelés modalités.
On appelle modalité toute valeur :
\(x_i \in X(P)\)
telle que : \(X (P) = {x_1 ,x_2 ,x_3 ,....., x_i ,...., x_k }\) avec \(k\) nombre de modalités différentes de \(X\)
Remarque : Seuls les caractères quantitatifs ont valeurs dans R, les caractères qualitatifs s’y ramenant par un codage.
Exemple :
Lors des recensements, les caractères étudiés sont l’âge, le sexe, la qualification professionnel, etc. Le caractère « sexe » présente deux modalités alors que pour la qualification professionnelle, le nombre de modalités va dépendre de la précision recherchée.
3.1.1 Les caractères qualitatifs
Mesurées dans une échelle nominale, les modalités sont exprimables par des noms et ne sont pas hiérarchisées. Un caractère nominal peut être dichotomique s’il ne peut prendre que deux modalités.
Exemple: la couleur du pelage, les groupes sanguins, les différents nucléotides de l’ADN, la présence ou l’absence d’un caractère (dichotomique), etc.
Mesurées dans une échelle ordinale: les modalités traduisent le degré d’un état caractérisant un individu sans que ce degré ne puisse être défini par un nombre qui résulte d’une mesure. Les modalités sont alors hiérarchisées.
Exemple: le stade d’une maladie.
Certains tests (non vus dans ce cours) permettent de profiter de cette information et sont alors plus puissants que des tests sur variable nominale.
3.1.2 Les caractères quantitatifs
Le caractère est discret s’il peut prendre seulement certaines valeurs dans un intervalle donné. En général il résulte d’un comptage ou dénombrement.
Exemple: le nombre de petits par portée, le nombre de cellules dans une culture, le nombre d’accidents pour une période donnée, etc.
Remarque : Attention, un caractère quantitatif discret peut résulter de la transformation d’un caractère nominal (ex. comptage des individus porteurs ou non d’un caractère).
Le caractère est continu s’il peut théoriquement prendre n’importe quelle valeur dans un intervalle donné. En général il résulte d’une mesure.
Exemple: le poids, la taille, le taux de glycémie, le rendement, etc.
Remarque : En réalité le nombre de valeurs possibles pour un caractère donné dépend de la précision de la mesure. On peut considérer comme continu un caractère discret qui peut prendre un grand nombre de valeurs.
Exemple: le nombre de globules blancs ou rouges par ml de sang, le nombre de nucléotides A dans une très longue séquence d’ADN (plusieurs Mégabases).
3.2 Liens avec les concepts probabilistes
Les concepts qui viennent d’être présentés sont les homologues de concepts du calcul des probabilités et il est possible de disposer en regard les concepts homologues (voir table ci-dessous).

Ainsi la notion de caractère se confond avec celle de variable aléatoire.
4 Représentation des données
Il existe plusieurs niveaux de description statistique : la présentation brute des données, des présentations par tableaux numériques, des représentations graphiques et des résumés numériques fournis par un petit nombre de paramètres caractéristiques.
4.1 Séries statistiques
Une série statistique correspond aux différentes modalités d’un caractère sur un échantillon d’individus appartenant à une population donnée.
Le nombre d’individus qui constituent l’échantillon étudié s’appelle la taille de l’échantillon.
Exemple :
Afin d’étudier la structure de la population de gélinottes huppées (Bonasa umbellus) abattues par les chasseurs canadiens, une étude du dimorphisme sexuel de cette espèce a été entreprise. Parmi les caractères mesurés figure la longueur de la rectrice centrale (plume de la queue). Les résultats observés exprimés en millimètres sur un échantillon de 50 mâles juvéniles sont notés dans la série ci-dessus :

4.2 Tableaux statistiques
Le tableau de distribution de fréquences est un mode synthétique de présentation des données. Sa constitution est immédiate dans le cas d’un caractère discret mais nécessite en revanche une transformation des données dans le cas d’un caractère continu.
4.2.1 Fréquences absolues, relatives et cumulées
A chaque modalité du caractère \(X\), peut correspondre un ou plusieurs individus dans l’échantillon de taille \(n\).
On appelle effectif de la modalité \(x_i\), le nombre \(n_i\) où \(n_i\) est le nombre d’individu \(\omega\)
tel que \(X(\omega) = x_i\)
Remarque : Parfois on peut rencontrer le terme de fréquence absolue pour les effectifs.
On appelle fréquence de la modalité \(x_i\), le nombre \(f_i\) tel que \({f_i} = \frac{n_i}{n}\)
Remarque : Parfois on peut rencontrer le terme de fréquence relative pour les fréquences. Le pourcentage est une fréquence exprimée en pour cent. Il est égal à \(100 f_i\).
L’emploi des fréquences ou fréquences relatives s’avère utile pour comparer deux distributions de fréquences établies à partir d’échantillons de taille différente.
On appelle fréquences cumulées ou fréquences relatives cumulées en \(x_i\),
le nombre \(f_i\text{cum}\) tel que \(f_i\text{cum} = \sum\limits_{p = 1}^i {f_p}\)
Remarque : On peut noter que \(\sum\limits_{i = 1}^k {n_i} = n\), taille de l’échantillon et \(\sum\limits_{i = 1}^k {{f_i}} = 1\)
4.2.2 Caractères quantitatifs discrets
Dans le cas d’un caractère quantitatif discret, l’établissement de la distribution des données observées associées avec leurs fréquences est immédiate.
Exemple :

La cécidomyie du hêtre provoque sur les feuilles de cet arbre des galles dont la distribution de fréquences observées est la suivante :

La taille de l’échantillon étudié est \(n=375\) feuilles
4.2.3 Caractères quantitatifs continues
Dans le cas d’un caractère quantitatif continu, l’établissement du tableau de fréquences implique d’effectuer au préalable une répartition en classes des données. Cela nécessite de définir le nombre de classes attendu et donc l’amplitude associée à chaque classe ou intervalle de classe.
En règle générale, on choisit des classes de même amplitude. Pour que la distribution en fréquence est un sens, il faut que chaque classe comprenne un nombre suffisant de valeurs (\(n_i\)).
Diverses formules empiriques permettent d’établir le nombre de classes pour un échantillon de taille \(n\).
La règle de STURGE : Nombre de classes = \(1 + (3,3 \log n)\)
La règle de YULE : Nombre de classes = \(2,5 \sqrt[4]{n}\)
L’intervalle entre chaque classe est obtenu ensuite de la manière suivante :
Intervalle de classe = (\(X\) max - \(X\) min) / Nombre de classes
avec \(X\) max et \(X\) min, respectivement la plus grande et la plus petite valeur de \(X\) dans la série statistique.
A partir de \(X\)min on obtient les limites de classes ou bornes de classes par addition successive de l’intervalle de classe. En règle général, on tente de faire coïncider l’indice de classe ou valeur centrale de la classe avec un nombre entier ou ayant peu de décimales.
Exemple:
Dans le cadre de l’étude de la population de gélinottes huppées (Bonasa umbellus), les valeurs de la longueur de la rectrice principale peuvent être réparties de la façon suivante :
- définition du nombre de classes :
Règle de Sturge : \(1 + (3,3 \log 50) = 6,60\)
Règle de Yule : \(2,5 \sqrt[4]{50} = 6,64\) les deux valeurs sont très peu différentes
- définition de l’intervalle de classe :
IC = \(\frac{{174 - 140}}{{6,6}}\) = 5,15 mm que l’on arrondit à 5 mm par commodité
- Tableau de distribution des fréquences
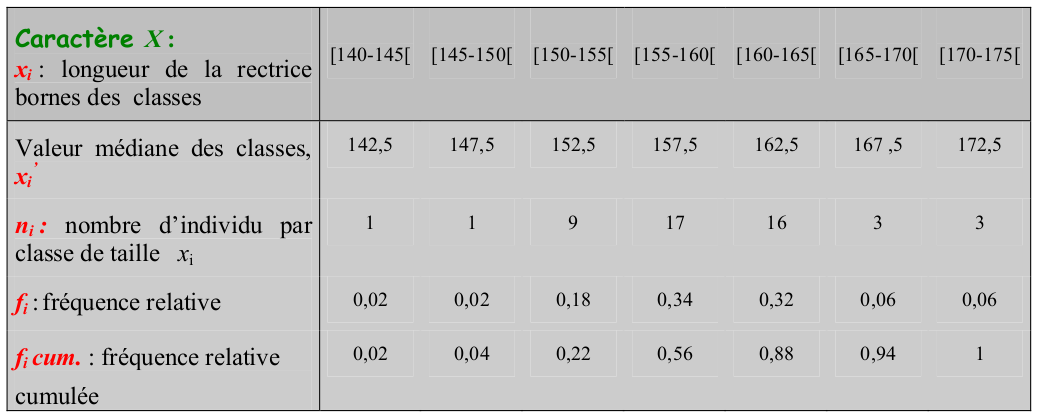
4.3 Représentations graphiques
Les représentations graphiques ont l’avantage de renseigner immédiatement sur l’allure générale de la distribution. Elles facilitent l’interprétation des données recueillies.
4.3.1 Caractères quantitatifs discrets
Pour les caractères quantitatifs discrets, la représentation graphique est le diagramme en bâtons où la hauteur des bâtons correspond à l’effectif \(n_i\) associé à chaque modalité du caractère \(x_i\).
Exemple :

Dans l’exemple de la cécidomyie du hêtre, la distribution des fréquences observées du nombre de galles par feuille peut être représentée par un diagramme en bâtons avec en ordonnée les effectifs \(n_i\) et en abscisse les différentes modalités de la variable étudiée.
4.3.2 Caractères quantitatifs continus
Pour les caractères quantitatifs continus, la représentation graphique est l’histogramme où la hauteur du rectangle est proportionnelle à l’effectif n_i. Ceci n’est vrai que si l’intervalle de classe est constant. Dans ce cas l’aire comprise sous l’histogramme s’avère proportionnelle à l’effectif total. En revanche lorsque les intervalles de classe sont inégaux, des modifications s’imposent pour conserver cette proportionnalité. Dans ce cas, en ordonnée, au lieu de porter l’effectif, on indique le rapport de la fréquence sur l’intervalle de classe. Ainsi la superficie de chaque rectangle représente alors l’effectif associé à chaque classe.
Exemple :
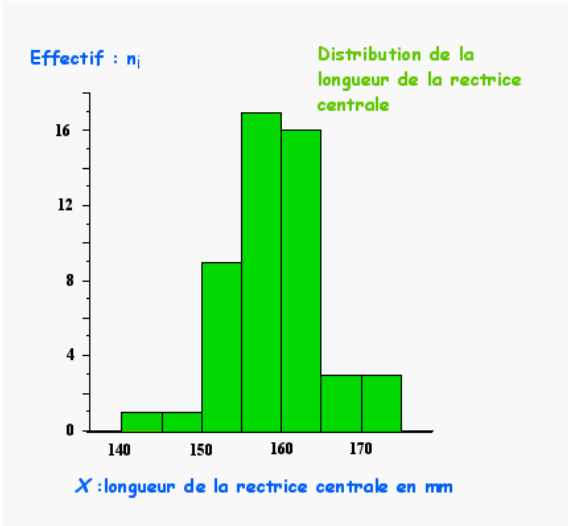
Dans l’exemple de la longueur de la rectrice centrale des individus mâles de la gélinotte huppée, la distribution des fréquences observées est représentée par un histogramme avec en ordonnée les effectifs \(n_i\) et en abscisse les limites de classe de la variable étudiée.
5 Indicateurs numériques
Le dernier niveau de description statistique est le résumé numérique d’une distribution statistique par des indicateurs numériques ou paramètres caractéristiques.
Remarque : Ces derniers représentent une transition entre la statistique purement descriptive et l’estimation des paramètres qui caractérisent les distributions de probabilité (chapitre 6).
5.1 Indicateur de position
Ces paramètres ont pour objectif dans le cas d’un caractère quantitatif de caractériser l’ordre de grandeur des observations.
5.1.1 La moyenne arithmétique
Soit un échantillon de \(n\) valeurs observées \(x_1 , x_2 , ....,x_i ,....,x_n\) d’un caractère quantitatif \(X\), on définit sa moyenne observée \(\bar{x}\) comme la moyenne arithmétique des \(n\) valeurs :
\(\bar{x}= \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}_{}}\)
Remarque : Une des propriétés de la moyenne arithmétique est que la somme des écarts à la moyenne est nulle: \(\sum\limits_{i = 1}^n {\left( {{x_i} - \bar{x}}\right)} = 0\)
Si les données observées \(x_i\) sont regroupées en \(k\) classes d’effectif \(n_i\) (caractère continu regroupé en classe ou caractère discret), il faut les pondérer par les effectifs correspondants:
\(\bar{x}= \frac{1}{n}\sum\limits_{i = 1}^k {{n_i}{x_i}}\) avec \(n = \sum\limits_{i = 1}^k {{n_i}}\)
Exemples :
Dans le cas de l’étude du dimorphisme sexuel de la gélinotte huppée, la longueur moyenne de la rectrice principale du mâle juvénile est :
- dans le cas des données non groupées :
\(\bar{x}= \frac{{153 + 165 + 160 + ..... + 171 + 164 * 158}}{{50}} = \frac{{7943}}{{50}} =\) 158,9 mm
- dans le cas des données groupées où les valeurs \(x_i\) correspondent aux valeurs médianes des classes,
\(\sum\limits_{i = 1}^k {{n_i}} {x_i} = 7960\) d’où \(\bar{x}= \frac{{7960}}{{50}} =\) 159,2 mm (voir graphe)
Remarque : La moyenne obtenue après regroupement des données en classe dans l’exemple de la longueur de la rectrice centrale diffère légèrement en raison d’une perte d’information. Si l’échantillonnage n’est pas de type aléatoire simple, les deux moyennes peuvent être très différentes.
5.1.2 La médiane
La médiane, \(M_e\), est la valeur du caractère pour laquelle la fréquence cumulée est égale à 0,5 ou 50%. Elle correspond donc au centre de la série statistique classée par ordre croissant, ou à la valeur pour laquelle 50% des valeurs observées sont supérieures et 50% sont inférieures.
- Dans le cas où les valeurs prises par le caractère étudié ne sont pas regroupées en classe,
- si \(n\) est impair, alors \(n = 2m + 1\) et la médiane est la valeur du milieu \(M_e = x_{m+1}\)
- si \(n\) est pair, alors \(n = 2m\) et une médiane est une valeur quelconque entre \(x_m\) et \(x_{m+1}\).
Dans ce cas il peut être commode de prendre le milieu.
- Dans le cas où les valeurs prises par le caractère étudié sont groupées en classe, on cherche la classe contenant le \({n^e}/2\) individu de l’échantillon. En supposant que tous les individus de cette classe sont uniformément répartis à l’intérieur, la position exacte du \({n^e}/2\) individu de la façon suivante par interpolation linéaire :
\({M_e} = {x_m} + ({x_{m + 1}} - {x_m})\left( {\frac{{\frac{n}{2} - {N_i}}}{{{n_i}}}} \right)\) (voir démonstration géométrique)
avec
\(x_m\): limite inférieure de la classe dans laquelle se trouve le \({n^e}/2\) individu (classe médiane).
\(x_{m + 1}\): limite supérieure de la classe dans laquelle se trouve le \({n^e}/2\) individu (classe médiane).
\(n_i\): effectif de la classe médiane
\(N_i\): effectif cumulé inférieur à \(x_m\)
\(n\) : taille de l’échantillon
Exemple :
Dans le cas de la distribution de la longueur de la rectrice centrale de la gélinotte huppée, la valeur de la médiane est :
- Cas des données non groupées :
\(n = 50\) donc \(M_e \in [x_25 , x_26 ]\)
soit \(M_e \in [158mm, 159mm]\) ou \(M_e =\) 158,5mm
- Cas des données groupées :
\(n=50\), la 25ème valeur se situe dans la classe [155-160[ qui contient les individus de 12 à 28.
d’où avec \(L_m=\) 155 mm, \(f_m=\) 17 individus, \(f_m\text{cum} =\) 11 individus et \(i\) = 5mm
\(M_e = 155 + \frac{5}{{17}}\left( {\frac{{50}}{2} - 11} \right)=\) 159,11 mm d’où \(M_e=\) 159,1 mm (voir graphe)
Remarque : La médiane ne s’applique qu’aux échelles ordinales, d’intervalles et de rapport, car elle nécessite un ordre linéaire entre les variables.
Si la distribution des valeurs est symétrique, la valeur de la médiane est proche de la valeur de la moyenne arithmétique.
\(M_e \approx \bar{x}\)
5.1.3 Le mode
Le mode, \(M_o\) d’une série statistique est la valeur du caractère la plus fréquente ou dominante dans l’échantillon. Le mode correspond à la classe de fréquence maximale dans la distribution des fréquences.
On peut identifier le mode comme la valeur médiane de la classe de fréquence maximale ou bien effectuer une interpolation linaire pour obtenir la valeur exacte du mode comme suit :
\({M_o} = {x_m} + \frac{{i\Delta i}}{{\Delta s + \Delta i}}\) (voir démonstration géométrique)
avec
\(x_m\): limite inférieure de la classe d’effectif maximal
\(i\) : intervalle de classe (\(x_{m+1} - x_m\))
\(\Delta i\): Ecart d’effectif entre la classe modale et la classe inférieure la plus proche
\(\Delta s\): Ecart d’effectif entre la classe modale et la classe supérieure la plus proche
Exemple :
Dans le cas de la distribution de la longueur de la rectrice centrale de la gélinotte huppée, la valeur du mode est :
- Valeur approchée :
La classe de fréquence maximale est [155,160[ avec \(n_i\) = 17 d’où \(M_o =\) 157,5 mm
- Valeur exacte :
\(M_o = 155 + \frac{{5 \times 8}}{( {1 * 8} )} =\) 159,44 mm d’où \(M_o =\) 159,4 mm (voir graphe)
avec \(x_m =\) 155 mm, \(\Delta i = 17-9 = 8\) , \(\Delta s = 17-16 = 1\) et \(i =\) 5mm
Remarque : Une distribution de fréquences peut présenter un seul mode (distribution unimodale) ou plusieurs modes (distribution bi ou trimodale).
Si la distribution des valeurs est symétrique, la valeur du mode est proche de la valeur de la moyenne arithmétique.
\(M_o \approx x\)
5.1.4 Comparaison des indicateurs de position

Exemples :
Représentation graphique des trois indices de position sur l’exemple de la distribution de la longueur de la rectrice centrale de la gélinotte huppée.
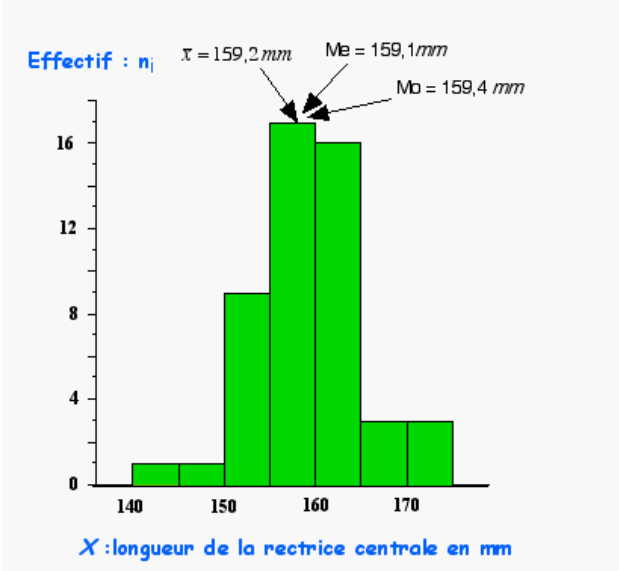
Dans le cas où le caractère étudié se distribue selon une loi normale Laplace-Gauss alors,
la moyenne \(\bar{x}\), la médiane \(M_e\) et le mode \(M_o\) prennent la même valeur.
Il existe d’autres paramètres de position comme la moyenne quadratique ou la moyenne géométrique qui ne seront pas développés dans ce cours.
5.2 Indicateurs de dispersion
Ces paramètres ont pour objectif dans le cas d’un caractère quantitatif de caractériser la variabilité des données dans l’échantillon.
Les indicateurs de dispersion fondamentaux sont la variance observée et l’écart-type observé.
5.2.1 La variance observée
Soit un échantillon de \(n\) valeurs observées \(x_1 , x_2 , ...., x_i ,...., x_n\) d’un caractère quantitatif \(X\) et soit \(\bar{x}\) sa moyenne observée. On définit la variance observée notée \(s^2\) comme la moyenne arithmétique des carrés des écarts à la moyenne.
\({s^2} = \frac{1}{n}\sum\limits_{i = 1}^n {({x_i} - \bar{x}}{)^2}\)
Pour des commodités de calcul, on se sert du théorème de Kœnig que nous démontrons dans un cas particulier.
Voici pourquoi :
Soit \(A = \sum\limits_{i = 1}^n {({x_i}} - \bar{x{)^2}}= \sum\limits_{i = 1}^n {(x_i^2 - 2{x_i}\bar{x}+ {{\bar{x}^2})}= \sum\limits_{i = 1}^n {x_i^2} } - \sum\limits_{i = 1}^n {2{x_i}} \bar{x}+ \sum\limits_{i = 1}^n {{{\bar{x}^2}}}\)
d’où \(A = \sum\limits_{i = 1}^{i = n} {x_i^2} - 2\bar{x\sum\limits_{i}= 1}^{i = n} {{x_i}} + n{\bar{x^2}}\) or \(\sum\limits_{i = 1}^{i = n} {{x_i}} = n\bar{x}\)
d’où \(A = \sum\limits_{i = 1}^{i = n} {x_i^2} - 2n{\bar{x^2}}+ n{\bar{x^2}}= \sum\limits_{i = 1}^{i = n} {x_i^2} - n{\bar{x^2}}\)
ainsi \(A = \sum\limits_{i = 1}^{i = n} {x_i^2} - n{\bar{x^2}}\)
La formule de la variance qui résulte du théorème de Kœnig est donc :
\(s_{}^2 = \frac{1}{n}\sum\limits_{i = 1}^{i = n} {x_i^2} - {\bar{x^2}}\)
Dans le cas de données regroupées en \(k\) classes d’effectif \(n_i\) (variable continue regroupée en classes ou variable discrète), la formule de la variance est la suivante :
\(s_{}^2 = \frac{1}{n}\sum\limits_{i = 1}^{i = k} {{n_i}({x_i}} - \bar{x{)^2}}\)
Pour des commodités de calcul, on utilisera la formule développée suivante :
\(s_{}^2 = \frac{1}{n}\sum\limits_{i = 1}^{i = k} {{n_i}x_i^2} - {\bar{x^2}}\) avec \(n = \sum\limits_{i = 1}^{i = k} {{n_i}}\)
L’écart-type observé correspond à la racine carrée de la variance observée:
\(s = \sqrt {{s^2}}\)
Exemple :
Dans le cas de l’étude du dimorphisme sexuel de la** gélinotte huppée,** la variance observée de la longueur de la rectrice centrale du mâle juvénile est :
- cas des données non groupées:
\(\sum\limits_{i = 1}^{i = n} {x_i^2} = 1\,263\,647\) et \(\bar{x} =\) 158,86 mm
\({s^2} = \frac{1}{50} ( 1263647 ) − {( 158,86 )^2} = 36,44\) d’où \(s^2 =\) 36,44 et \(s =\) 6,04 mm
- cas des données groupées :
\(\sum\limits_{i = 1}^{i = n} {{n_i}x_i^2} = 1\,269\,012,5\) et \(\bar{x} =\) 159,20 mm
\({s^2} = \frac{1}{50}( 1263647 ) − {( 158,86 )^2} = 35,61\) d’où \(s^2 =\) 35,61 et \(s=\) 5,97 mm
Remarque : De part sa définition, la variance est toujours un nombre positif. Sa dimension est le carré de celle de la variable. Il est toutefois difficile d’utiliser la variance comme mesure de dispersion car le recours au carré conduit à un changement d’unités. Elle n’a donc pas de sens biologique direct contrairement à l’écart-type qui s’exprime dans les mêmes unités que la moyenne.
5.2.2 Coefficient de variation
La variance et l’écart-type observée sont des paramètres de dispersion absolue qui mesurent la variation absolue des données indépendamment de l’ordre de grandeur des données.
Le coefficient de variation noté \(C.V.\) est un indice de dispersion relatif prenant en compte ce biais et est égal à :
\(C.V. = \frac{100s}{\bar{x}}\)
Exprimé en pour cent, il est indépendant du choix des unités de mesure permettant la comparaison des distributions de fréquence d’unité différente.
Exemple :
Le coefficient de variation des longueurs de la rectrice centrale des gélinottes huppées mâles juvéniles est égal à :
\(C.V. = \frac{100 \times 6,09}{158,86} = 3,83\%\)
6 Inférence aux lois de probabilité
Soit un caractère discret ou continu étudié sur \(n\) individus résultant d’un échantillonnage aléatoire simple d’une population, l’analyse des valeurs attribuées au caractère étudié va permettre d’établir le tableau des fréquences, la représentation graphique des données ainsi que le calcul des paramètres statistiques (moyenne arithmétique, variance observée, fréquence) (Statistique descriptive.
Différents critères vont permettre d’émettre des hypothèses qu’en à la loi de probabilité suivie par la variable aléatoire relative à ce caractère.

L’adéquation entre la distribution des valeurs observées avec l’échantillon et celles attendues avec la loi de probabilité inférée peut être testée par un test du \(c^2\) d’ajustement.