Chapitre 5/ Primitives – Intégration
Sandrine CHARLES
- Introduction
- 1 Primitives
- 2 La notion d’intégrale
- 3 Intégrales et inégalités
- 4 Méthodes de calcul exact d’intégrales
- 4.1 Utilisation des primitives usuelles
- 4.2 Intégration par décomposition en somme (linéarisation)
- 4.3 Changement de variable
- 4.4 Cas des fractions rationnelles
- 4.5 Cas simples de fonctions trigonométriques
- 4.6 Cas complexes de fonctions trigonométriques et hyperboliques
- 4.7 Intégrations par parties
- 4.8 Cas des fonctions de la forme \(P\left( x \right){e^{\alpha x}}\) avec \(P\left( x \right)\) polynôme
- 4.9 Compléments
- 5 Méthodes de calcul approché d’intégrales
- 6 Applications du calcul intégral
- 7 Exemples d’application en Biologie
Introduction
Ce chapitre repose sur les notions abordées aux chapitres 1 à 4, en particulier le chapitre 3 sur les dérivées. Le chapitre 5 revient sur la définition des primitives et intégrales, et donne toute une liste de « recettes » pour le calcul d’intégrales « non élémentaires ».
Le formulaire des primitives contient une liste des plus usuelles. Il est donc obligatoire de le connaître. Le contenu du chapitre 5 permet d’aborder des intégrales jugées au premier abord plus difficiles. Le programme de Deug SV correspond au premier niveau de lecture de ce cours. Pour ceux qui voudrait aller plus loin, vous trouverez au travers de nombreux liens, matière à vous satisfaire.
Un exemple en Biologie
Tout au long de ce chapitre, nous essaierons d’illustrer les différentes notions abordées, en traitant un exemple d’application en Médecine, dans lequel intervient la fonction suivante :
\[f\left( t \right) = 3{e^{ - 0.1t}}\]
\(f\) est définie sur l’intervalle \[\left[ {0;20} \right]\] et relie la quantité d’un certain médicament dans le sang après injection au temps \(t\), pendant une période de 20h qui suit l’injection.
Vers d’autres sites…
1 Primitives
Dans tout le chapitre 5, \(I\) désignera un intervalle fermé (ou segment) de \(\mathbb{R}\).
1.1 Définitions - Théorème fondamental
Définition (primitive sur un intervalle) :
Soit une fonction \(f:I \to \mathbb{R}\). On dit que \(F:I \to \mathbb{R}\) est une primitive de \(f\) sur \(I\) si \(F\) est dérivable sur \(I\), et si \(\forall x \in I\) \(F'\left( x \right) = f\left( x \right)\).
****Un exemple en Biologie****
Proposition (primitives d’une même fonction) :
Soit une fonction \(f:I \to \mathbb{R}\) admettant une primitive \(F\) sur \(I\). La fonction \(G:I \to \mathbb{R}\) est aussi une primitive de \(f\) sur \(I\) si et seulement si il existe une constante \(C \in \mathbb{R}\) telle que \(\forall x \in I\), \(G\left( x \right) = F\left( x \right) + C\).
Remarque : Une fonction ne peut pas avoir une seule primitive ; il est donc « interdit » de parler de la primitive d’une fonction.
Conséquence (primitive prenant une valeur donnée en un point) :
Soit une fonction \(f:I \to \mathbb{R}\) admettant une primitive \(F\) sur \(I\). Soient \({x_0} \in I\) et \({y_0} \in \mathbb{R}\).
Il n’existe qu’une seule primitive \(G\) de \(f\) telle que \(G\left( {{x_0}} \right) = {y_0}\) ; elle est donnée par \(G = F - F\left( {{x_0}} \right) + {y_0}\).
En particulier, \(H = F - F\left( {{x_0}} \right)\) est l’unique primitive de \(f\) sur \(I\) qui s’annule en \({x_0}\).
Remarque : La formule \(H = F - F\left( {{x_0}} \right)\) peut paraître troublante…en effet, \(H\) est une fonction bien définie et \(F\) est une quelconque des primitives de \(f\) : quel que soit le choix de \(F\), \(H\) reste inchangée.
****Un exemple en Biologie****
Théorème fondamental :
Si \(f:I \to \mathbb{R}\) est une fonction continue, alors elle admet une primitive (donc une infinité).
1.2 Primitives des fonctions usuelles
Le formulaire des primitives vous propose une liste de primitives des fonctions usuelles, qu’il est impératif de connaître par cœur.
ê Nous allons voir dans la suite que la plupart des théorèmes que nous avons démontré pour la dérivation (chapitre 3) fournissent des théorèmes sur les primitives.
1.3 Linéarité
Nous avons vu que si \(f\) et \(g\) sont dérivables sur \(I\), alors \(\forall \alpha ,\beta \in \mathbb{R}\) la fonction \(h = \alpha f + \beta g\) est dérivable sur \(I\) avec \(h' = \alpha f' + \beta g'\) (cf. chapitre 3, § 4.1).
Il en découle la proposition suivante :
Proposition :
Soient \(f\) et \(g\) deux fonctions définies sur un même intervalle \(I\) et admettant des primitives. Si \(F\) est une primitive de \(f\) et \(G\) une primitive de \(g\), alors, \(\forall \alpha ,\beta \in \mathbb{R}\), la fonction \(\alpha F + \beta G\) est une primitive sur \(I\) de la fonction \(\alpha f + \beta g\).
Cette proposition découle directement des propriétés de dérivation d’une somme de fonctions et du produit d’une réel par une fonction (Chapitre 3, § 4.1).
1.4 Fonctions composées
Nous avons également vu au chapitre 3 ( § 4.3) que si \(u\) est dérivable sur \(I\) et \(G\) dérivable sur \(J\), alors \(G \circ u\) est dérivable sur \(I\) et que \[\forall x \in I\], \({\left( {G\left( {u\left( x \right)} \right)} \right)^\prime } = u'\left( x \right)G'\left( {u\left( x \right)} \right)\).
La proposition suivante découle donc directement du théorème de dérivation des fonctions composées :
Proposition :
Soient \(u\) une fonction dérivable sur un intervalle \(I\), et \(g\) une fonction définie sur intervalle \(J\) tel que \(\forall x \in I\), \(u\left( x \right) \in J\).
Si \(g\) admet une primitive \(G\) sur \(J\), alors une primitive sur \(I\) de la fonction définie par \(f\left( x \right) = u'\left( x \right) \times g\left( {u\left( x \right)} \right)\) est la fonction \(F\) définie par \(F\left( x \right) = G\left( {u\left( x \right)} \right)\).
Ce théorème, appliqué lorsque \(g\) est une fonction usuelle, permet de rechercher les primitives de nombreuses fonctions \(f\) dérivables sur \(I\). Exemple 7.
2 La notion d’intégrale
2.1 Intégrale d’une fonction
Soit \(f:I \to \mathbb{R}\) une fonction admettant une primitive sur \(I\).
Soient \(F\) et \(G\) deux primitives de \(f\) sur \(I\). Alors, \(\forall x \in I\) \(G\left( x \right) = F\left( x \right) + C\) avec \(C \in \mathbb{R}\).
Ainsi, \(\forall a,b \in I\) \(G\left( b \right) - G\left( a \right) = F\left( b \right) + C - F\left( a \right) - C = F\left( b \right) - F\left( a \right)\).
Ce nombre est donc indépendant du choix de la primitive.
Définition 1 :
Soit \(f:I \to \mathbb{R}\) une fonction admettant une primitive sur \(I\) et \(F\) l’une d’entre elles.
Soient \(a,b \in I\). Alors le nombre \(F\left( b \right) - F\left( a \right)\) est appelé intégrale de \(f\) sur \(\left[ {a,b} \right]\).
Remarque : On peut remarquer que \(F\left( b \right) - F\left( a \right)\) ne dépend pas du choix de la primitive \(F\) parmi l’infinité des primitives de \(f\).
Interprétation géométrique
Considérons la fonction \(f\) définie sur \(\left[ {a,b} \right] = \left[ {1;3} \right]\) par \(f\left( x \right) = - {x^2} + 6x - 3\).
Voici la courbe représentative de \(f\) :
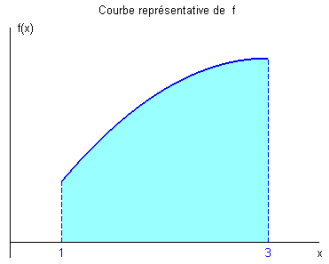
Unnamed Image
Désignons par \(A\) l’aire en bleu clair sous la courbe bleue.
Découpons l’intervalle \(\left[ {a,b} \right]\) en \(n\) intervalles plus petits de longueur \(\Delta x = \frac{{b - a}}{n}\) :
\(\begin{gathered}\)
{x_0} = a \$
{x_1} \$
{x_2} \$
\$
{x_i} \$
{x_{i + 1}} \$
\$
{x_n} = b \$
$\end{gathered} $ \(\forall i\) \({x_{i * 1}} - {x_i} = \Delta x\)
** ****(A) (B)**
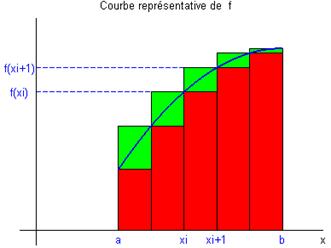
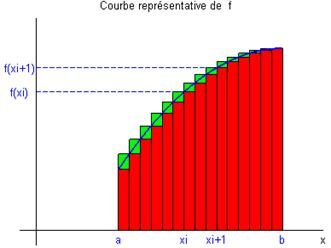
avec 5 intervalles entre a et b avec 15 intervalles entre a et b
· On désigne alors par \({A^ - }\) l’expression suivante :
${A^ - } = f( a )x + f( {{x_1}} )x + + f( {{x_i}} )x + + f( {{x_{n - 1}}} )x = {i * 0}^{n - 1} {f( {{x_i}} )( {{x{i + 1}} - {x_i}} )} $
- $ \({A^ - }\) représente alors la somme de tous les rectangles rouges
Il est clair que \({A^ - } < A\) et que \({A^ - }\) est d’autant plus proche de \(A\) que \(\Delta x\) est petit (Fig. A).
· On désigne alors par \({A^ + }\) l’expression suivante :
${A^ + } = f( {{x_1}} )x + + f( {{x_{i + 1}}} )x + + f( b )x = {i = 1}^n {f( {{x_i}} )( {{x{i + 1}} - {x_i}} )} $
- $ \({A^ + }\) représente alors la somme de tous les rectangles verts.
Il est clair que \({A^ + } > A\) et que \({A^ + }\) est d’autant plus proche de \(A\) que \(\Delta x\) est petit (Fig. B).
Par conséquent \({A^ - } < A < {A^ + }\) et on définit l’intégrale de \(f\) sur \(I\) par :
$A = {x 0} {A^ - } = {x 0} {A^ * } = _a^b {f( x )dx} $
Remarque
\(dx\) désigne un \(\Delta x\) infiniment petit : \(dx = \mathop {\lim }\limits_{{x_i} \to {x_{i + 1}}} \Delta x\)
Définition 2 (Intégrale et Aire) :
Soit \(f:\left[ {a,b} \right] \to \mathbb{R}\) une fonction positive admettant une primitive sur \(\left[ {a,b} \right]\) et (C) sa courbe représentative.
L’aire du domaine (A) délimitée par : * - la courbe (C) * - l’axe des abscisses * - les droites d’équations \(x = a\) et \(x = b\)
est $( {} ) = _a^b {f( x )dx} $, exprimée en unités d’aire (u.a.). Voir figure ci-dessous.
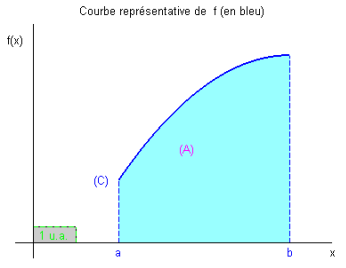 d’après Misset et al.
d’après Misset et al.
****Un exemple en Biologie****
Définition 3 :
Soit \(f:I \to \mathbb{R}\) une fonction admettant une primitive sur \(I\) et \(F\) l’une d’entre elles.
L’intégrale de \(f\) sur \[\left[ {a,b} \right]\] (définition 1) se note $_a^b {f( x )dx} $. Ainsi :
$F( b ) - F( a ) = _a^b {f( x )dx} $ que l’on note aussi \(\left[ {F\left( x \right)} \right]_a^b\)
$_a^b {f( x )dx} $ se lit « somme de \(a\) à \(b\) de \(f\left( x \right)dx\) ». *
Historiquement, on doit une telle définition à Riemann qui donna son nom aux sommes dites de Riemann $i {f( {{x_i}} )( {{x{i + 1}} - {x_i}} )} $. On parle alors d’intégrale de Riemann.
La façon dont nous venons de définir l’intégrale d’une fonction sur un intervalle revient à minorer ou à majorer l’intégrale par une somme de rectangles ; on parle de méthode des rectangles. Nous verrons ultérieurement d’autres méthodes d’approximation numérique des intégrales (chapitre 5, § 5).
Remarque : $_a^b {f( x )dx} $ est un nombre réel (voir définitions 1 et 2). Pour des raisons qui restent encore mystérieuses on dit que « l’on intègre \(f\) par rapport à la variable \(x\) sur l’intervalle \[\left[ {a,b} \right]\] ».
Bien évidemment, le symbole \(x\) n’a pas de rôle particulier (c’est une variable « muette ») et $_a^b {f( x )dx} $ représente la même quantité que $_a^b {f( t )dt} $ ou $_a^b {f( u )du} $.
Conséquences des définitions 1 et 3 :
\(\int\limits_a^a {f\left( x \right)dx} = 0\) \[\left[ {\int\limits_a^a {f\left( x \right)dx} = F\left( a \right) - F\left( a \right)} \right]\]
$_b^a {f( x )dx} = - _a^b {f( x )dx} $ \[\left[ {F\left( b \right) - F\left( a \right) = - \left( {F\left( a \right) - F\left( b \right)} \right)} \right]\]
****Un exemple en Biologie****
2.2 Intégrale et primitive
Définition 4 :
Soit une fonction \(f:I \to \mathbb{R}\) admettant des primitives sur \(I\).
On note $ $ l’ensemble des primitives de \(f\).
****Un exemple en Biologie****
Proposition :
Soient une fonction \(f:I \to \mathbb{R}\) admettant des primitives sur \(I\) et \({x_0} \in I\).
La fonction \(F\) définie sur \(I\) par l’intégrale $F( x ) = _{{x_0}}^x {f( * )dt} $ est l’unique primitive de \(f\) sur \(I\) qui s’annule en \({x_0}\).
2.3 Premières propriétés
2.3.1 Linéarité
Proposition :
Soient \(f\) et \(g\) deux fonctions continues sur \(\left[ {a,b} \right]\). \(\forall \alpha ,\beta \in \mathbb{R}\) :
$_a^b {( {f * g} )( x )dx} = _a^b {f( x )dx} + _a^b {g( x )dx} $
Remarque :
On dit que l’intégrale d’une somme est la somme des intégrales.
Exemple : \(\int\limits_0^1 {\left( {{x^2} - x} \right)dx} = \int\limits_0^1 {{x^2}dx} - \int\limits_0^1 {xdx} = \left[ {\frac{{{x^3}}}{3}} \right]_0^1 - \left[ {\frac{{{x^2}}}{2}} \right]_0^1 = - \frac{1}{6}\)
2.3.2 Signe de l’intégrale
Propositions :
- Soit \(f\) une fonction continue sur \(\left[ {a,b} \right]\).
Si \[\forall * \in \left[ {a,b} \right]\], \[f\left( x \right) \geqslant 0\] (resp. \[ \leqslant 0\]), alors \(\int\limits_a^b {f\left( x \right)dx} \geqslant 0\) (resp. \[ \leqslant 0\]).
- Soit \(f\) une fonction continue sur \(\left[ {a,b} \right]\). Si \(\forall x \in \left[ {a,b} \right]\), \(f\left( x \right) \leqslant g\left( x \right)\), alors :
$_a^b {f( x )dx} _a^b {g( x )dx} $
****Un exemple en Biologie****
Par extension, si \(f\), \(g\) et \(h\) sont trois fonctions intégrables sur \(\left[ {a,b} \right]\) telles que \(f \leqslant g \leqslant h\) sur \(\left[ {a,b} \right]\), alors $_a^b {f( x )dx} _a^b {g( x )dx} _a^b {h( x )dx} $.
Ainsi, si on ne connaît pas de primitive de la fonction \(g\), on peut malgré tout obtenir un encadrement de son intégrale sur \(\left[ {a,b} \right]\).
2.3.3 Relation de Chasles
Proposition :
Soit \(f\) une fonction continue sur \(\left[ {a,b} \right]\). Alors \(\forall * \in \left[ {a,b} \right]\) :
$_a^b {f( x )dx} = _a^c {f( x )dx} + _c^b {f( x )dx} $
Ce théorème découle immédiatement de la définition de l’intégrale. \(F\) étant une primitive de \(f\) sur \(\left[ {a,b} \right]\), pour tout \(c \in \left[ {a,b} \right]\), on a : \(F\left( c \right) - F\left( a \right) + F\left( b \right) - F\left( c \right) = F\left( b \right) - F\left( a \right)\).
Exemple : \(\int\limits_{ - {\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
\(\kern-\nulldelimiterspace} 2}}^{{\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
\(\kern-\nulldelimiterspace} 2}} {\cos xdx} = \int\limits_{ - {\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
\(\kern-\nulldelimiterspace} 2}}^0 {\cos xdx} + \int\limits_0^{{\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
$-} 2}} {xdx} $
****Un exemple en Biologie****
3 Intégrales et inégalités
3.1 Valeur moyenne d’une fonction sur un intervalle
Définition :
Soit \(f\) une fonction continue sur \(\left[ {a,b} \right]\) (\(a < b\)). On appelle valeur moyenne de \(f\) sur \(\left[ {a,b} \right]\), le réel $= _a^b {f( x )dx} $.
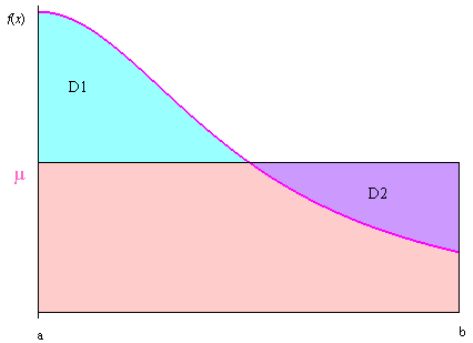
Interprétation graphique :
Dans le cas d’une fonction positive, la valeur moyenne d’une fonction est le réel µ tel que l’aire du rectangle de hauteur µ et de base (b-a) (rose + violet) soit égal à l’aire sous la courbe (rose + bleu).
Les aires des domaines D1 (bleu) et D2 (violet) sont identiques.
Unnamed Image
Théorème (théorème de la moyenne) :
Soit \(f\) une fonction continue sur \(\left[ {a,b} \right]\) (\(a < b\)). Il existe \(c \in \left[ {a,b} \right]\) tel que : * \(\int\limits_a^b {f\left( x \right)dx} = \left( {b - a} \right)f'\left( c \right)\)
3.2 Inégalités de la moyenne
Propositions :
Soit \(f\) une fonction admettant des primitives sur \(\left[ {a,b} \right]\).
Si \(m \leqslant f \leqslant M\), alors \(m\left( {b - a} \right) \leqslant \int\limits_a^b {f\left( x \right)dx} \leqslant M\left( {b - a} \right)\).
Si \(\left| f \right| \leqslant M\), alors \(\left| {\int\limits_a^b {f\left( x \right)dx} } \right| \leqslant M\left| {b - a} \right|\).
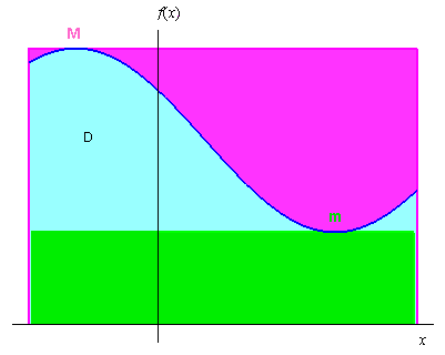
Interprétation graphique :
Voir figure ci-dessous
Dans le cas d’une fonction positive sur \(\left[ {a,b} \right]\) et \(m > 0\), l’inégalité de la moyenne (i) traduit le fait que l’aire du domaine D ( + * comprise entre l’aire du rectangle de hauteur \(m\) et de base (b – a) ( ), et l’aire du rectangle de hauteur \(M\) et de même base ( ).
Unnamed Image
Remarque :
L’inégalité de la moyenne (i) correspond en fait à l’inégalité des accroissements finis appliquée à l’intégrale fonction de sa borne supérieure, définie par $F( x ) = _{{x_0}}^x {f( x )dx} $.
3.3 Valeur absolue d’une intégrale
Proposition :
Soit \(f\) une fonction continue sur \(\left[ {a,b} \right]\). On a alors :
$| {_a^b {f( x )dx} } | _a^b {| {f( x )} |dx} $.
4 Méthodes de calcul exact d’intégrales
4.1 Utilisation des primitives usuelles
Le plus souvent le calcul d’une intégrale se ramène à la recherche d’une primitive.
Ainsi, le calcul de $_a^b {f( x )dx} $ revient généralement à justifier l’existence d’une primitive \(F\) de \(f\) sur \(\left[ {a,b} \right]\), puis à calculer \(F\) à l’aide du tableau des primitives usuelles ; on a alors immédiatement \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\).
Exemple 14 : Calculer \(\int\limits_{ - 1}^2 {x{e^{{{{x^2}} \mathord{\left/\)
\({\vphantom {{{x^2}} 2}} \right.\)
$-} 2}}}dx} $. Réponse.
4.2 Intégration par décomposition en somme (linéarisation)
On a vu précédemment (Chapitre 5, § 2.3.1) que :
$_a^b {( {f + g} )( x )dx} = _a^b {f( x )dx} + _a^b {g( x )dx} $
Par généralisation, on obtient aisément que :
$a^b {( {{k = 1}^n {{k}{f_k}( x )} } )dx} = {k = 1}^n {{_k}_a^b {{f_k}( x )dx} } $
Exemple d’utilisation 15 : Calculer $_1^2 {( {x - } )dx} $. Réponse.
4.3 Changement de variable
4.3.1 Cas général des intégrales
Théorème :
Soient \(\phi :\left[ {a,b} \right] \to \mathbb{R}\) une fonction de classe \({C^1}\) (continue et telle que ) strictement monotone et \(f:\left[ {\phi \left( a \right),\phi \left( b \right)} \right] \to \mathbb{R}\) une fonction continue sur \(\left[ {\phi \left( a \right),\phi \left( b \right)} \right]\). Alors :
$_{( a )}^{( b )} {f( x )dx} = _a^b {( {f } )( t )’( t )dt} $
avec \[x = \phi \left( t \right)\] et \[dx = \phi '\left( t \right)dt\].
Remarque 1 :
Dans le théorème précédent, on a \[\phi \left( {\left[ {a,b} \right]} \right) = \left[ {\phi \left( a \right),\phi \left( b \right)} \right]\], c’est-à-dire que \[\phi \] est bijective de \(\left[ {a,b} \right]\) sur \(\left[ {\phi \left( a \right),\phi \left( b \right)} \right]\).
Remarque 2 :
Si \(F\) est une primitive de \(f\), alors on peut écrire :
\(\int\limits_a^b {\left( {f \circ \phi } \right)\left( t \right)\phi '\left( t \right)dt} = \left[ {\left( {F \circ \phi } \right)\left( t \right)} \right]_a^b = F\left( {\phi \left( b \right)} \right) - F\left( {\phi \left( a \right)} \right)\)
Cas particuliers :
\(\int\limits_a^b {{e^{\phi \left( t \right)}}\phi '\left( t \right)dt} = \left[ {{e^{\phi \left( t \right)}}} \right]_a^b\)
\(\int\limits_a^b {\frac{{\phi '\left( t \right)}}{{\phi \left( t \right)}}dt} = \left[ {\ln \left| {\phi \left( t \right)} \right|} \right]_a^b\)
\(\int\limits_a^b {{\phi ^n}\left( t \right)\phi '\left( t \right)dt} = \left[ {\frac{{{\phi ^{n * 1}}\left( t \right)}}{{n + 1}}} \right]_a^b\)
Exemple : Calculer $_0^1 { dx} $. Réponse
4.3.2 Application au calcul des primitives
Théorème :
Soient* *$$ une fonction bijective de classe \({C^1}\) de \(J\) sur \(I\) et \(f\) une fonction continue sur \(I\).
Si \[F\left( x \right) = \int {f\left( x \right)dx} \] (\(F\) est une primitive de \(f\)), alors :
$F= $ *
Autre formulation :
Si \(G\) est une primitive de \[\left( {f \circ \phi } \right)\phi '\] sur \(J\), alors \[G \circ \phi \] est une primitive de \(f\) sur I :
$G( x ) = $ avec \[x = \phi \left( t \right)\] et \[dx = \phi '\left( t \right)dt\]
Il vient $G( {( t )} ) = $
4.3.4 Conséquences
Si \(\int {f\left( x \right)dx} = F\left( x \right) + C\), alors \(\int {f\left( {\alpha x} \right)dx} = \frac{{F\left( {\alpha x} \right)}}{\alpha } + C\) avec \(\alpha \ne 0\)
\(f\) paire $ $ $_{ - a}^a {f( x )dx} = 2_0^a {f( x )dx} $
\(f\) impaire $ $ \(\int\limits_{ - a}^a {f\left( x \right)dx} = 0\)
\(\int\limits_0^{{\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
\(\kern-\nulldelimiterspace} 2}} {f\left( {\sin x,\cos x} \right)dx} = \int\limits_0^{{\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
$-} 2}} {f( {t,t} )dt} $.
En effet, le remplacement de \[\sin x\] par \[\cos x\] ne change pas l’intégrale entre 0 et \(${\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
\(\kern-\nulldelimiterspace} 2}\)$ d’une fonction de \[\sin x\] et \[\cos x\]. Le changement de variable correspondant est \($x = {\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
\(\kern-\nulldelimiterspace} 2} - t\)$.
En particulier, \($\int\limits_0^{{\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
\(\kern-\nulldelimiterspace} 2}} {{{\sin }^n}xdx} = \int\limits_0^{{\pi \mathord{\left/\)
\({\vphantom {\pi 2}} \right.\)
$-} 2}} {{{}^n}tdt} $$.
- \(f\) \(T\)-périodique $ $ $_a^{a + T} {f( x )dx} = 0^T {f( x )dx} $ ou bien encore ${a + T}^{b + T} {f( x )dx} * _a^b {f( x )dx} $
Exemples 21
- \[\int\limits_{ - 1}^1 {\left( {{x^4} + {x^2} - 1} \right)dx} = 2\int\limits_0^1 {\left( {{x^4} + {x^2} - 1} \right)dx} = 2\left[ {\frac{{{x^5}}}{5} + \frac{{{x^3}}}{3} - x} \right]_0^1 = - \frac{{14}}{{15}}\]
\((2)\)\(\int\limits_{{\pi \mathord{\left/\)
\((3)\)${} .
\((4)\)\(\kern-\nulldelimiterspace} 2}}^{{{3\pi } \mathord{\left/\)
\((5)\)${} .
\((6)\)\(\kern-\nulldelimiterspace} 2}} {\sin \left( {2x} \right)dx} \underbrace = _{{\text{avec }}a = {\pi \mathord{\left/\)
\((7)\)\({\vphantom {\pi 2}} \right.\)
- \(\kern-\nulldelimiterspace} 2}}\int\limits_0^\pi {\sin \left( {2x} \right)dx} = \left[ {\frac{1}{2}\cos \left( {2x} \right)} \right]_0^\pi * 0\) ;
La fonction \[\sin \left( {2x} \right)\] est \[\pi \]-périodique.
4.4 Cas des fractions rationnelles
Définition :
Une fraction rationnelle se présente sous la forme \(\frac{{P\left( * \right)}}{{Q\left( x \right)}}\) où \(P\left( * \right)\) et \(Q\left( x \right)\) sont des polynômes à coefficients dans \(\mathbb{R}\) (ou \(\mathbb{C}\)).
Sauf cas particuliers (qui confirment que la première méthode à essayer doit toujours être le changement de variable), par exemple :
\[\int {\frac{{3{x^2} + 2x - 1}}{{{x^3} + {x^2} - x}}dx} = \int {\frac{{u'}}{u}} dx = \ln \left| {{x^3} + {x^2} - x} \right| + C\]
l’intégration des fractions rationnelles nécessite la décomposition de la fraction en éléments simples. Cette dernière repose sur la connaissance des racines des polynômes \(P\) et* Q*.
4.4.1 Décomposition en éléments simples
Ø Si \(d^\circ \left( Q \right) \leqslant d^\circ \left( P \right)\), on peut effectuer la division euclidienne de \(P\left( x \right)\) par \(Q\left( x \right)\) suivant les puissances décroissantes pour faire apparaître une partie entière, qui est un polynôme en \(x\), et une nouvelle fraction rationnelle \(\frac{{{P_1}\left( x \right)}}{{Q\left( x \right)}}\) où \(d^\circ \left( Q \right) \geqslant d^\circ \left( {{P_1}} \right)\).
On effectue dans ce cas une décomposition en éléments simples de \(\frac{{{P_1}\left( * \right)}}{{Q\left( x \right)}}\).
Ø Si \(d^\circ \left( Q \right) \geqslant d^\circ \left( P \right)\), et \({\alpha _i}\) étant l’ordre de multiplicité de la racine réelle \({x_i}\), \({\beta _i}\) celui des deux racines complexes conjuguées de \({x^2} + {p_i}x + {q_i} = 0\) avec \(p_i^2 - 4{q_i} < 0\), alors :
$ = + $ avec \(1 \leqslant {\gamma _i} \leqslant {\alpha _i}\) et \(1 \leqslant {\delta _i} \leqslant {\beta _i}\) * Les sommes sont prises pour chacune des racines réelles et des couples de racines complexes conjuguées.
Cette décomposition s’appelle la décomposition en éléments simples de \(\frac{{P\left( x \right)}}{{Q\left( x \right)}}\).
Exemple 22 : Décomposer en éléments simples \(\frac{{P\left( * \right)}}{{Q\left( x \right)}} = \frac{1}{{{x^4} - x}}\). Réponse
4.4.2 Intégration d’un élément simple de la forme** **\[\int {\frac{{dx}}{{{{\left( {x - {x_0}} \right)}^\gamma }}}} \]
Il s’agit de calculer \[\int {\frac{{dx}}{{{{\left( {x - {x_0}} \right)}^\gamma }}}} \] pour \[\gamma \] entier \[ \geqslant 1\].
Deux cas peuvent se présenter :
\[\gamma = 1\] : \[\int {\frac{{dx}}{{\left( {x - {x_0}} \right)}}} = \ln \left| {x - {x_0}} \right| + C\]
\[\gamma \ne 1\] : \[\int {\frac{{dx}}{{{{\left( {x - {x_0}} \right)}^\gamma }}}} = \int {{{\left( {x - {x_0}} \right)}^{ - \gamma }}dx} = \frac{{{{\left( {x - {x_0}} \right)}^{1 - \gamma }}}}{{1 - \gamma }} + C\]
Exemple 23 : Calculer $ $. Réponse
4.4.3 Intégration d’un élément simple de la forme \[\frac{{Ax + B}}{{{{\left( {{x^2} + px + q} \right)}^\delta }}}\]
Il s’agit de calculer \[F\left( * \right) = \int {\frac{{Ax + B}}{{{{\left( {{x^2} + px + q} \right)}^\delta }}}dx} \] pour \[\delta \] entier \[ \geqslant 1\], avec \[{p^2} - 4q < 0\].
Le mieux est de procéder selon les quatre étapes suivantes :
S’armer de patience… !
Faire apparaître dans \[Ax + B\] la dérivée de \[{x^2} + px + q\] :
\[Ax * B = \frac{A}{2}\left( {2x + p} \right) + B - \frac{{Ap}}{2}\]
Ainsi, \[F\left( x \right) = \frac{A}{2}\int {\frac{{2x + p}}{{{{\left( {{x^2} + px + q} \right)}^\delta }}}dx} + \left( {B - \frac{{Ap}}{2}} \right)\int {\frac{{dx}}{{{{\left( {{x^2} + px + q} \right)}^\delta }}}} \]
C’est-à-dire \[F\left( x \right) = \frac{A}{2}\int {\frac{{du}}{{{u^\delta }}}} + \lambda \int {\frac{{dx}}{{{{\left( {{x^2} + px * q} \right)}^\delta }}}} \]
\[\int {\frac{{du}}{{{u^\delta }}}} \] est l’intégrale d’un élément simple de la forme précédente (voir § 4.4.2).
Reste donc à calculer \[\int {\frac{{dx}}{{{{\left( {{x^2} + px + q} \right)}^\delta }}}} \]
- Décomposer \[{x^2} + px + q\] en une somme de carrés :
\[{x^2} * px + q = {\left( {x + \frac{p}{2}} \right)^2} + q - \frac{{{p^2}}}{4} = {t^2} * {k^2}\] où \[t = x + \frac{p}{2}\] et \[k = \sqrt {q - \frac{{{p^2}}}{4}} > 0\] (\[{p^2} - 4q < 0\])
\[\int {\frac{{dx}}{{{{\left( {{x^2} + px + q} \right)}^\delta }}}} = \int {\frac{{dt}}{{{{\left( {{t^2} + {k^2}} \right)}^\delta }}}} \]
- Calculer \[\int {\frac{{dt}}{{{{\left( {{t^2} + {k^2}} \right)}^\delta }}}} \]
Si \[\delta = 1\], alors \[\int {\frac{{dt}}{{{t^2} + {k^2}}}} = \frac{1}{k}\arctan \left( {\frac{t}{k}} \right)\]
Si \[\delta \ne 1\], alors on pose \[\tan u = \frac{t}{k}\] soit \[u = \arctan \left( {\frac{t}{k}} \right)\]. Ainsi, on obtient :
\[\int {\frac{{dt}}{{{{\left( {{t^2} + {k^2}} \right)}^\delta }}}} = {k^{1 - 2\delta }}\int {\frac{{\left( {1 + {{\tan }^2}u} \right)}}{{{{\left( {1 + {{\tan }^2}u} \right)}^\delta }}}du} = {k^{1 - 2\delta }}\int {{{\cos }^{2\delta - 2}}udu} \]
\[\int {{{\cos }^{2\delta - 2}}udu} \] s’obtient par linéarisation et/ou changement de variable (§ 4.3.).
- Rassembler tous les résultats intermédiaires précédents pour calculer \[F\left( x \right)\].
Exemple 24 : Calculer \[\int {\frac{{x + 2}}{{{x^2} + x + 1}}dx} \]. Réponse
Exemple 26 : Calculer \[I = \int\limits_0^1 {\frac{{dx}}{{x + \sqrt {1 - x} }}} \]. Réponse
4.5 Cas simples de fonctions trigonométriques
Soit \(f\) une fonction trigonométrique de la forme \(f\left( x \right) = {\sin ^p}x{\cos ^q}x\). Le changement de variable qui doit être utilisé va dépendre de la parité de \(p\), \(q\).
On cherche à calculer : \[F\left( x \right) = \int {{{\sin }^p}x{{\cos }^q}xdx} \]
Cas n°1 : \(q\) est impair On pose \[t = \sin x\]
\[F\left( x \right) = \int {{{\sin }^p}x{{\cos }^q}xdx} = \int {{{\sin }^p}x{{\cos }^{q - 1}}x\cos xdx} * \pm \int {{t^p}{{\left( {1 - {t^2}} \right)}^{\frac{{q - 1}}{2}}}dt} \] \($\left\{ \begin{gathered}\)
\($+ \quad {\text{si }}\cos x > 0 \hfill \\\)
- x < 0 \$
\(\end{gathered} \right.\)$
Exemple : \[\int {{{\cos }^5}xdx} = \int {{{\left( {1 - {t^2}} \right)}^2}dt} = t - \frac{{2{t^3}}}{3} + \frac{{{t^5}}}{5} + C = \sin * - \frac{{2{{\sin }^3}x}}{3} + \frac{{{{\sin }^5}x}}{5} + C\]
Cas n°2 : \(p\) est impair On pose \[t = \cos x\]
\[ \Rightarrow \] même principe que dans le cas n°1.
Exemple : \[\int {{{\sin }^3}x{{\cos }^4}xdx} = \int {\left( {{t^2} - 1} \right){t^4}dt} = \frac{{{t^7}}}{7} - \frac{{{t^5}}}{5} + C = \frac{{{{\cos }^7}x}}{7} - \frac{{{{\cos }^5}x}}{5} + C\]
Cas n°3 : \(p\) et \(q\) sont pairs et positifs On diminue le degré en utilisant les formules :
\({\sin ^2}x = \frac{{1 - \cos 2x}}{2}\) et \({\cos ^2}x = \frac{{1 + \cos 2x}}{2}\)
On recommence alors comme précédemment avec \[{\sin ^r}2x\] et \[{\cos ^s}2x\].
Exemple : \[\int {{{\cos }^4}xdx} = \frac{1}{8}\int {\left( {\cos 4x + 4\cos 2x + 3} \right)dt} = \frac{{\sin 4x}}{{32}} + \frac{{\sin 2x}}{4} + \frac{{3x}}{8} + C\]
Cas n°4 : \(p\) et \(q\) sont pairs (ou impairs), l’un au moins étant négatif On pose \[t = \tan x\]
Ê Calculer \[{I_1} = \int {\frac{{{{\cos }^3}x}}{{{{\sin }^4}x}}} dx\] Réponse
4.7 Intégrations par parties
Si l’intégrale cherchée ne peut pas être obtenue par utilisation d’une primitive usuelle, il peut être commode de la transformer en une ou plusieurs autres intégrales que l’on sait calculer.
****Cette méthode n’est à utiliser que si toutes les autres méthodes ont échoué.****
4.7.1 Intégration par parties
Proposition :
Soient \(u\left( x \right)\) et \(v\left( x \right)\) deux fonctions dérivables sur un même intervalle \(\left[ {a,b} \right]\) et \(f\) une fonction continue sur \(\left[ {a,b} \right]\) telle que \(f\left( x \right) = u\left( x \right)v'\left( x \right)\). Alors :
$_a^b {f( x )dx} = _a^b {u( x )v’( x )dx} = _a^b - _a^b {u’( x )v( x )dx} $
Remarque :
Cette technique permet dans la pratique d’intégrer ou de simplifier certaines intégrales où \(f\left( x \right)\) est le produit d’une fonction \(u\) de dérivée simple et d’une fonction \(w\) facile à intégrer ; dans ce cas, on prendra \(v' = w\).
Exemple 16 : Calculer $_0^1 {dx} $. Réponse.
Exemples 17
Ê Calculer $_1^2 {{x^2}xdx} $ Réponse
Ë Calculer $_0^ $ Réponse
4.7.2 Intégration par parties successives
Proposition :
Soient \(u\left( x \right)\) et \(v\left( x \right)\) deux fonctions de classe \({C^n}\) sur un même intervalle \(\left[ {a,b} \right]\). On a alors l’égalité suivante :
$_a^b {u( x ){v^{( n )}}( x )dx} = [ {_{k = 0}^{n - 1} {{{( { - 1} )}k}{u{( k )}}( x ){v^{( {n - k} )}}( x )} } ]_a^b + {( { * 1} )^n}_a^b {{u^{( n )}}( x )v( x )dx} $
· Si \(n = 2\), alors $_a^b {u( x )v’’( x )dx} = _a^b + _a^b {u’’( x )v( x )dx} $
· Si \(n = 3\), alors $_a^b {u( x )v’’’( x )dx} = _a^b - _a^b {u’’’( x )v( x )dx} $
La démonstration de cette proposition se fait par récurrence.
Exemple 18
Calculer $I = _{ * 1}^0 {{x^2} dx} $ par deux intégrations successives puis en appliquant l’égalité de la proposition précédente. Vérifier que les résultats sont identiques. Réponse
4.8 Cas des fonctions de la forme \(P\left( x \right){e^{\alpha x}}\) avec \(P\left( x \right)\) polynôme
On cherche ici à calculer $F( * ) = $
Lorsque le degré de \(P\) est petit, on peut utiliser des intégrations par parties successives (en nombre égal au degré de \(P\)), en posant \[u\left( x \right) = P\left( x \right)\].
Par contre, si le degré de \(P\) est élevé, il est recommandé d’utiliser une méthode de coefficients indéterminés, c’est-à-dire que l’on cherche \(F\left( x \right) = Q\left( * \right){e^{\alpha x}}\) avec \[\deg Q = \deg P\].
Exemple 29 : Calculer \[I = \int {\left( {{x^3} - 2x + 1} \right){e^{ - x}}dx} \] Réponse
4.9 Compléments
5 Méthodes de calcul approché d’intégrales
Lorsque la primitive de \[f\left( * \right)\] ne peut pas être calculée de façon simple, ou que cela demande des calculs trop longs, on est alors amené à calculer \[\int\limits_a^b {f\left( x \right)dx} \] de manière approchée à l’aide d’une méthode numérique.
Nous présentons dans ce paragraphe les méthodes graphiques les plus classiques.
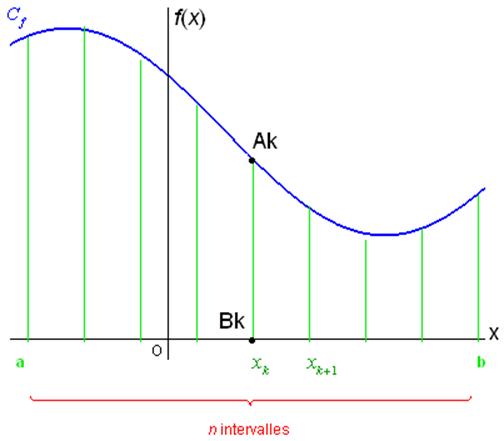
Soit \(f\) une fonction positive et intégrable sur un intervalle \[\left[ {a,b} \right]\] et \[\frac{{{x_k} + {x_{k + 1}}}}{2}\] sa courbe représentative ; On cherche une valeur approchée de \[\int\limits_a^b {f\left( x \right)dx} \].
L’idée de départ, commune aux méthodes graphiques qui vont nous intéresser, est que l’on partage l’intervalle d’intégration \[\left[ {a,b} \right]\] en \(n\) intervalles égaux \[\left[ {{x_k};{x_{k + 1}}} \right]\]de longueur \[h = \frac{{b - a}}{n}\], avec \[{x_0} = a\] et \[{x_n} = b\].
Unnamed Image
Les points \[{A_k}\] ont pour coordonnées \[\left( {{x_k},f\left( {{x_k}} \right)} \right)\] ;
Les points \[{B_k}\] ont pour coordonnées \[\left( {{x_k},0} \right)\].
On désigne par \[{g_k}\] une approximation de la fonction \(f\) sur les intervalles \[\left[ {{x_k};{x_{k + 1}}} \right]\].
Ainsi, on peut décomposer \[\int\limits_a^b {f\left( x \right)dx} \] en \[\sum\limits_{k * 0}^{n - 1} {{I_k}} \] avec \[{I_k} = \int\limits_{{x_k}}^{{x_{k + 1}}} {f\left( x \right)dx} \]. On prend alors comme valeur approchée de \[{I_k}\] : \[{J_k} = \int\limits_{{x_k}}^{{x_{k + 1}}} {{g_k}\left( x \right)dx} \].
Le choix de la fonction \[{g_k}\] conduit à l’une des trois méthodes présentées ci-dessous.
5.1 Méthode des rectangles
Cette méthode est directement inspirée de la définition des intégrales.
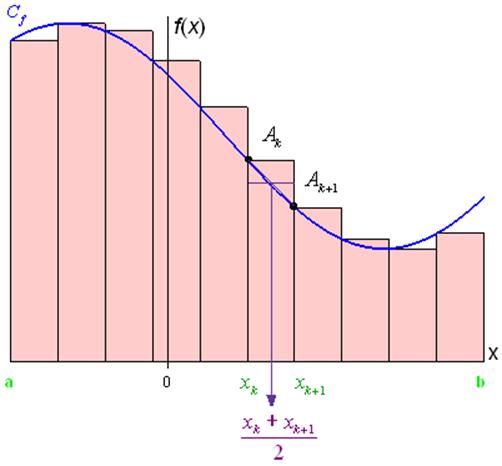
On prend comme fonction \[{g_k}\], la fonction constante \[f\left( {\frac{{{x_k} + {x_{k + 1}}}}{2}} \right)\] qui correspond à la valeur de \(f\) au point milieu de l’intervalle \[\left[ {{x_k};{x_{k + 1}}} \right]\].
Ainsi, on a \[{J_k} = f\left( {\frac{{{x_k} + {x_{k + 1}}}}{2}} \right)\int\limits_{{x_k}}^{{x_{k + 1}}} {dx} * f\left( {\frac{{{x_k} + {x_{k + 1}}}}{2}} \right)\left( {{x_{k + 1}} - {x_k}} \right) = hf\left( {\frac{{{x_k} + {x_{k + 1}}}}{2}} \right)\].
La valeur approchée de \(I\) est alors donnée par (voir figure ci-dessous) :
\[I \simeq J = \frac{{b - a}}{n}\sum\limits_{k = 0}^{n - 1} {f\left( {\frac{{{x_k} + {x_{k + 1}}}}{2}} \right)} \]
Unnamed Image
Remarque : cette méthode avait déjà été présentée sous un autre point de vue au début de ce chapitre 5 (§ 2.1).
5.2 Méthode des trapèzes
On prend comme fonction \[{g_k}\], la fonction affine égale à \(f\) aux points extrêmes de l’intervalle \[\left[ {{x_k};{x_{k + 1}}} \right]\] ; graphiquement, cela revient à considérer des trapèzes au lieu des rectangles de la figure précédente. \[{J_k}\] est alors égale à l’aire du trapèze \[{A_k}{B_k}{B_{k + 1}}{A_{k + 1}}\].
Ainsi \[{J_k} = \frac{h}{2}\left[ {f\left( {{x_k}} \right) + f\left( {{x_{k + 1}}} \right)} \right]\], ce qui conduit à l’approximation suivante :
\[I \simeq J = \frac{{b - a}}{{2n}}\left[ {f\left( a \right) + 2\sum\limits_{k = 1}^{n - 1} {f\left( {{x_k}} \right)} + f\left( b \right)} \right]\]
5.3 Autres méthodes
Il existe de nombreuses autres méthodes : méthode du point milieu, méthode de Simpson…
6 Applications du calcul intégral
Une des applications est celle du calcul de l’aire d’un domaine.
Prenons un exemple : on cherche à calculer l’aire du domaine \(D\) défini par :
\[D = \left\{ {\left( {x,y} \right) \in {\mathbb{R}^2}/0 \leqslant x \leqslant 1{\text{ et }}{x^2} \leqslant y \leqslant x} \right\}\]
Dessinons d’abord le domaine \(D\).
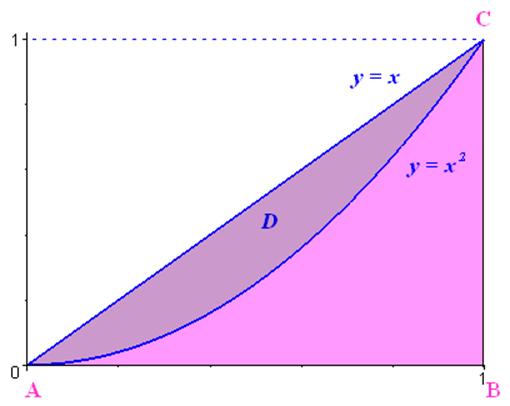
Unnamed Image
L’aire du domaine \(D\) correspond à la différence entre l’aire du triangle ABC * + ) et l’aire sous la courbe de \[{x^2}\] ( ) :
\[A = {I_1} - {I_2}\]
\[A = \int\limits_0^1 {xdx} - \int\limits_0^1 {{x^2}dx} \]
\[A = \left[ {\frac{{{x^2}}}{2}} \right]_0^1 - \left[ {\frac{{{x^3}}}{3}} \right]_0^1\]
\[A = \frac{1}{2} - \frac{1}{3} = \frac{1}{6}\;u.a.\]
7 Exemples d’application en Biologie
7.1 Un exemple en Démographie
L’évolution de la taille de la population du Botswana ces 25 dernières années est représentée à l’aide des données ci-dessous : * align=center>
Temps (année)
Nombre d’habitants (millions)
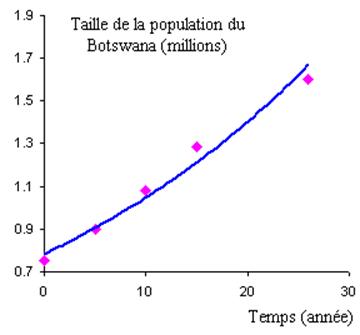
Unnamed Image
1975
0.755
1980
0.901
1985
1.078
1990
1.285
1.6 * *
La fonction exponentielle permet de décrire cette évolution et l’on obtient la relation suivante :
\[P = 0.7835{e^{0.0291t}}\]
Si on désigne par \(P\) la taille de la population du Botswana et par \(t\) l’année (\[t = 0\] correspondant à 1975).
On peut ainsi calculer le temps de doublement de la population, c’est-à-dire la valeur \[\theta \] de t telle que \[P\left( {t + \theta } \right) = 2P\left( t \right)\] :
\($\begin{gathered}\)
P( {t * } ) = 2P( t ) \$
\$
0.7835{e^{0.0291( {t + } )}} = 2 0.7835{e^{0.0291t}} \$
\$
{e^{0.0291}} = 2 \$
\$
24{} \$
$\end{gathered} $$
Supposons qu’en 2001, certains habitants craignent cette augmentation massive de la population prévue d’ici 25 ans ; en effet, selon l’équation précédente, la taille de la population aura doublé par rapport à celle de 2001 en 2025 pour passer à 3.2 millions d’habitants. On peut raisonnablement imaginer que ces habitants vont alors chercher à émigrer vers d’autres pays.
L’intégrale du taux d’émigration sur 25 ans est égal à l’émigration totale pendant cette période.
Si on suppose qu’un quart de la population de 2001 (soit 0.4 millions d’habitants) va émigrer ces 25 prochaines années, et si on suppose que le taux d’émigration \(a\) va augmenter de façon linéaire pendant cette période, il vient :
\[\int\limits_0^{25} {atdt = \frac{{1.6}}{4}} \]
Nous en déduisons que le taux d’émigration*** a*** est égal à : \[a = 0.{\text{0128}}\], exprimé en millions d’habitants par an.
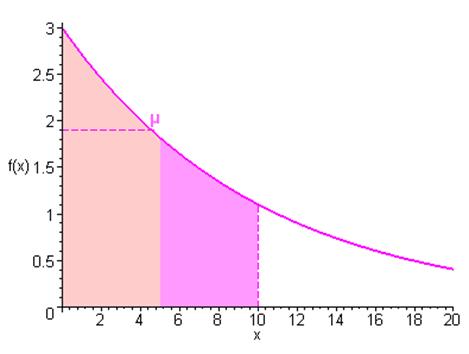
7.2 Un exemple en Médecine
Considérons la fonction \(f\) définie sur \[\left[ {0;20} \right]\] par :
\[f\left( t \right) = 3{e^{ - 0.1t}}\]
\(f\) relie la quantité d’un certain médicament dans le sang au temps \(t\), pendant les 20h qui suivent l’injection.
Unnamed Image
On peut calculer la quantité moyenne de médicament présente dans le sang pendant les 10 premières heures :
\[\mu = \frac{1}{{10}}\int\limits_0^{10} {f\left( t \right)dt} = 3\left( {1 - {e^{ - 1}}} \right) \simeq {\text{1}}{\text{.8964}}\;\,{\text{u}}\].