Chapitre 4 — Lois de Probabilité

2.1.1 Définition

Exemple :

La distribution des chiffres obtenus au lancer de dé (si ce dernier est non pipé) suit une loi uniforme dont la loi de probabilité est la suivante :

avec pour espérance : \(E(X) = \frac{1}{6}\sum\limits_{i = 1}^6 i = 3,5\) et pour variance \(V(X) = \frac{1}{6}\sum\limits_{i = 1}^6 {i^2 - E{(X)}^2} = 2,92\)

où les valeurs \({x_i}\) correspondent au rang \(i\) de la variable \(X\) dans la série.

2.1.2 Espérance et variance

2.2.1 Définition

Soit un univers \(\Omega\) constitué de deux éventualités, \(S\) pour succès et \(E\) pour échec

\(Ω = \{ E , S \}\)

sur lequel on construit une variable aléatoire discrète, « nombre de succès » telle que au cours d’une épreuve,

si \(S\) est réalisé, \(X = 1\)

si \(E\) est réalisé, \(X = 0\)

2.2.2 Espérance et variance

L’espérance de la variable de Bernoulli est

\(E(X) = p\)

car par définition \(E(X) = \sum\limits_{i = 1}^2 {x_i} {p_i} = (0 \times q) + (1 \times p) = p\)

La variance de la variable de Bernoulli est

\(V(X) = pq\)

car par définition

\(V(X) = \sum\limits_{i = 1}^2 {x_i^2} {p_i} - E(X)^2 = [(0 \times q) + (1 \times p)] - p^2\)

d’où \(V(X) = p - p^2 = p (1 - p) = pq\)

2.3.1 Définition

Décrite pour la première fois par Isaac Newton en 1676 et démontrée pour la première fois par le mathématicien suisse Jacob Bernoulli en 1713, la loi binomiale est l’une des distributions de probabilité les plus fréquemment rencontrées en statistique appliquée.

Soit l’application \(S_n : \Omega^n \longrightarrow \mathbb{R}^n\)

avec \(S_n = X_1 + X_2 +...+ X_i + ...+ X_n\) où \(X_i\) est une variable de Bernoulli

La variable binomiale, \(S_n\), représente le nombre de succès obtenus lors de la répétition de \(n\) épreuves identiques et indépendantes, chaque épreuve ne pouvant donner que deux résultats possibles.

La probabilité que \(S_n= k\), c’est à dire l’obtention de \(k\) succès au cours de \(n\) épreuves indépendantes est :

Il est facile de démontrer que l’on a bien une loi de probabilité car :

\(\sum\limits_{k * 0}^n {P({S_n}} = k) = \sum\limits_{k = 0}^n {C_n^k} {p^k}{q^{n - k}} = {(p + q)^n} = 1\) car \(p + q = 1\)

Remarque : Le développement du binôme de Newton \((p+q)^n\) permet d’obtenir l’ensemble des probabilités pour une distribution binomiale avec une valeur \(n\) et \(p\) donnée. Il existe également des tables de la loi binomiale où les probabilités sont tabulées pour des valeurs \(n\) et \(p\) données.

Exemple:

Dans une expérience sur le comportement du rat, rattus norvegicus, on fait pénétrer successivement \(n\) rats dans un labyrinthe en forme de H. On étudie alors la probabilité que \(k\) rats empruntent la branche supérieure droite du H.

A chaque épreuve, deux évènements peuvent se produire : soit le rat suit l’itinéraire voulu (succès) soit il ne l’emprunte pas (échec). Sachant qu’il y a 4 itinéraires possibles (branches), la probabilité du succès \(p = 1/4\).

Hypothèse :

• si les rats n’ont pas été conditionnés,

• si la branche supérieure droite ne comporte aucun élément attractif ou répulsif,

• si le choix de l’itinéraire d’un rat n’affecte pas le choix du suivant (odeurs)

alors : la variable aléatoire \(X\) « itinéraire emprunté pour \(x\) rats » suit une loi binomiale

dont la distribution des probabilités est la suivante si l’on étudie le comportement de 5 rats :

Remarque :

Il est possible d’obtenir aisément les valeurs des combinaisons de la loi binomiale en utilisant le triangle de Pascal. De plus on vérifie que la somme des probabilités est bien égale à 1.

2.3.2 Espérance et variance

L’espérance d’une variable binomiale \(S_n\) est égale à \(E(S_n) = n p\)

en effet \(E ( S_n ) = E ( X_1 + X_2 +...+ X_i + ...+ X_n )\)

or \(E ( X_1 + X_2 +...+ X_i + ...+ X_n ) = \sum\limits_{i = 1}^n {E(X_i)}\) propriété de l’espérance

et \(E(S_n) = \sum\limits_{i = 1}^n {E(X_i)} = \sum\limits_{i = 1}^n p\) avec \(E ( X_i ) = p\) variable de Bernoulli

d’où \(E(S_n) = n p\)

La variance d’une variable binomiale \(S_n\) est égale à \(V ( S_n ) = n p q\)

en effet \(V ( S_n ) = V ( X_1 + X_2 +...+ X_i + ...+ X_n )\)

or \(V ( X_1 + X_2 +...+ X_i + ...+ X_n ) = \sum\limits_{i = 1}^n V ( X_i )\) propriété de la variance

et \(V(S_n) = \sum\limits_{i = 1}^n {V({X_i}) = \sum\limits_{i = 1}^n {pq} } \qquad\) avec \(V ( X_i )\) = pq car variable de Bernoulli

d’où \(V ( S_n ) = n p q\)

Exemple :

Dans le cadre de l’étude de comportement du rat , quel est en moyenne le nombre attendu de rats qui vont emprunter l’itinéraire prévu si l’expérience porte sur un lot de 20 rats ? Donnez également la variance et l’écart type de cette variable ? Réponse.

2.3.3 Symétrie et récurrence de la loi binomiale

La loi binomiale dépend des deux paramètres \(n\) et \(p\). Elle est symétrique pour \(p = 0,5\) et dissymétrique pour les autres valeurs de \(p\). La dissymétrie est d’autant plus forte :

1. pour \(n\) fixe, que \(p\) est différent de \(q\) (graphe)

2. pour \(p\) fixe que \(n\) est plus petit.

Afin de faciliter les calculs des probabilités, il est possible d’utiliser une formule de récurrence donnant les valeurs des probabilités successives :

2.3.4 Stabilité de la loi binomiale

2.4.1 Approximation d’une loi binomiale

Lorsque \(n\) devient grand, le calcul des probabilités d’une loi binomiale

\(P({S_n} = k) = C_n^k{p^k}{q^{n - k}}\)

devient très fastidieux. On va donc, sous certaines conditions, trouver une approximation de \(p_k\) plus maniable.

Remarque :

Cette approximation est correcte si \(n ≥ 50\) et \(n p ≤ 5\).

Exemple :

Soit une loi binomiale de paramètres \((100 ; 0,01)\), les valeurs des probabilités pour \(k\) de \(0\) à \(5\) ainsi que leur approximation à \(10^-3\) avec une loi de Poisson de paramètre \((\lambda = n p = 1)\) sont données dans le tableau ci-dessous :

Dans le cas de cet exemple où \(n =100\) et \(np =1\), l’approximation de la loi binomiale par une loi de poisson donne des valeurs de probabilités identiques à \(10^-3\) près.

2.4.2 Loi de Poisson

On appelle processus poissonnien (ou processus de Poisson), le modèle probabiliste des situations qui voient un flux d’évènements se produire les uns à la suite des autres de façon aléatoire (dans le temps et dans l’espace), obéissant aux conditions suivantes :

• la probabilité de réalisation de l’évènement au cours d’une petite période ou sur une petite portion d’espace \(\Delta t\) est proportionnelle à \(\Delta t\) soit \(p \Delta t\) .

• elle est indépendante de ce qui s’est produit antérieurement ou à côté,

• la probabilité de deux apparitions sur le même D\(t\) est négligeable.

Ainsi, des évènements qui se réalisent de façon aléatoire comme des pannes de machines, des accidents d’avions, des fautes dans un texte, …peuvent être considérés comme relevant d’un processus poissonnien.

Remarque : Une loi de Poisson est donnée par sa loi de probabilité :

1. \(\forall k , P ( X = k ) > 0\)

2. \(\sum\limits_{k \geq 0} {P(X=k)} = \sum\limits_{k \geq 0} { \frac{ e^{- \lambda} \lambda^k} { k! } } = e^{- \lambda} \sum\limits_{k \geq 0} { \frac{ \lambda^k} { k! } }\) or \(\sum\limits_{k \geq 0} {\frac{{{\lambda ^k}}}{{k!}}} = {e^\lambda }\)

d’où \(\sum\limits_{k \geq 0} {P(X = k)} = {e^{ - \lambda }}{e^\lambda } = 1\)

Exemple :

Une suspension bactérienne contient 5000 bactéries/litre. On ensemence à partir de cette suspension, 50 boites de Pétri, à raison d’1 cm³ par boite. Si \(X\) représente le nombre de colonies par boite, alors la loi de probabilité de \(X\) est :

\(X \rightarrow \mathcal{P} ( \lambda = 5)\)

La probabilité qu’il n’y ait aucune colonie sur la boite de Pétri est : \(P(X = 0) = \frac{5^0 e^{ - 5} } {0!} =\) 0,0067 soit approximativement 0,67 % de chance.

La probabilité qu’il n’y ait au moins une colonie sur la boite de Pétri est :

\(P(X > 0)=1- P(X = 0) = 1-0,0067 =\) 0,9933 soit 99,3 % de chance d’avoir au moins une colonie bactérienne qui se développe dans la boite de Pétri. (?theme=proba&chap=2#Evènement contraire))

2.4.3 Espérance et variance

L’espérance d’une variable aléatoire de Poisson est \(E(X) = \lambda\)

Par définition \(E(X) = \sum\limits_{k \geq 0} {k{p_k}} = \sum\limits_{k \geq 0} { k \frac{ { \lambda^k e^{ - \lambda }}}{k!}}\) avec \(k \in \mathbb{N}\) valeurs prises par la v.a. \(X\)

avec \(\sum\limits_{k \geq 0} {\frac{{{\lambda ^k}}}{{k!}} = [ {\lambda + \frac{{{\lambda ^2}}}{{1!}} + \frac{{{\lambda ^3}}}{{2!}} + .... + \frac{{{\lambda ^{k + 1}}}}{{k!}}} ]} = \lambda [ {1 + \frac{\lambda }{{1!}} + \frac{{{\lambda ^2}}}{{2!}} + ... + \frac{{{\lambda ^k}}}{{k!}}} ]\)

d’où \(E(X) = \lambda {e^{ - \lambda }}\sum\limits_{k > 0} {\frac{{{\lambda ^k}}}{{k!}}} = \lambda {e^{ - \lambda }}{e^\lambda } = \lambda\)

La variance d’une variable de Poisson est \(V(X) = \lambda\)

Par définition \(V(X) = \sum\limits_{k \geq 0} {{k^2}{p_k} - E{{(X)}^2}} = \sum\limits_{k \geq 0} {{k^2}\frac{{{\lambda ^k}{e^{ - \lambda }}}}{{k!}} - {\lambda ^2}}\)

en posant \({k^2} = k + k(k - 1)\), alors

\(\sum\limits_{k \geq 0} {{k^2}\frac{{{\lambda ^k}{e^{ - \lambda }}}}{{k!}} = \sum\limits_{k \geq 0} {\frac{k}{{k!}}} } {\lambda ^k}{e^{ - \lambda }} + \sum\limits_{k \geq 0} {\frac{{k(k - 1)}}{{k!}}} {\lambda ^k}{e^{ - \lambda }}\)

d’où \(\sum\limits_{k \geq 0} {k^2}\frac{{{\lambda ^k}{e^{ - \lambda }}}}{{k!}} = {e^{ - \lambda }}[ {\lambda + \frac{{{\lambda ^2}}}{{1!}} + \frac{{{\lambda ^3}}}{{2!}} + ... + \frac{{{\lambda ^{k + 1}}}}{{k!}}} ] + {e^{ - \lambda }}[ {{\lambda ^2} + \frac{{{\lambda ^3}}}{{1!}} + \frac{{{\lambda ^4}}}{{2!}} + .... + \frac{{{\lambda ^{k + 2}}}}{{k!}}} ]\)

d’où \(\sum\limits_{k \geq 0} {k^2}\frac{{{\lambda ^k}{e^{ - \lambda }}}}{{k!}} ={\lambda ^2}{e^{ - \lambda }}\sum\limits_{k \geq 0} {\frac{{{\lambda ^k}}}{{k!}}} + \lambda {e^{ - \lambda }}\sum\limits_{k \geq 0} {\frac{{{\lambda ^k}}}{{k!}}}\)

d’où \(V(X) = {\lambda ^2}{e^{ - \lambda }}{e^\lambda } + \lambda {e^{ - \lambda }}{e^\lambda } - {\lambda ^2} = \lambda\)

Remarque :

Il est à noter que dans le cas d’une variable aléatoire de Poisson, l’espérance et la variance prennent la même valeur. Ceci est un élément à prendre en compte lors des tests de conformité à une loi de probabilité.

Exemples :

Dans le cadre de la culture bactérienne, le nombre moyen de colonies attendu sur la boite de Pétri est : \(E(X) = \lambda =\) 5 colonies.

Ainsi si l’on effectue plusieurs cultures bactériennes (plusieurs boites de Pétri) à partir de la même solution initiale, on attend en moyenne cinq colonies pour l’ensemble des boites.

En ce qui concerne la variance et l’écart-type , on aura :

\(V(X) = \lambda = 5\) et \(\sigma (X) = \sqrt {V(X)} =\) 2,24 colonies.

2.4.4 Stabilité de la loi de Poisson

2.5.1 Définition

Sous le schéma de Bernoulli (épreuves identiques et indépendantes), on désire obtenir \(n\) succès et l’on considère la variable aléatoire discrète \(X\) qui représente le nombre d’épreuves indépendantes \(k\) nécessaire à l’obtention des \(n\) succès.

Remarque :

Dans le cas de la loi binomiale négative, le nombre de succès \(n\) est connu et l’on cherche le nombre d’épreuves \(k\), nécessaire pour obtenir les \(n\) succès. Ainsi le dernier évènement est connu car les épreuves cessent avec l’obtention du \(n\)^ieme succès et l’on choisit \(n-1\) objets parmi \(k-1\).

Exemple :

Pour étudier le domaine vital d’une population de poissons, des émetteurs radio sont fixés au niveau de la nageoire dorsale après une légère anesthésie locale. Suite à divers aléas, on considère que 30 % des poissons équipés ne sont pas repérés par la suite. Si l’on considère qu’un minimum de 15 poissons doivent être suivis pour avoir des résultats statistiquement acceptables, la variable aléatoire \(X\) « nombre de poissons devant être équipés » suit une loi binomiale négative

\(X \rightarrow \mathrm{B}N (15, 0,70)\)

En posant comme hypothèse que les causes de pertes de liaisons radio soient suffisamment nombreuses pour assurer l’indépendance entre chaque épreuve, la probabilité d’être obligé d’équiper 20 poissons est de :

\(P(X = 20) = \frac{{19!}}{{14!\;5!}}{(0,70)^{15}}{(0,30)^5} =\) 0,13

2.5.2 Espérance et variance

L’espérance associée à une loi binomiale négative est : \(E(X) = \frac{n}{p}\)

La variance associée à une loi binomiale négative est : \(V(X) = n \frac{q}{p^2}\)

2.5.3 Loi géométrique

Voici pourquoi :

Si l’on considère la variable aléatoire \(X\) « nombre de naissances observées avant l’obtention d’une fille » avec \(p = 1/2\) (même probabilité de naissance d’une fille ou d’un garçon), la loi suivit par \(X\) est une loi géométrique car :

\(X = 1\) si \(\{X = F\}\) avec \(P(X = 1) = p\)

\(X = 2\) si \(\{X = G ∩ F\}\) avec \(P(X = 2) = q p\)

\(X = 3\) si \(\{X= G ∩ G ∩ F\}\) avec \(P(X = 3) = q q p = q 2 p\)

d’où \(X = k\) si \(\{ X = G ∩ G ∩...∩.G ∩ F\}\) avec \(k-1\) \(\{X=G\}\) et donc \(P( X = k) = pq^{k-1}\)

D’où l’espérance associée à la loi géométrique est : \(E(X) = \frac{1}{p}\)

et la variance associée à la loi géométrique est : \(V(X) = \frac{q}{p^2}\)

3.1.1 Définition

La loi uniforme est la loi exacte de phénomènes continus uniformément répartis sur un intervalle.

Quelques commentaires :

1. La loi uniforme continue étant une loi de probabilité, l’aire hachurée en rouge sur la figure ci-dessus vaut 1. Ceci implique que la valeur prise par \(f(x)\) vaut \(\frac{1}{b - a}\).

2. La probabilité que \(X \in [a’,b’]\) avec \(a’ < b\)’ et \(a’, b’ \in [a,b]\) vaut :

\(P(a' \leq X \leq b') = \int_{a'}^{b'} {f(x)dx = \int_{a'}^{b'} {\frac{{dx}}{{b - a}}} } = \frac{{b' - a'}}{{b - a}}\)

3. La fonction de répartition associée à la loi uniforme continue est telle que :

\(F_X (x) = 0\) si \(x < a\)

\(F_X (x) = 1\) si \(x > b\)

\(F_X (x) = \frac{x-a}{b-a}\) si \(a \leq x \leq b\)

3.1.2 Espérance et variance

L’espérance de la loi uniforme continue vaut : \(E(X) = \frac{b + a}{2}\)

En effet par définition \(E(X) = \int_{ - \infty }^{ + \infty } {x f(x) dx}\)

\(E(X) = \int_{ - \infty }^a {x f(x) dx} + \int_a^b {x f(x) dx } + \int_b^{ + \infty } {x f(x) dx}\) cours analyse (Intégrale)

or \(\int_{ - \infty }^a x f(x)dx = 0\) et \(\int_b^{ + \infty } xf(x)dx = 0\) par définition de la loi uniforme continue

d’où \(E(X) = \int_a^b x\frac{1}{b - a} dx = \frac{1}{b - a} \int_a^b {x d x} = \frac{1}{b - a} [ {\frac{x^2}{2}} ]_ {a} ^b\)

\(E(X) = \frac{1}{{2(b - a)}} [ {{b^2} - {a^2}} ] = \frac{1}{{2(b - a)}} ( {b - a} ) ( {b + a} ) = \frac{{b + a}}{2}\)

La variance de la loi uniforme continue vaut : \(V(X) = \frac{ (b - a)^2 }{12}\)

En effet par définition \(V(X) = \int_{ - \infty }^{ + \infty } { {x^2} f(x) dx - E(X)^2 }\)

\(V(X) = \int_a^b {x^2 \frac{dx}{b - a} - E(X)^2}\) même simplification que pour l’espérance

\(V(X) = \frac{1}{b - a} [ \frac{x^3}{3} ]_ a ^ b - E(X)^2 = \frac{1}{b - a} [ \frac{b^3 - a^3}{3} ] - { [ {\frac{b + a}{2}} ]^2}\)

or \(\frac{1}{{b - a}}[ {\frac{{{b^3} - {a^3}}}{3}} ] = \frac{1}{3}({b^2} + ab + {a^2})\) et \([ {\frac{{{{(b + a)}^2}}}{4}} ] = \frac{1}{4}({b^2} + 2ab + {a^2})\)

d’où \(V(X) = \frac{1}{b - a} [ \frac{ b^3 - a^3}{3} ] - [ \frac{(b + a)^2}{4} ] = \frac{(b - a)^2}{12}\)

3.2.1 Définition

On parle de loi normale lorsque l’on a affaire à une variable aléatoire continue dépendant d’un grand nombre de causes indépendantes dont les effets s’additionnent et dont aucune n’est prépondérante (conditions de Borel). Cette loi acquiert sa forme définitive avec Gauss (en 1809) et Laplace (en 1812). C’est pourquoi elle porte également les noms de : loi de Laplace, loi de Gauss et loi de Laplace-Gauss.

Exemple :

Ainsi la taille corporelle d’un animal dépend des facteurs environnementaux (disponibilité pour la nourriture, climat, prédation, etc.) et génétiques. Dans la mesure où ces facteurs sont indépendants et qu’aucun n’est prépondérant, on peut supposer que la taille corporelle suit une loi normale.

Remarque :

On admet que \(\int_{ - \infty }^{ + \infty } {f(x)dx} =1\) dans la mesure où l’intégration analytique est impossible.

3.2.2 Etude de la fonction densité de probabilité

La fonction \(f\) est paire autour d’un axe de symétrie \(x = \mu\) car \(f(x + \mu ) = f(\mu - x)\)

d’où \(D_E = [\mu , +\infty[\)

La dérivé première \(f’(x)\) est égale à : \(f’(x) = - ( {\frac{x - \mu }{\sigma ^2}} )f(x)\) Démonstration

d’où \(f’(x) = 0\) pour \(x = \mu\) et \(f’(x) < 0\) pour \(x > \mu\)

La dérivé seconde \(f’’(x)\) est égale à : \(f’’(x) = - \frac{1}{\sigma ^2}( {1 - \frac{(x - \mu )^2}{\sigma ^2} } )f(x)\) Démonstration

d’où \(f’’(x) = 0\) pour \(x = \mu + \sigma\) et \(f’’(x) > 0\) pour \(x > \mu + \sigma\)

Remarque :

Le paramètre \(\mu\) représente l’axe de symétrie et \(\sigma\) le degré d’aplatissement de la courbe de la loi normale dont la forme est celle d’une courbe en cloche.

3.2.3 Espérance et variance

L’espérance de la loi normale vaut : \(E(X) = \mu\)

La variance de la loi normale vaut : \(V(X) = \sigma^2\)

3.2.4 Stabilité de la loi normale

Voici pourquoi :

1. \(E(X_1 +X_2 ) = E(X_1 ) + E(X_2 )\) Propriété \(P_1\) de l’espérance.

or \(E(X_1 ) = \mu_1\) et \(E(X_2 ) = \mu_2\) d’où \(E(X_1 +X_2 ) = \mu1 + \mu2\)

2. \(V(X_1 +X_2 ) = V(X_1 ) + V(X_2 )\) Propriété \(P_1\) de la variance lorsque \(X_1\) et \(X_2\) sont indépendantes.

or \(V(X_1) = {\sigma_1}^2\) et \(V(X_2) = {\sigma_2}^2\) d’où \(V(X_1 +X_2 ) = {\sigma_1}^2 + {\sigma_2}^2\)

Ce théorème se généralise immédiatement à la somme de \(n\) variables aléatoires normales indépendantes.

3.3.1 Définition

Remarque : \(f\) est bien une loi de probabilité car :

• \(\forall x \in \mathbb{R}, \qquad f(x) ≥ 0\)

• \(f\) est intégrable sur \(]-\infty, + \infty[\) et \(\int_{ - \infty }^{ + \infty } {f(x)dx = 1}\)

3.3.2 Etude de la fonction densité de probabilité

La fonction \(f\) est paire car \(f(-x) = f(x)\) d’où \(D_E = [0,+\infty [\)

La dérivé première est \(f’(x) = -x f(x)\) avec \(f ’(x) ≤ 0\) pour \(x ≥ 0\).

La dérivée seconde est \(f ’’(x) = -f(x) + x f(x) = (x –1) f(x)\) qui s’annule pour \(x = 1\) sur \(D_E\) .

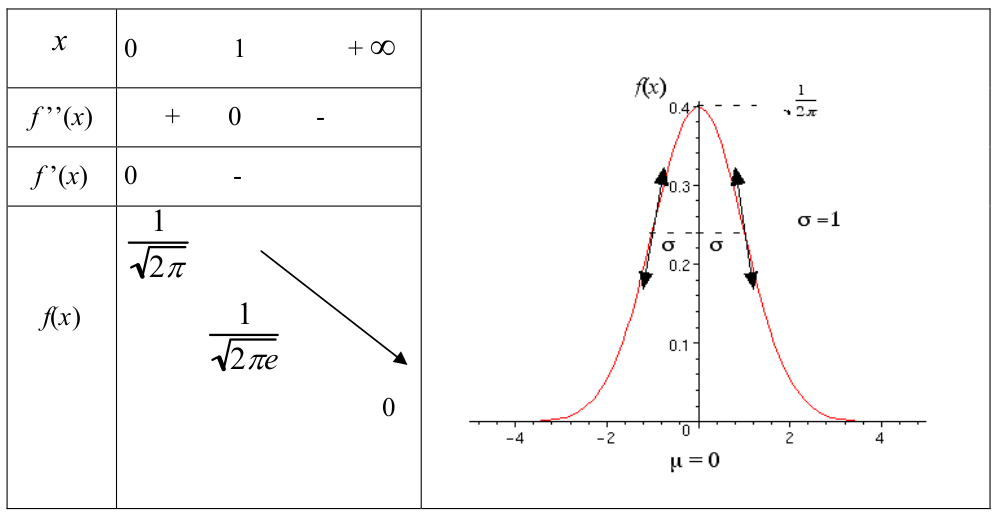
Remarque : L’axe de symétrie correspond à l’axe des ordonnées \((x = 0)\) et le degré d’aplatissement de la courbe de la loi normale réduite est 1.

3.3.3 Espérance et variance

L’espérance d’une loi normale réduite est : \(E(X) = 0\)

En effet par définition \(E(X) = \int_{ - \infty }^{ + \infty } {x f(x) dx}\).

Or la fonction à intégrer est impaire d’où \(E(X)=0\) (cours d’analyse : intégrale)

La variance d’une loi normale réduite est : \(V(X) = 1\)

En effet par définition \(V(X) = \int_{ - \infty }^{ + \infty } {x^2}f(x)dx - E{(X)^2}\)

d’où \(V(X) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^{ + \infty } {{x^2}{e^{ - \frac{{{x^2}}}{2}}}dx }\)

En effectuant une intégration par partie :

\(V(X) = \frac{1}{{\sqrt {2\pi } }}( {[ { - x{e^{ - \frac{{{x^2}}}{2}}}} ]_ { - \infty }^{ + \infty } - \int_{ - \infty }^{ + \infty } { - {e^{ - \frac{{{x^2}}}{2}}}dx } } )\) avec \(( {[ { - x{e^{ - \frac{{{x^2}}}{2}}}} ]_ { - \infty }^{ + \infty }} ) = 0\)

or \(V(X) = \frac{1}{{\sqrt {2\pi } }}\int_ { - \infty }^{ + \infty } {{e^{ - \frac{{{x^2}}}{2}}}dx } =1\) par définition d’une fonction de répartition

d’où \(V(X) = 1\)

3.3.4 Relation avec la loi normale

3.3.5 Calcul des probabilités d’une loi normale

La fonction de répartition de la loi normale réduite permet d’obtenir les probabilités associées à toutes variables aléatoires normales N (m,s) après transformation en variable centrée réduite.

Une application directe de la fonction \(\pi\) est la lecture des probabilités sur la table de la loi normale réduite.

3.4.1 Loi du \({\chi ^2}\) de Pearson

Définition:

La loi de Pearson ou loi de \({\chi ^2}\) (Khi deux) trouve de nombreuses applications dans le cadre de la comparaison de proportions, des tests de conformité d’une distribution observée à une distribution théorique et le test d’indépendance de deux caractères qualitatifs. Ce sont les test du khi-deux.

Remarque :

Si \(n =1\), la variable du \({\chi ^2}\) correspond au carré d’une variable normale réduite de loi \(\mathcal{N}(0 , 1)\) (?theme=proba&chap=3).

Propriétés :

Remarque :

La constante \(C(n)\) est telle que \(\int_{ - \infty }^{ + \infty } {f(x)dx = 1}\). La distribution du \({\chi ^2}\) est dissymétrique et tend à devenir symétrique lorsque \(n\) augmente en se rapprochant de la [distribution normale](?theme=proba&chap=3 à laquelle elle peut être assimilée lorsque \(n > 30\).

Espérance et variance

L’espérance de la variable du \({\chi ^2}\) est : \(E(\chi ^2) = n\)

car par définition \(E(\chi ^2) = \sum\limits_{i = 1}^n {E(X_i^2} )\) avec \(X_i\) variable normale réduite

or \(V(X_i ) = E({X_i}^2 ) - {E(X_i )}^2 = 1\) pour la variable normale réduite avec \(E(X_i ) = 0\)

d’où \(E({X_i}^2 ) = 1\) et donc \(E(\chi ^2) = n\)

La variance de la variable du \({\chi ^2}\) est : \(V({\chi ^2}) = 2n\)

car par définition les \(X_i\) variables normales réduites étant indépendantes,

\(V({\chi ^2}) = \sum\limits_{i = 1}^n V({X_i}^2)\) et d’autre part \(V({X_i}^2) = E({X_i}^4 ) – [ E({X_i}^2 )]^2\)

or \(E({X_i}^4 ) = 3\) d’où \(V({X_i}^2) = 3 – 1 = 2\)

ainsi \(V({\chi ^2}) = \sum\limits_{i = 1}^n {V(X_i^2} )= 2n\)

4.3.1 La loi binomiale

Remarque :

On considère que l’approximation est valable si on a à la fois \(np > 5\) et \(nq > 5\) (?theme=proba&chap=4).

4.3.2 Loi de Poisson

Remarque :

On considère qu’on peut faire ces approximations si \(\lambda \geq 20\) (?theme=proba&chap=4).

4.4.1 Inégalité de Markov

Soit \(X\) une variable aléatoire admettant une espérance \(E(X)\) et une variance \(V(X)\), étant donné, un réel \(h>0\) l’inégalité de Markov donne :

Voici pourquoi :

\(P(| X | \geq h) = \sum\limits_{i \in I} {p_i}\) la sommation étant étendue à toutes les valeurs de \(i\) tels que \(|x_i| > h\)

dans ce cas : \(| {\frac{{{x_i}}}{h}} | \geq 1\) soit \(1 \leq \frac{{x_i^2}}{{{h^2}}} \Leftrightarrow {p_i} \leq {p_i}\frac{{x_i^2}}{{{h^2}}}\)

ainsi \(\sum\limits_{i \in I} {{p_i}} \leq \frac{1}{{{h^2}}}\sum\limits_{i \in I} {{p_i}x_i^2}\) d’où \(\sum\limits_{i \in I} {{p_i}} \leq \frac{1}{{{h^2}}}E({X^2})\) et \(P(| X | \geq h) \leq \frac{1}{{{h^2}}}E({X^2})\)

4.4.2 Inégalité de Bienaymé-Tchébycheff

Si l’on applique l’inégalité de Markov à la variable aléatoire \(X - \bar {X}\), on a

\(P( |X - \bar{X}| \geq h ) \leq \frac{1}{h^2} E[ (X - \bar{X} )^2 ]\)

or \(E[{(X - \bar{X} )^2}] = V(X) = {\sigma ^2}\) et en passant à l’évènement contraire, on a :

\(P(| {X - \bar{X} } | \leq h) \geq 1 - \frac{{{\sigma ^2}}}{{{h^2}}}\)

En posant \(h = t\sigma0\) avec \(t > 0\), on obtient l’inégalité suivante

\(P(| {\frac{{X - \bar{X} }}{\sigma }} | \leq t) \geq 1 - \frac{1}{{{t^2}}}\) sachant que \(\sigma > 0\)

qui est équivalente à

Remarque : Ces inégalités n’ont d’intérêt que si \(t\) est assez grand.