Chapitre 4 — Fonctions usuelles
Introduction
L’objectif de ce chapitre est de donner des exemples d’utilisation en Biologie des fonctions réelles d’une variable réelle les plus usitées : les fonctions linéaires, les fonctions homographiques, les fonctions trigonométriques, les fonctions hyperboliques, les fonctions logarithme et exponentielle, et les fonctions puissance.
Chaque paragraphe sera consacré à un type de fonction et sera organisé en deux parties : la première présentera de brefs mais indispensables rappels sur la fonction, en s’appuyant sur les notions développées dans les précédents chapitres (1, 2 et 3) ainsi que sur des représentations graphiques ; la seconde partie s’attachera, dans la mesure du possible, à donner une illustration en Biologie du type de fonction étudié.
1 Fonctions polynômes élémentaires
1.1 Fonctions polynômes de degré 1
1.1.1 Définition et propriétés
Définition :
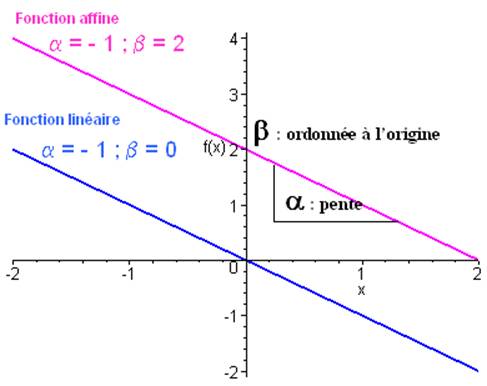
Une fonction polynôme de degré 1 \(f\) est une fonction dépendant de deux paramètres réels $$ et $$ et définie pour tout \(x \in \mathbb{R}\) par :
$f( x ) = x + $ avec \(\alpha \ne 0\)
La fonction polynôme de degré 1 \(f\) a une dérivée première constante égale à $$ ; elle est strictement croissante si \(\alpha > 0\) et strictement décroissante si \(\alpha < 0\).
Il découle de la définition que :
\(\forall {x_1},{x_2} \in \mathbb{R}\), on a \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \alpha \left( {{x_1} - {x_2}} \right)\)
ê L’ accroissement d’une fonction polynôme de degré 1 (\(f\left( {{x_1}} \right) - f\left( {{x_2}} \right)\)) sont proportionnels à ceux de la variable \(\left( {{x_1} - {x_2}} \right)\).
ê \(\alpha * \frac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}}\) est appelé pente de la fonction polynôme de degré 1
\(\beta = f\left( 0 \right)\) ; si \(\beta * 0\), on dit que la fonction est linéaire.
Le graphe d’une fonction polynôme de degré 1 est une droite de pente $$ passant par le point de coordonnées \(\left( {0,\beta } \right)\) ; $$ est l’ordonnée à l’origine.
Unnamed Image
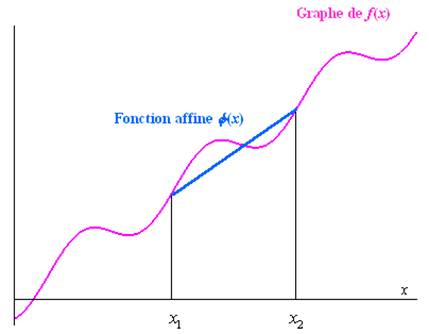
1.1.2 Application : interpolation linéaire
L’interpolation linéaire d’une fonction \(f\) dans un intervalle \(\left[ {{x_1};{x_2}} \right]\) est la fonction polynôme de degré 1 $$ prenant les mêmes valeurs que \(f\) aux bornes de l’intervalle \(\left[ {{x_1};{x_2}} \right]\) :
\(\varphi \left( {{x_1}} \right) = f\left( {{x_1}} \right)\) \(\varphi \left( {{x_2}} \right) = f\left( {{x_2}} \right)\)
Unnamed Image
1.1.3 Un exemple en Biologie
Revoir l’exemple en Biologie présenté au Chapitre 1, §7.
1.2 Polynômes du second degré
1.2.1 Définition et propriétés
Définition :
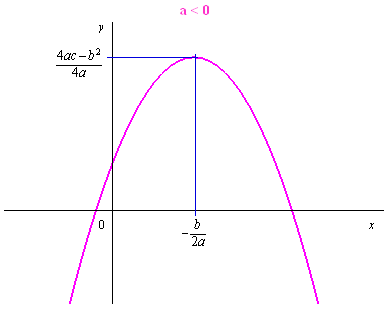
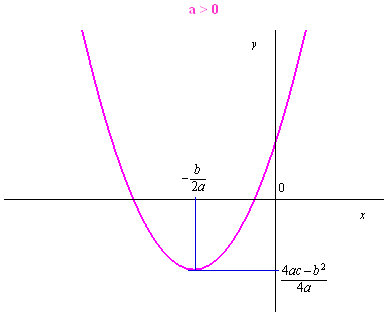
Un polynôme du second degré est une fonction \(f\) dépendant de trois paramètres réels \(a,b,c\) et définie par : * \(f\left( x \right) = a{x^2} + bx + c\) avec \(a \ne 0\)
La fonction \(f\) est continue et dérivable en tout point : \(f'\left( x \right) = 2ax + b\).
La dérivée seconde est constante et égale à 2\(a\).
\(f\) admet un extremum en \(x = * \frac{b}{{2a}}\) : \(f\left( { - \frac{b}{{2a}}} \right) * \frac{{4ac - {b^2}}}{{4a}}\).
Lorsque \(x\) tend $ $, \(f\) admet pour limite $ $ selon le signe de \(a\).
La représentation graphique d’un polynôme du second degré est une parabole :
 *
*
Unnamed Image
Nous ne reviendrons pas ici sur la recherche des racines d’un polynôme du second degré.
Rappelons simplement que :
Si \(\Delta = {b^2} - 4ac < 0\), alors \(a{x^2} * bx + c = 0\) n’admet aucune racine réelle ;
Si \(\Delta = {b^2} - 4ac = 0\), alors \(a{x^2} * bx + c = 0\) admet une racine double : \({x_0} * - \frac{b}{{2a}}\) ;
Si \(\Delta = {b^2} - 4ac > 0\), alors \(a{x^2} * bx + c = 0\) admet deux racines :
\({x_1} = \frac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}}\) \({x_2} * \frac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}\)
Dans ce cas \({x_1} * {x_2} = \frac{{ - b}}{a}\) et \({x_1}{x_2} = \frac{c}{a}\).
1.2.2 Un exemple en Biologie
Pour de nombreuses espèces (mammifères, poissons, micro-organismes), il est raisonnable de considérer qu’en première approximation, la relation du taux de croissance de la population avec la température de l’environnement est un polynôme du second degré :
\(\mu = a{T^2} + bT + c\)
Les valeurs de \(a\), \(b\) et \(c\) vont dépendre de l’espèce considérée.
Remarquons que d’un point de vue biologie, il faut nécessairement que \(\mu \geqslant 0\), ce qui n’est pas nécessairement le cas pour \(T\).
On sait qu’il existe pour chaque individu un optimum de croissance (\({T_{opt}}\)), ainsi que des températures minimale (\({T_{\min }}\)) et maximale (\({T_{\max }}\)) de croissance en deça et au-delà desquelles il n’y a plus de croissance. Ainsi, les paramètres \(a\), \(b\) et \(c\) doivent vérifier les équations suivantes :
\(\mu '\left( {{T_{opt}}} \right) = 0\)
\(\mu \left( {{T_{\min }}} \right) = \mu \left( {{T_{\max }}} \right) = 0\)
\({T_{opt}} = - \frac{b}{{2a}}\) \({T_{\min }} = \frac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}}\) \({T_{\max }} = \frac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}}\)
Chez la bactérie Methylosinus trichosporium,* *qui est à la fois méthanotrophe et mésophile, on connaît approximativement \({T_{opt}} * 23^\circ C\) qui correspond à \({\mu _{\max }} = 0.012\;{{\text{h}}^{ - 1}}\) et \({T_{\min }} = 9^\circ C\) (Kevbrina et al., 2001).
D’après le modèle polynomial, on en déduit que \({T_{\max }}\) doit être égal à 37°C, ce que l’on vérifie presque expérimentalement puisqu’en fait \({T_{\max }} = 37^\circ C\).
On obtient le graphe suivant, où la relation \(\mu * f\left( T \right)\) n’est représentée que pour des valeurs positives de µ, c’est-à-dire pour \(T \in \left[ {9^\circ C{\text{ ; }}37^\circ C} \right]\) :
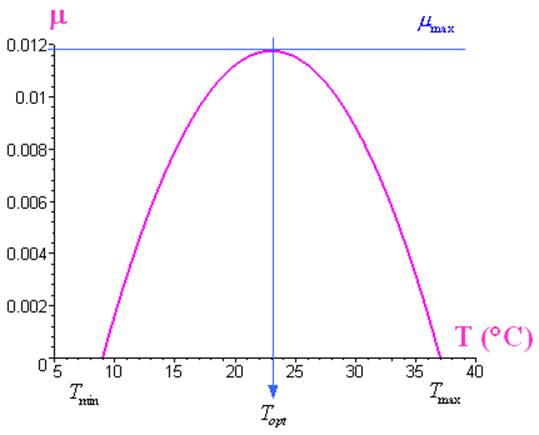
Unnamed Image
Relation \(\mu * f\left( T \right)\) pour la bactérie Methylosinus trichosporium
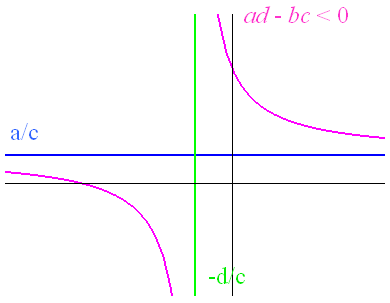
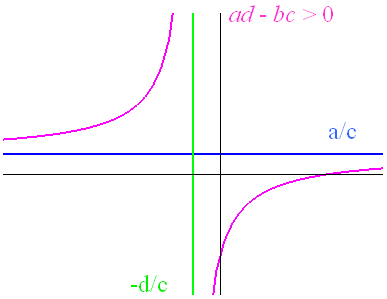
Les limites à droite et à gauche de $ - $ dépendent du signe de \(ad - bc\) :
Si \(ad * bc > 0\), alors ${x } h( x ) = - $ et ${x } h( x ) = + $
Si \(ad * bc < 0\), alors ${x } h( x ) = + $ et ${x } h( x ) = - $
La fonction \(h\) est continue et dérivable sur \({D_h}\) :
\(h'\left( x \right) = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\) : le sens de variation de \(h\) dépend du signe de \(ad - bc\)
Si \(ad * bc > 0\), alors la fonction \(h\) est croissante ;
Si \(ad * bc < 0\), alors la fonction \(h\) est décroissante ;
Si \(ad * bc = 0\), la fonction \(h\) est constante et égale à \(\frac{a}{c} * \frac{b}{d}\)
Si \(ad * bc \ne 0\), deux cas de figure peuvent se présenter (voir Figures)
Le graphe d’une fonction homographique est une hyperbole équilatère, qui admet pour asymptote les deux droites d’équation \(x = * \frac{d}{c}\) et \(y = \frac{a}{c}\) ; le point d’intersection des deux asymptotes est un centre de symétrie pour le graphe.
 *
*
Unnamed Image
1.3.2 Un exemple en Biologie : d’après Legay et al. (1981), p60
Une réaction enzymatique peut se symboliser par le schéma suivant :
\(S\xrightarrow{E}P\)
qui se lit : « le substrat \(S\) est transformé par l’enzyme \(E\) en un produit \(P\) ».
Quantitativement, on décrit l’évolution d’une telle réaction par sa cinétique exprimée en terme de vitesse de réaction V :
\(V = - \frac{{d\left[ S \right]}}{{dt}} = \frac{{d\left[ P \right]}}{{dt}}\) avec \(t\) le temps de réaction
où \(\left[ S \right]\) est la concentration en substrat \(S\) et \(\left[ P \right]\) la concentration en produit \(P\).
\(V = \frac{{{V_{\max }}\left[ S \right]}}{{{K_M} + \left[ S \right]}} = V\left( {\left[ S \right]} \right)\) avec \({V_{\max }}\) et \({K_M}\) des constantes strictement positives
On suppose vérifiées les conditions suivantes :
- \(t = 0\), on a \(\left[ S \right] = {S_0}\) et \(\left[ P \right] = 0\)
\(\forall t \geqslant 0\), on a \(\left[ S \right] + \left[ P \right] * {S_0}\) : \(\left[ P \right] = {S_0} - \left[ S \right]\)
Mathématiquement, le domaine de définition de \(V\) est \({D_V} * \left] { - \infty ; - {K_M}} \right[ \cup \left] { - {K_M}; + \infty } \right[\), mais biologiquement, il faut que \(V \geqslant 0\). Comme \(\left[ S \right] \geqslant 0\) (c’est une concentration), on étudie \(V\) sur l’intervalle \(\left[ {0; + \infty } \right[\).
\({V_0} = V\left( {\left[ S \right] = 0} \right) = 0\)
\(\mathop {\lim }\limits_{\left[ S \right] \to + \infty } V = {V_{\max }}\)
\({V_{\max }}\) représente la vitesse maximale de réaction. Le graphe de \(V\) en fonction de \(\left[ S \right]\) présente une asymptote d’équation \(V = {V_{\max }}\).
\({K_M}\) est égal à la concentration en substrat correspond à une vitesse \(V = \frac{{{V_{\max }}}}{2}\) :
\(V\left( {\left[ S \right] = {K_M}} \right) = \frac{{{V_{\max }}}}{2}\)
\(V\) est continue et dérivable sur \(\left[ {0; + \infty } \right[\) :
\(V' = \frac{{dV}}{{d\left[ S \right]}} = \frac{{{V_{\max }}{K_M}}}{{{{\left( {{K_M} + \left[ S \right]} \right)}^2}}} > 0\)
La fonction \(V\) est strictement croissante sur \(\left[ {0; + \infty } \right[\) :
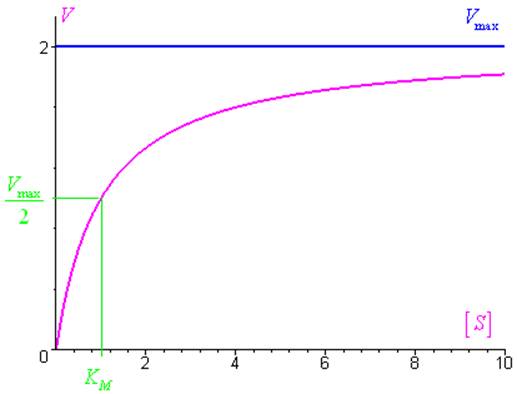
Unnamed Image
2 Fonctions trigonométriques et trigonométriques inverses
2.1 Définitions
On considère un repère orthonormé \(\left( {O,{{\vec e}_1},{{\vec e}_2}} \right)\), c’est-à-dire tel que \({\vec e_1} \bot {\vec e_2}\) et \(\left\| {{{\vec e}_1}} \right\| = \left\| {{{\vec e}_2}} \right\| = 1\).
Définitions 1 :
Le cercle trigonométrique est le cercle de centre \(O\) et de rayon 1 sur le quel on définit un sens de parcours.
Le sens est positif est le sens inverse des aiguilles d’une montre : on dit le sens trigonométrique direct.
Le sens est négatif est le sens des aiguilles d’une montre : c’est le sens trigonométrique indirect.
Remarque : Ces définitions ne sont en fait par rigoureuses au sens mathématique, puisque le sens trigonométrique direct ne peut en théorie être défini que dans \({\mathbb{R}^3}\).
Définition 2 :
Soit \(M\) un point du cercle trigonométrique. On appelle mesure en radians de l’angle \(\widehat {\left( {OI,OM} \right)}\), le réel \({\alpha _M}\) égal à la longueur de l’arc orienté (de \(I\) vers \(M\)).
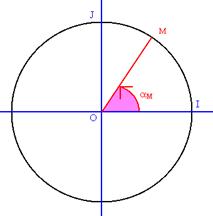
Unnamed Image
D’après le site de L. Garnier (Université de Bourgogne)
Remarque :
Si \(M\) et \(N\) ont même position sur le cercle trigonométrique, alors ${_M} = {_N} + 2k$ avec \(k \in \mathbb{Z}\).
Le graphe ci-dessous donne quelques valeurs remarquables d’angles :
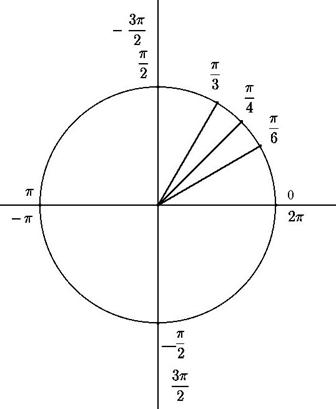
Unnamed Image
D’après le site de L. Garnier (Université de Bourgogne)
Définitions 3 :
Soit \(M\) un point du cercle trigonométrique.
On appelle sinus de l’angle \({\alpha _M}\) l’ordonnée du point \(M\).
On appelle cosinus de l’angle \({\alpha _M}\) l’abscisse du point \(M\).
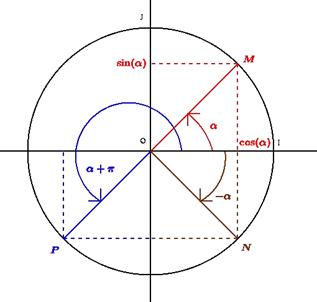
Unnamed Image
D’après le site de L. Garnier (Université de Bourgogne)
Pour tout angle $$, on a les relations suivantes (voir graphe ci-dessus) : *
\(\sin \alpha = \sin \left( {\alpha + 2k\pi } \right)\), \(k \in \mathbb{Z}\)
\(\cos \alpha = \cos \left( {\alpha + 2k\pi } \right)\), \(k \in \mathbb{Z}\)
$( { - } ) = - $
$( { - } ) = $
$( {+ } ) = - $
$( {+ } ) = - $
\({\cos ^2}\alpha + {\sin ^2}\alpha = 1\) *
Vous trouverez une liste d’autres relations dans l’aide mémoire « trigonométrie».
2.2 Fonctions trigonométriques
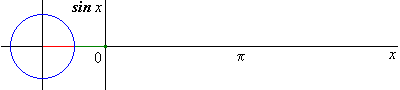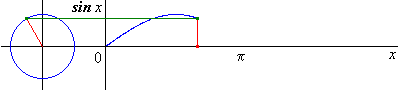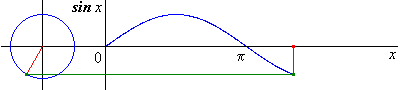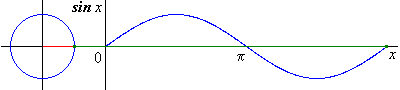
Fonction sinus
Du latin sinus = pli, cavité \(J\)
Elle est définie sur \(\mathbb{R}\) par \(f\left( * \right) = \sin x\)
Elle est impaire et $2$-périodique.
Elle est dérivable sur \(\mathbb{R}\) avec \({\left( {\sin } \right)^\prime }\left( x \right) = \cos x\).
Elle est strictement croissante sur \(\left[ {0;\frac{\pi }{2}} \right]\) et strictement décroissante sur \(\left[ {\frac{\pi }{2};\pi } \right]\).
Sa courbe est une sinusoïde ; elle est invariante par : * - les translations de vecteur \(2k\pi {\vec e_1}\) (puisqu’elle est $2$-périodique) * - les symétries de centres \(\left( {k\pi ,0} \right)\) (puisqu’elle est impaire) * - les symétries d’axes $x = + k$ *
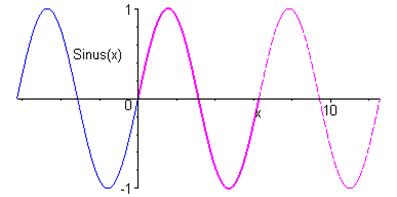
Unnamed Image
Version animée :
Fonction cosinus
du latin cum = avec donnant en français co = associé et sinus = pli
Elle est définie sur \(\mathbb{R}\) par \(f\left( * \right) = \cos x\)
Elle est paire et $2$-périodique.
Elle est dérivable sur \(\mathbb{R}\) avec \({\left( {\cos } \right)^\prime }\left( x \right) = - \sin x\).
Elle est strictement croissante sur \(\left[ { - \pi ;0} \right]\) et strictement décroissante sur \(\left[ {0;\pi } \right]\).
Sa courbe est une sinusoïde ; elle est invariante par : * - les translations de vecteur \(2k\pi {\vec e_1}\) * - les symétries de centres \(\left( {\frac{\pi }{2} + k\pi ,0} \right)\) * - les symétries d’axes $x = k$
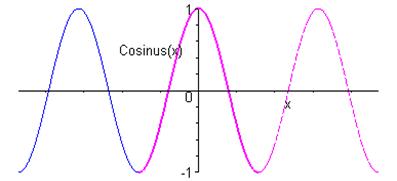
Unnamed Image
Fonction tangente
du latin tangere, tangentis = toucher
Elle est définie sur \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) par \(f\left( x \right) = \frac{{\sin x}}{{\cos x}} = \tan x\)
Elle est impaire et $$-périodique.
Elle est dérivable sur \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) avec \({\left( {\tan } \right)^\prime }\left( x \right) = 1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\).
Elle est strictement croissante sur \(\left] { - \frac{\pi }{2};\frac{\pi }{2}} \right[\)
Sa courbe est invariante par : * - les translations de vecteur \(k\pi {\vec e_1}\) * - les symétries de centres \(\left( {k\pi ,0} \right)\)
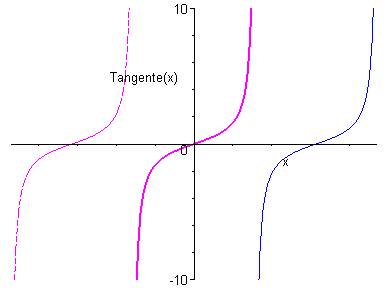 *
*
Fonction cotangente
du latin* cum = avec* donnant en français co = associé et tangente
Elle est définie sur \(\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\) par \(f\left( x \right) = \frac{{\cos x}}{{\sin x}} = \frac{1}{{\tan x}} = \cot x\)
Elle est impaire et $$-périodique.
Elle est dérivable sur \(\mathbb{R}\) avec \({\left( {\cot } \right)^\prime }\left( x \right) = - 1 - {\cot ^2}x = - \frac{1}{{{{\sin }^2}x}}\).
Elle est strictement décroissante sur \(\left] {0;\pi } \right[\)
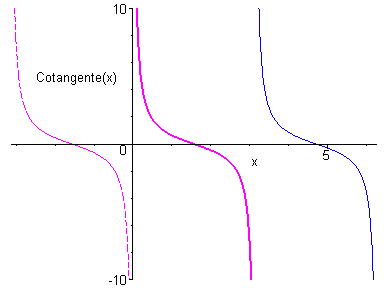
Unnamed Image
2.3 Fonctions trigonométriques inverses
La fonction sinus est bijective de tout intervalle \(\left[- \frac{\pi}{2} + 2k\pi ;\frac{\pi}{2} + 2k\pi \right] k \in \mathbb{Z}\) vers \(\left[ { - 1;1} \right]\) ; elle admet donc une fonction réciproque définie de \(\left[- 1;1 \right]\) vers \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\)
Ainsi, pour tout \(x \in \left[ { - 1;1} \right]\) il existe un unique \(y \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) tel que \(\sin y = x\).
Par définition, ce nombre \(y\) est appelé arc sinus \(x\), et noté \(y = \arcsin x\).
Fonction arcsinus
$ \begin{gathered} \arcsin :\left[ { - 1;1} \right] \to \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \hfill \\ \quad \quad \quad x \mapsto y = \arcsin x \hfill \\ \end{gathered}$
Elle est par construction définie, continue et impaire sur \(\left[- 1;1 \right]\).
Son graphe est symétrique de celui de sinus par symétrie par rapport à la première bissectrice.
Sa dérivée se calcule selon la règle établie au chapitre * §4.4 pour les fonctions réciproques : * \({\left( {\arcsin } \right)^\prime }\left( x \right) = \frac{1}{{\left( {\cos \circ \arcsin } \right)\left( x \right)}} = \frac{1}{{\cos y}} = \frac{1}{{\sqrt {1 - {{\sin }^2}y} }} = \frac{1}{{\sqrt {1 - {x^2}} }}\)
Elle est donc strictement croissante sur \(\left] { - 1;1} \right[\) avec deux tangentes verticales en \(1\) et \(- 1\).
Représentation graphique de la fonction arcsinus
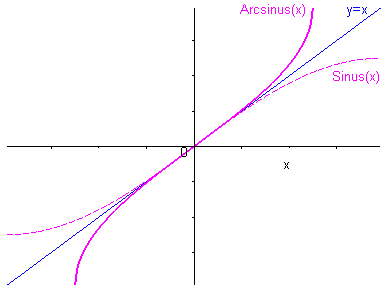 *
*
Fonction arccosinus
$ \begin{gathered} \arccos :\left[ { - 1;1} \right] \to \left[ {0;\pi } \right] \hfill \\ \quad \quad \quad x \mapsto y = \arccos x \hfill \\ \end{gathered}$ (par un raisonnement analogue au précédent)
Elle est définie, continue et paire sur \(\left[ { - 1;1} \right]\).
Son graphe se déduit de celui de cosinus par symétrie par rapport à la première bissectrice.
Sa dérivée se calcule comme précédemment : \({\left( {\arccos } \right)^\prime }\left( x \right) = - \frac{1}{{\sqrt {1 - {x^2}} }}\)
Elle est donc strictement décroissante sur \(\left] { - 1;1} \right[\) avec deux tangentes verticales en 1 et \(- 1\).
Représentation graphique de la fonction arccosinus
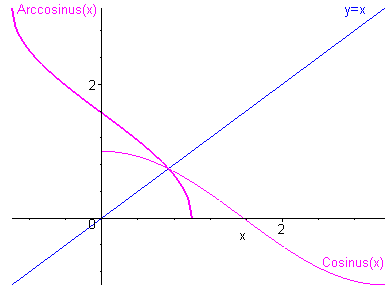 *
*
Fonction arctangente
$ \begin{gathered} \arctan :\left] { - \infty ; + \infty } \right[ \to \left] { - \frac{\pi }{2};\frac{\pi }{2}} \right[ \hfill \\ \quad \quad \quad x \mapsto y = \arctan x \hfill \\ \end{gathered}$
Elle est définie, continue et impaire sur \(\left] { - \infty ; + \infty } \right[\).
Son graphe se déduit de celui de tagente par symétrie par rapport à la première bissectrice.
Sa dérivée se calcule comme précédemment : * \({\left( {\arctan } \right)^\prime }\left( x \right) = \frac{1}{{1 + {x^2}}}\)
La fonction arctangente est donc strictement croissante sur \(\left] * - \infty ; + \infty \right[\).
Représentation graphique de la fonction arctangente
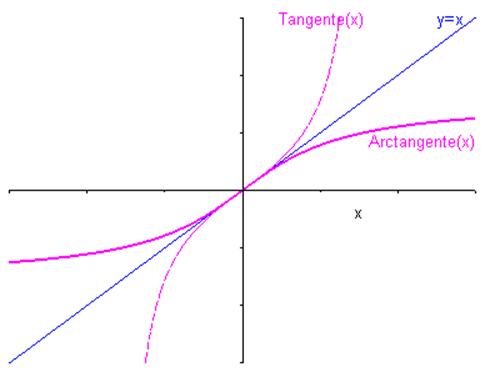
Unnamed Image
Relations fondamentales :
\(\arcsin x + \arccos x = \frac{\pi }{2}\)
\(\arctan x + {\text{arc}}\cot x = \frac{\pi }{2}\) avec \(y = {\text{arccot}}x \Leftrightarrow x = \cot y\quad y \in \left] {0,\pi } \right[\)
2.4 Les formules de Simpson (ou formules d’additions)
Les formules de Simpson et bien d’autres sont répertoriées dans le formulaire « trigonométrie» de la rubrique aide-mémoire. On les utilise pour transformer des sommes de sinus ou de cosinus en produits de sinus ou de cosinus. Ces formules trouvent des applications pour la calcul intégral (voir Chapitre 5).
Vers d’autres applications des formules de Simpson…
2.5 Généralisation
- l’aide des théorème de fonctions composées, il est facile d’obtenir les propriétés de fonctions s’écrivant comme combinaison des fonctions trigonométriques précédentes. Ainsi :
\({\left( {\sin \left[ {u(x)} \right]} \right)^\prime } = u'(x)\cos \left[ {u(x)} \right]\)
\({\left( {\cos \left[ {u(x)} \right]} \right)^\prime } = - u'(x)\sin \left[ {u(x)} \right]\)
\({\left( {\tan \left[ {u(x)} \right]} \right)^\prime } = \frac{{u'(x)}}{{{{\cos }^2}\left[ {u(x)} \right]}}\)
\({\left( {\cot \left[ {u(x)} \right]} \right)^\prime } = - \frac{{u'(x)}}{{{{\sin }^2}\left[ {u(x)} \right]}}\)
2.6 Un exemple d’application en Biologie
2.6.1 Le problème de la chèvre
2.6.2 La température de l’eau dans le Rhône
Les variations de température dans l’eau du Rhône sont cycliques, dépendent de la saison, et sont directement liées aux variations cycliques de la dureté de l’eau, mesurée en mg/L de CaC03 (carbonate de calcium).
Par exemple, on peut imaginer la relation suivante, si \(t\) désigne le temps et \(D\) la dureté de l’eau:
\(D = \alpha \cos \left( {\omega t + \varphi } \right) + \beta = f\left( t \right)\)
\(t\) est dite variable de contrôle (sa variation influence celle de \(D\)) ;
\(D\) est dite variable dépendent (ses variations dépendent de celles de \(t\)) ;
$,,,$ sont des paramètres, dont les valeurs dépendent de l’endroit et/ou du moment où sont mesurées les variations de \(D\). Les valeurs de ces paramètres peuvent aussi varier d’une année à l’autre, voire d’une saison à l’autre.
\(f\) est définie sur \(\mathbb{R}\) ; elle est $2$-périodique.
\(f'\left( t \right) = - \alpha \omega \sin \left( {\omega t + \varphi } \right)\)
La représentation graphique d’une telle fonction, pour des valeurs quelconques des paramètres $,,,$ est la suivante :
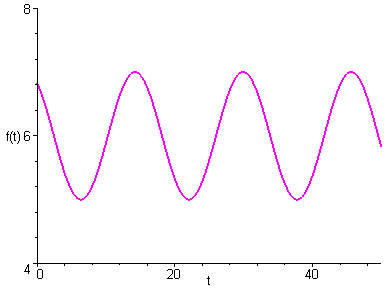
Unnamed Image
Des mesures de \(D\) ont été effectuées sur une durée totale d’un an (Carrel G., 1986) :
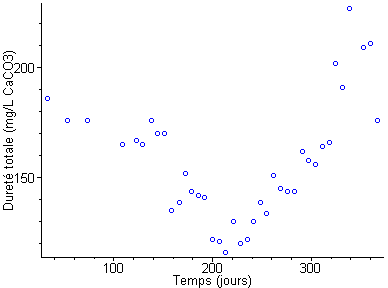
Unnamed Image
De telles mesures étant réalisées, il peut-être intéressant de savoir quelle fonction \(f\) permet de décrire l’évolution de la dureté de l’eau dans le temps. Il s’agit alors de trouver les valeurs des paramètres $,,,$ telles que la courbe représentative de \(D * f\left( t \right)\) passe « au mieux » entre les points. On parle dans ce cas d’ajustement d’une courbe (ou d’un modèle) à des données expérimentales.
Une telle analyse est possible à l’aide des logiciels Maple ou R et donne les résultats suivants :
\(\begin{gathered} \alpha = 34.24\\ \omega = 0.022\\ \varphi = - 1.71\\ \beta = 159.1\\ \end{gathered}\)
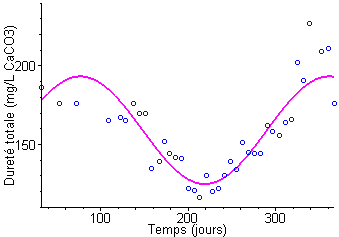
Unnamed Image
2.7 Vers d’autres sites…
15873: un site dédié aux mathématiques utilitaires de tous niveaux, sous forme d’exercices avec leurs solutions. Avec une partie “Aide Mémoire” (formulaire) pour les choses courantes.
Voir le formulaire trigo
3 Fonctions logarithme et exponentielle
3.1 Introduction
C’est dans le but de simplifier les calculs trigonométriques de l’astronomie que Neper invente les logarithmes (le terme est de lui, du grec logos * logique, raison et arithmos = nombre).
Il en expose le fonctionnement dans deux traités : Mirifici Logarithmorum Canonis Descriptio (1614), puis Mirifici Logarithmorum Canonis Constructio (posthume, 1619) soit : « Description (resp. Construction) de la Règle Admirable des Logarithmes ».
3.2 La fonction logarithme népérien
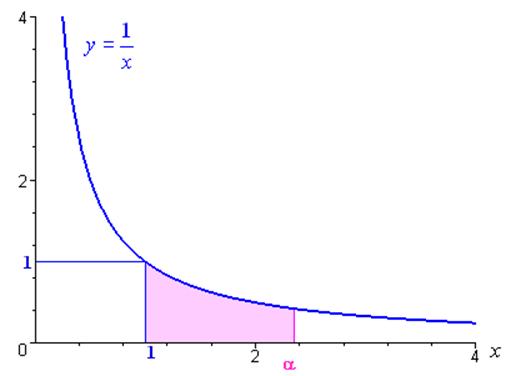
Comme la fonction \(x \mapsto \frac{1}{x}\) est dérivable sur \(\left] {0; + \infty } \right[\), elle admet une primitive sur cet intervalle (donc une infinité) ; en particulier on peut trouver une primitive qui s’annule en \(x = 1\).
Unnamed Image
Définition :
La fonction logarithme népérien, noté ln, est la primitive de la fonction \(x \mapsto \frac{1}{x}\) définit de \(\left] {0; + \infty } \right[\) sur \(\left] {0; + \infty } \right[\) et qui s’annule en \(x = 1\).
La fonction logarithme népérien est donc définie sur \(\left] {0; + \infty } \right[\) par \(\ln :x \mapsto \ln x\).
\(\ln 1 = 0\)
Pour tout \(\alpha \in \left] {0; + \infty } \right[\), l’aire du domaine délimité par l’axe des abscisses, la courbe \(y = \frac{1}{x}\) et les droites d’équation \(x = 1\) et $x = $ correspond exactement au calcul suivant :
$A = _1^ = _1^= $ si \(\alpha \geqslant 1\)
$A = ^1 {dx} = ^1 = - $ si \(0 < \alpha < 1\) Voir
Propriétés :
Pour tout \(a,b \in \left] {0; + \infty } \right[\) et pour tout \(p \in \mathbb{R}\), alors :
\(\ln \left( {ab} \right) = \ln a + \ln b\)
\(\ln \left( {\frac{1}{b}} \right) = - \ln b\)
\(\ln \left( {\frac{a}{b}} \right) = \ln a - \ln b\)
\(\ln \left( {{a^p}} \right) = p\ln a\)
La fonction ln est dérivable sur \(\left] {0; + \infty } \right[\) : \(\forall x > 0\), \({\left( {\ln } \right)^\prime }\left( x \right) = \frac{1}{x}\)
La fonction ln est strictement croissante sur \(\left] {0; + \infty } \right[\)
${x } x = - $ ${x + } x = + $ \(\mathop {\lim }\limits_{x \to 1} \frac{{\ln x}}{{x - 1}} = 1\) (par définition de la dérivée)
Unnamed Image
Aller vers… : Le point de vue géométrique de X. Hubaut est une autre façon de retenir la définition de la fonction logarithme népérien.
La fonction \(lnou\)*** : ***\({\left( {\ln \circ u} \right)^\prime }\left( x \right) = \frac{{u'\left( x \right)}}{{u\left( x \right)}}\)
3.3 La fonction exponentielle
Théorème :
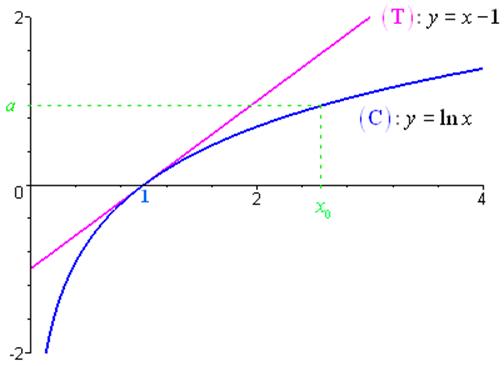
La fonction ln réalise une bijection strictement croissante de \(\left] {0; + \infty } \right[\) sur \(\mathbb{R}\).
Par conséquent, \(\forall a \in \mathbb{R}\), l’équation \(\ln x = a\) admet une unique solution \({x_0} \in \left] {0; + \infty } \right[\) (voir figure ci-dessus).
En particulier, si on prend \(a = 1\), on appelle \(e\) l’unique réel strictement positif dont le logarithme népérien vaut 1 : \(\ln * = 1\).
Conséquence :
L’équation \(\ln x = a\) admet une unique solution \({x_0} = {e^a}\). En effet : \(\ln \left( {{e^a}} \right) = a\ln e = a\).
Définition :
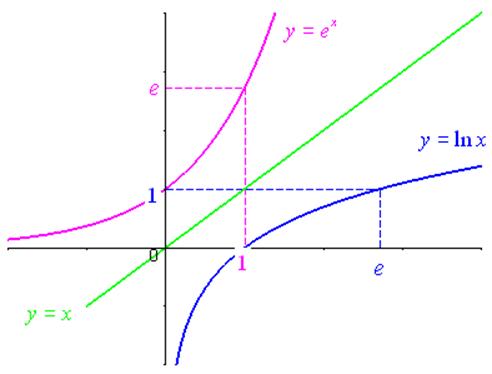
La fonction exponentielle est la bijection réciproque de la fonction ln. On la note :
\(e:x \mapsto {e^x}{\text{ ou }}\exp \left( x \right)\)
La fonction exponentielle est définie sur \(\mathbb{R}\).
\(\forall x \in \mathbb{R}\), \({e^x} > 0\)
\(\forall x \in \mathbb{R}\) et \(\forall y \in \left] {0; + \infty } \right[\) : \({e^x} = y \Leftrightarrow x = \ln y\)
\(\ln \left( {{e^x}} \right) = x\) \({e^{\ln y}} = y\)
Propriétés :
Pour tout \(a,b \in \mathbb{R}\) et pour tout \(p \in \mathbb{R}\), alors :
\({e^{a + b}} = {e^a}{e^b}\)
\({e^{ - b}} = \frac{1}{{{e^b}}}\)
\({e^{a - b}} = \frac{{{e^a}}}{{{e^b}}}\)
\({\left( {{e^a}} \right)^p} = {e^{ap}}\)
Exemple :\(\frac{{{e^{4x - 1}}}}{{{e^{x + 3}}}} * {e^{4x - 1 - x - 3}} = {e^{3x - 4}}\)
La fonction exponentielle est dérivable sur \(\mathbb{R}\) : \({\left( {\exp } \right)^\prime }\left( x \right) = \exp \left( x \right)\)
La fonction exponentielle est strictement croissante de \(\mathbb{R}\) sur \(\left] {0; + \infty } \right[\)
\(\mathop {\lim }\limits_{x \to - \infty } {e^x} = {0^ + }\) ${x + } {e^x} = + $ ${x + } = + $
Unnamed Image
La fonction \(exp\;o\;u\) : \({\left( {\exp \circ u} \right)^\prime }\left( x \right) = u'\left( x \right)\left( {\exp \circ u} \right)\left( x \right) \Leftrightarrow {\left( {{e^u}} \right)^\prime } = u'{e^u}\).
3.4 Exemples d’utilisation en Biologie
3.4.1 La fonction exponentielle
L’exemple qui suit est extrait de Lomen et Lovelock, 1999, p51.
Pendant la première moitié du 20ème siècle, les populations de tourterelles turques (« collared dove ») envahissent l’Europe d’Est en Ouest. Cet oiseau était très rare en Grande-Bretagne avant1955. L’invasion de cette espèce en Grande-Bretagne est d’un intérêt tout particulier pour les ornithologues ce qui les a conduit à faire des recensements de populations réguliers entre 1955 et 1964.
On peut raisonnablement supposer que le nombre de tourterelles turques est proportionnel au nombre d’endroit où l’espèce est recensée. Ainsi, les relevés ornithologiques de l’époque fournissent les données suivantes :
| Temps (année) | Nombre de lieux recensés |
|---|---|
| 1955 | 1 |
| 1956 | 2 |
| 1957 | 6 |
| 1958 | 15 |
| 1959 | 29 |
| 1960 | 58 |
| 1961 | 117 |
| 1962 | 204 |
| 1963 | 342 |
| 1964 | 501 |
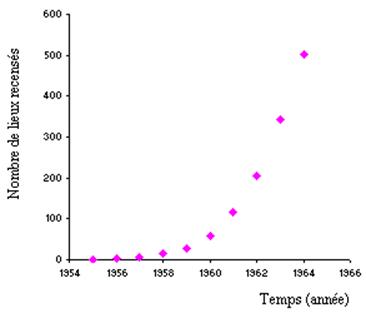
Unnamed Image
\(N = \alpha {e^{\beta t}}\)
Si \(t\) désigne l’année et \(N\) le nombre de lieux où la tourterelle turque a été recensée. Les paramètres $,$ sont choisis pour décrire « au mieux » la série de données.
Une transformation logarithmique permet d’écrire :
\(\ln N = \ln \alpha + \beta \ln t\)
Ainsi, la représentation de \(\ln N\) en fonction de \(t\) est une droite, ce que permet de vérifier le graphe ci-dessous :
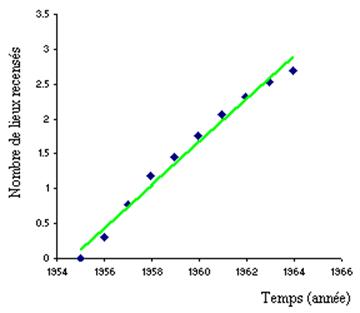
Unnamed Image
3.4.2 La fonction logistique
L’exemple qui suit est extrait de Lomen et Lovelock, 1999, p42. *
Dans le tableau ci-dessous, on peut voir l’évolution dans le temps de la taille moyenne d’un plan de tournesol :
| Temps (jours) | Taille (cm) |
|---|---|
| 7 | 17.93 |
| 14 | 36.36 |
| 21 | 67.76 |
| 28 | 98.10 |
| 35 | 131 |
| 42 | 169.50 |
| 49 | 205.50 |
| 56 | 228.30 |
| 63 | 247.10 |
| 70 | 250.50 |
| 77 | 253.80 |
| 84 | 254.50 |
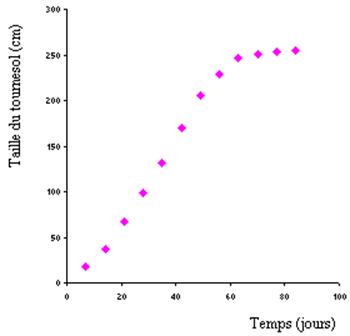
Unnamed Image
On constate que pour de faibles valeurs du temps, la taille augmente de façon linéaire, puis que pour des temps plus important la croissance ralentit.
La fonction logistique est la plus classique pour décrire ce genre de données expérimentales.
Si on désigne par \(T\) la taille du plan de tournesol et par \(t\) le temps, on peut alors écrire :
\(T(t) =\frac{T_0}{(1-T_0/\alpha)e^{-\alpha \beta t}+T_0/\alpha}\)
En choisissant au mieux les valeurs des paramètres \(\alpha ,\beta ,{T_0}\), on peut construire la courbe qui « passe au mieux » entre les points expérimentaux :
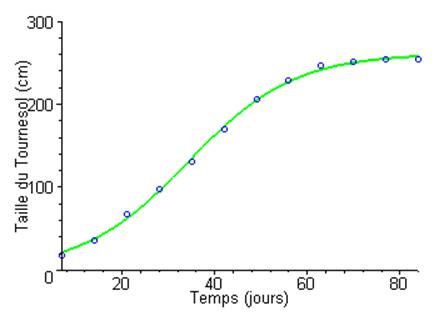
Unnamed Image
4 Fonctions hyperboliques et hyperboliques inverses
4.1 Définition des fonctions hyperboliques
Par définition, on appelle cosinus hyperbolique de \(x\), la quantité notée \(\operatorname{ch} x\) :
\(\operatorname{ch} x = \frac{{{e^x} + {e^{ - x}}}}{2}\)
De la même manière, on définit le sinus hyperbolique, notée \(\operatorname{sh} x\) :
\(\operatorname{sh} x = \frac{{{e^x} - {e^{ - x}}}}{2}\)
On constate que \(\operatorname{ch} x + \operatorname{sh} x = {e^x}\) et que \(\operatorname{ch} * - \operatorname{sh} x = {e^{ - x}}\). Il vient alors immédiatement :
\({\operatorname{ch} ^2}x - {\operatorname{sh} ^2}x = 1\) (1)
Par analogie avec les fonctions trigonométriques, on définit la tangente hyperbolique, notée \(\operatorname{th} x\) (ou bien \(\tanh x\)) par :
\(\operatorname{th} x = \frac{{\operatorname{sh} x}}{{\operatorname{ch} x}} = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} * \frac{{{e^{2x}} - 1}}{{{e^{2x}} + 1}}\)
On utilise quelquefois la co-tangente hyperbolique, notée \(\coth x\), et définie par :
\(\coth x = \frac{1}{{\operatorname{th} x}} = \frac{{\operatorname{sh} x}}{{\operatorname{ch} x}}\)
Les deux relations suivantes découlent immédiatement de la relation (1) :
\(\frac{1}{{{{\operatorname{ch} }^2}x}} = 1 - {\operatorname{th} ^2}x\) \(\frac{1}{{{{\operatorname{sh} }^2}x}} = {\coth ^2}x - 1\)
4.2 Etude des fonctions hyperboliques
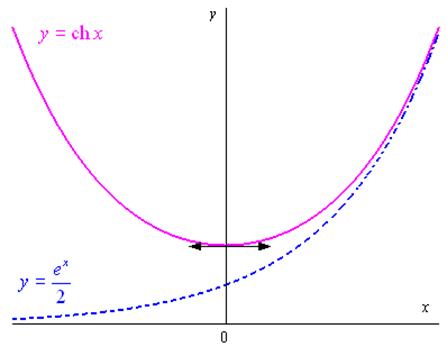
4.2.1 Etude de la fonction \(f\left( x \right) = chx\)
\(\operatorname{ch} x = \frac{{{e^x} + {e^{ - x}}}}{2}\) \(D = \mathbb{R}\)
\(\operatorname{ch} \left( { - x} \right) = \operatorname{ch} x\)
La fonction paire : on fait l’étude sur \({\mathbb{R}^ * }\) et le graphe est symétrique par rapport à \(\left( {Oy} \right)\).
\(\operatorname{ch} 0 = 1\)
$_{x + } * = + $
\({\left( {\operatorname{ch} x} \right)^\prime } = \operatorname{sh} x\) : la fonction est strictement croissante sur \({\mathbb{R}^ * }\)
Unnamed Image
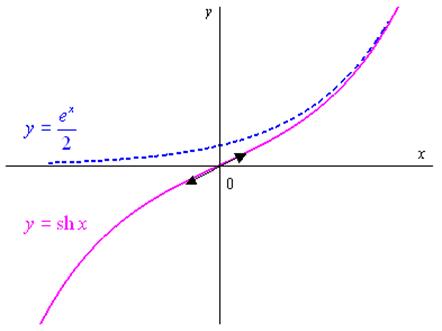
4.2.2 Etude de la fonction \(f\left( x \right) = shx\)
\(\operatorname{sh} x = \frac{{{e^x} - {e^{ - x}}}}{2}\) \(D = \mathbb{R}\)
\(\operatorname{sh} \left( { - x} \right) = - \operatorname{sh} x\)
La fonction impaire : on fait l’étude sur \({\mathbb{R}^ * }\) et le graphe est symétrique par rapport à l’origine.
\(\operatorname{sh} 0 = 0\)
$_{x + } * = + $
\({\left( {\operatorname{sh} x} \right)^\prime } = \operatorname{ch} x\) : la fonction est strictement croissante sur \({\mathbb{R}^ * }\)
Unnamed Image
Remarque : \({\left( {\operatorname{sh} } \right)^\prime }\left( 0 \right) = 1\) entraîne que \(\mathop {\lim }\limits_{x \to 0} \frac{{\operatorname{sh} x}}{x} = 1\).
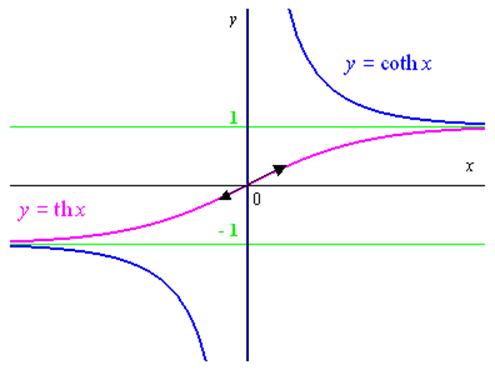
4.2.3 Etude de la fonction \(f\left( x \right) = thx\)
\(\operatorname{th} x = \frac{{\operatorname{sh} x}}{{\operatorname{ch} x}} = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} * \frac{{{e^{2x}} - 1}}{{{e^{2x}} + 1}}\) \(D = \mathbb{R}\)
\(\operatorname{th} \left( { - x} \right) = - \operatorname{th} x\)
La fonction impaire : on fait l’étude sur \({\mathbb{R}^ * }\) et le graphe est symétrique par rapport à l’origine.
\(\operatorname{th} 0 = 0\)
\(\mathop {\lim }\limits_{x \to + \infty } \operatorname{th} * = 1\)
La droite \(y = 1\) est asymptote en $ + $
\({\left( {\operatorname{th} x} \right)^\prime } = \frac{1}{{{{\operatorname{ch} }^2}x}} > 0\) : la fonction est strictement croissante sur \({\mathbb{R}^ + }\)
Unnamed Image
Remarque : \(\mathop {\lim }\limits_{x \to 0} \frac{{\operatorname{th} x}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{{\operatorname{ch} x}}\frac{{\operatorname{sh} x}}{x}} \right) = 1\).
4.3 Formules usuelles
Dans la rubrique aides-mémoire, vous trouverez un formulaire récapitulatif des formules usuelles impliquant les fonctions hyperboliques.
4.4 Définition des fonctions hyperboliques réciproques
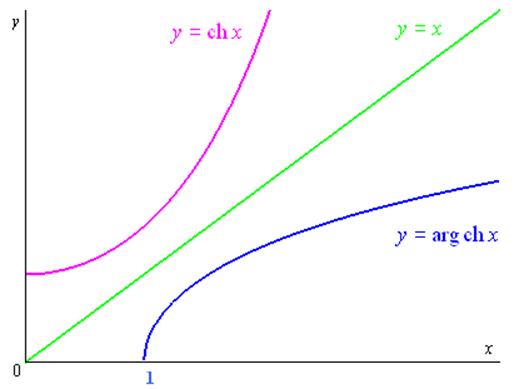
4.4.1 Définition de la fonction réciproque du cosinus hyperbolique
Définition :
La fonction réciproque du cosinus hyperbolique se note \(\arg \operatorname{ch} x\) et se définit par :
\(\left. \begin{gathered} y = \arg \operatorname{ch} x \hfill \\ {\text{avec }}x \geqslant 1 \hfill \\ \end{gathered} \right\} \Leftrightarrow \left\{ \begin{gathered} x = \operatorname{ch} y \hfill \\ {\text{avec }}y \geqslant 0 \hfill \\ \end{gathered} \right.\)
\(\arg \operatorname{ch} x\) est une fonction continue, croissante et bijective de \(\left[ {1; + \infty } \right[\) sur \(\left[ {0; + \infty } \right[\).
\({\left( {\arg \operatorname{ch} x} \right)^\prime } = \frac{1}{{\sqrt {{x^2} - 1} }}\)
Unnamed Image
Expression logarithmique de \(argchx\)
De la définition précédente, il vient \(2x = {e^y} + {e^{ - y}}\). Si on pose \(Y = {e^y}\), alors \({Y^2} * 2xY + 1 = 0\), ce qui conduit par résolution de cette équation du second degré à $Y = x + $. Ainsi :
\(\arg \operatorname{ch} x = \ln \left( {x + \sqrt {{x^2} - 1} } \right)\)
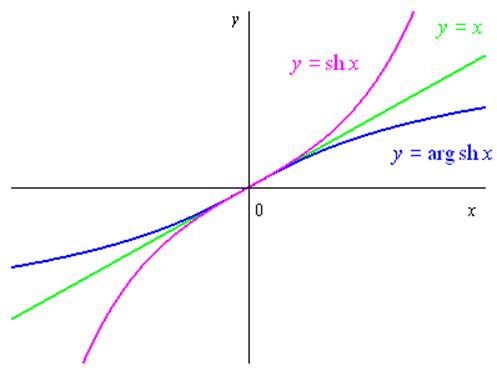
4.4.2 Définition de la fonction réciproque du sinus hyperbolique
Définition :
La fonction réciproque du sinus hyperbolique se note \(\arg \operatorname{sh} x\) et se définit par :
\(y = \arg \operatorname{sh} x \Leftrightarrow x = \operatorname{sh} y\) pour tout \(x \in \mathbb{R}\)
\(\arg \operatorname{sh} x\) est une fonction continue, croissante et bijective de \(\mathbb{R}\) sur \(\mathbb{R}\).
\({\left( {\arg \operatorname{sh} x} \right)^\prime } = \frac{1}{{\sqrt {{x^2} + 1} }}\)
Unnamed Image
Expression logarithmique de \(argshx\)
De la définition précédente, il vient \(2x = {e^y} - {e^{ - y}}\). Si on pose \(Y = {e^y}\), alors \({Y^2} * 2xY - 1 = 0\), ce qui conduit par résolution de cette équation du second degré à $Y = x + $. Ainsi :
\(\arg \operatorname{sh} x = \ln \left( {x + \sqrt {{x^2} + 1} } \right)\)
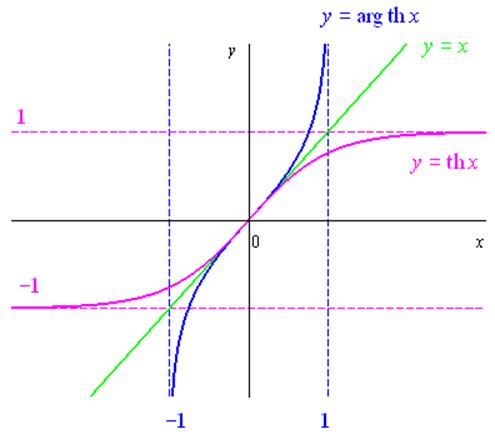
4.4.3 Définition de la fonction réciproque de la tangente hyperbolique
Définition :
La fonction réciproque du tangente hyperbolique se note \(\arg \operatorname{th} x\) et se définit par :
\(\left. \begin{gathered} y = \arg \operatorname{th} x \hfill \\ {\text{avec }} - 1 < x < 1 \hfill \\ \end{gathered} \right\} \Leftrightarrow x = \operatorname{th} y\)
\({\left( {\arg \operatorname{th} x} \right)^\prime } = \frac{1}{{1 - {x^2}}}\)
Unnamed Image
Expression logarithmique de \(argthx\)
Par une démarche analogue aux précédente, on obtient :
\(\arg \operatorname{th} x = \frac{1}{2}\ln \left( {\frac{{1 + x}}{{1 - x}}} \right)\)
5 Fonctions puissances
5.1 Définition
Définition :
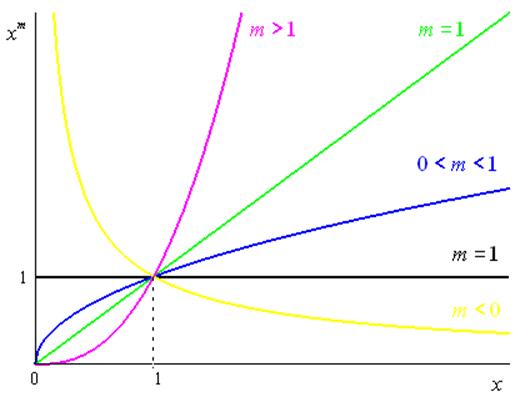
Une fonction puissance est une fonction dépendant d’un paramètre réel quelconque \(m \ne 0\) et définie sur \({\mathbb{R}^{ + * }}\) par :
\({f_m}\left( x \right) = {x^m} = {e^{m\ln x}}\)
L’étude des limites aux bornes de l’intervalle de définition dépende du signe de \(m\) :
Si \(m > 0\), alors \(\mathop {\lim }\limits_{x \to {0^ + }} {x^m} = 0\) et $_{x + } {x^m} = + $
Si \(m < 0\), alors $_{x } {x^m} = + $ et \(\mathop {\lim }\limits_{x \to + \infty } {x^m} = 0\)
Une fonction puissance est définie, continue et dérivable pour tout \(x > 0\) :
\({\left( {{f_m}} \right)^\prime }\left( x \right) = m{x^{m - 1}}\)
Ainsi, les variations de la fonction puissance dépendent du signe de \(m\) :
Unnamed Image
Propriété :
\({\left( {{x_1}{x_2}} \right)^m} = x_1^mx_2^m\)
5.2 Fonction um
Définition :
\(m\) étant un réel et \(u\) une fonction définie et strictement positive sur une partie \(D \subseteq \mathbb{R}\), la fonction \({u^m}\) est définie sur \(D\) par :
\({u^m}\left( x \right) = {\left( {u\left( x \right)} \right)^m}\)
D’après le théorème de dérivation d’une fonction composée (Chapitre 3, § 4.3), il vient :
Proposition :
\(m\) étant un réel et \(u\) une fonction dérivable et strictement positive sur un intervalle \(I\) de \(\mathbb{R}\), alors la fonction \({u^m}\) est dérivable sur \(I\) et : * \({\left( {{u^m}} \right)^\prime } = m\;u'\;{u^{m - 1}}\)
Cas particulier :
Soient \(m \in \mathbb{R}\) et \(f\) une fonction définie sur \(\left] { - 1; + \infty } \right[\) par \(f\left( x \right) = {\left( {1 + x} \right)^m}\) : \(f\left( * \right) = 1\).
\(f\) est dérivable sur \(\left] { - 1; + \infty } \right[\) et \(f'\left( x \right) = m{\left( {1 + x} \right)^{m - 1}}\) avec \(f'\left( 0 \right) = m\). Ainsi, par définition de la dérivabilité de \(f\) en 0, on obtient :
\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\left( {1 + x} \right)}^m} - 1}}{x} = m\)
Ceci peut encore s’écrire \({\left( {1 + x} \right)^m} = 1 + mx * x\varepsilon \left( x \right)\) avec \(\mathop {\lim }\limits_{x \to 0} \varepsilon \left( x \right) = 0\).
La fonction \(x \mapsto 1 + mx\) constitue donc une approximation affine de la fonction \(x \mapsto {\left( {1 + x} \right)^m}\) au voisinage de 0.
Proposition :
\(m\) étant un réel $ 1$ et \(u\) une fonction dérivable et strictement positive sur un intervalle \(I\) de \(\mathbb{R}\), alors la fonction \(u'\;{u^m}\) admet pour primitive sur \(I\) la fonctiont : * \(\frac{1}{{m * 1}}{u^{m + 1}}\)
5.3 Croissances comparées
Théorème :
Si \(m > 0\), alors \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\ln x}}{{{x^m}}} = 0\) et $_{x + } = + $
Si \(m < 0\), alors ${x + } = + $ et ${x + } = + $
Remarque :
Pour \(x > 0\), en écrivant \({x^m}{e^{ * x}} = \frac{{{x^m}}}{{{e^x}}}\), on obtient si \(m > 0\) :
\(\mathop {\lim }\limits_{x \to + \infty } {x^m}{e^{ - x}} = 0\)
5.4 Un exemple d’application en Biologie : la relation allométrique
L’allométrie est l’étude des tailles relatives des différentes parties d’un organisme, sous l’influence de la croissance. Classiquement, on cherche à relier la taille et le poids d’un individu.
On doit à Huxley (1932) la relation (ou équation) allométrique de base :
\(Y = \alpha {X^\beta }\)
où \(X\) représente par exemple le poids et \(Y\) la taille. $$ et $$ sont deux paramètres réels dont la valeur va dépendre de l’espèce étudiée.
L’intérêt de cette relation est que l’on peut la linéariser :
\(Y = \alpha {X^\beta } \Leftrightarrow \ln Y = \alpha + \beta \ln X\)
Ainsi, vous verrez dans votre cours de Probabilités – Statistiques en 2ème année de Deug SV, comment on peut obtenir des estimations des paramètres $$ et $$ à partir d’un jeu de données expérimentales.
Huxley donne l’exemple de la relation qui existe entre le poids des pinces de crabes (« fiddler-crab » et leur masse corporelle.
Voici une représentation graphique des données expérimentales brutes :
Voici une représentation graphique des données transformées en logarithme népérien :
La droite bleue permet de vérifier la linéarité de la relation entre les deux grandeurs, poids des pinces de homard, et masse corporelle, en coordonnées logarithme népérien.
 D’après
D’après