Chapitre 3 — Variables aléatoires
1. Introduction
Dans la plupart des phénomènes aléatoires, le résultat d’une épreuve peut se traduire par une « grandeur » mathématique, très souvent représentée par un nombre entier ou un nombre réel. La notion mathématique qui représente efficacement ce genre de situation concrète est celle de variable aléatoire (notée également v.a.). Ainsi le temps de désintégration d’un atome radioactif, le pourcentage de réponses « oui » à une question posée dans un sondage ou le nombre d’enfants d’un couple sont des exemples de variables aléatoires.
Remarque : On se limitera ici au cas des variables aléatoires réelles (les entiers faisant bien sûr partie des réels).
Etant donné un espace probabilisé d’espace fondamental \(\Omega\) et de mesure de probabilité \(P\), on appelle variable aléatoire sur cet espace, toute application \(X\) de \(\Omega\) dans \(\mathbb{R}\) telle que :
\(X : \varepsilon(\Omega) \longrightarrow F\)
\(\omega \longmapsto X(\omega)\)
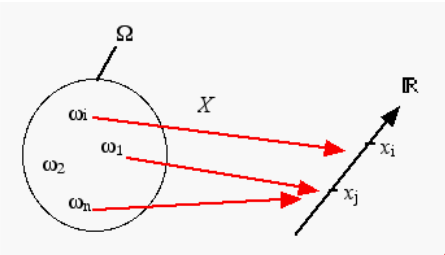
A chaque évènement élémentaire \(\omega\) de \(\Omega\) correspond un nombre réel \(x\) associé à la variable aléatoire \(X\). Comme l’indique le graphe, il n’y a pas obligatoirement autant de valeurs possibles prises par la variable aléatoire \(X\) que d’évènements élémentaires. La valeur \(x\) correspond à la réalisation de la variable \(X\) pour l’évènement élémentaire \(\omega\).
Exemple:
Si l’on considère la constitution d’une fratrie de deux enfants, l’espace fondamental est constitué des évènements élémentaires suivant :
\(\Omega = \{GG, GF, FG, FF\}\)
Les valeurs possibles prises par la variable aléatoire \(X\), « nombres de fille dans la famille » sont : \(X (\Omega) = \{0, 1, 2\}\)
2 Variables aléatoires discrètes
2.1 Définition
Une variable aléatoire est dite discrète si elle ne prend que des valeurs discontinues dans un intervalle donné (borné ou non borné). L’ensemble des nombres entiers est discret. En règle générale, toutes les variables qui résultent d’un dénombrement ou d’une numération sont de type discrètes.
Exemples :
Les variables aléatoires,
le nombre de petits par porté pour une espèce animale donnée (chat, marmotte, etc),
le nombre de bactéries dans 100 ml de préparation,
le nombre de mutations dans une séquence d’ADN de 10 kb,
etc…
sont des variables aléatoires discrètes.
2.2 Loi de probabilité
Une variable aléatoire est caractérisée par l’ensemble des valeurs qu’elle peut prendre et par l’expression mathématique de la probabilité de ces valeurs. Cette expression s’appelle la loi de probabilité (ou distribution de probabilité) de la variable aléatoire.
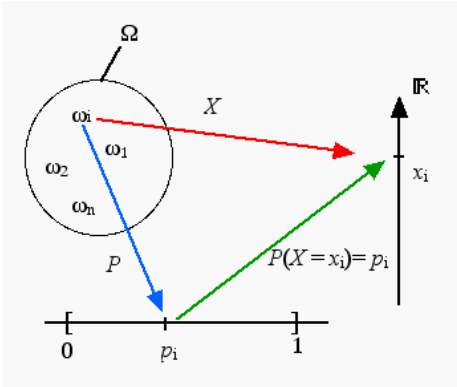
La loi de probabilité d’une variable aléatoire discrète est entièrement déterminée par les probabilités \(p_i\) des évènements \({X = x_i }\) , \(x_i\) parcourant l’univers image \(X(\Omega)\). La loi de probabilité est donnée par les \((x_i , p_i)_ {i}\) .
Remarque :
Afin de simplifier l’écriture, nous noterons pour la suite du cours :
\(P(\{X = x_i \})\) équivalent à \(P(X=x_i )\) ou \(p_i\)
Exemple :
Dans le cas de la constitution d’une fratrie de deux enfants, si l’on fait l’hypothèse que la probabilité d’avoir un garçon est égale à celle d’avoir une fille (1/2), alors la distribution de probabilité ou loi de probabilité du nombre de filles dans une fratrie de deux enfants est :

Si \(P(F) = P(G) = 1/2\), alors
- \(P[(F\cap G)\cup (G\cap F)] = P(F\cap G) + P(G\cap F)\) Propriétés d’additivité
avec \((F\cap G) \cap (G\cap F)=\emptyset\) évènements incompatibles
- \(P(F\cap G)= P(F)P(G)\) Propriété d’indépendance
d’où \(P[(F\cap G)\cup (G\cap F)]= P(X =1)= (1/2 \times 1/2)+(1/2 \times 1/2)=1/2\)
Remarque :
Une loi de probabilité n’est établie que si \(\sum\limits_i {p_i} = 1\), la somme étant étendue à tous les indices \(i\).
2.3 Fonction de répartition
On appelle fonction de répartition d’une variable aléatoire \(X\), la fonction \(F_X\) telle que :
\(F_X : \mathbb{R} \longrightarrow \mathbb{R}\)
\(t \longmapsto F_X (t) = P(X < t)\)
Concrètement la fonction de répartition correspond à la distribution des probabilités cumulées. Le plateau atteint par la fonction de répartition correspond à la valeur de probabilité 1 car \(\sum\limits_i {p_i} = 1\).
L’importance pratique de la fonction de répartition est qu’elle permet de calculer la probabilité de tout intervalle dans \(\mathbb{R}\).
Les propriétés associées à la fonction de répartition sont les suivantes :
Soit \(F_X\) la fonction de répartition d’une variable aléatoire discrète \(X\) alors :
(\(P_1\)) \(\forall t \in \mathbb{R} \quad 0 \leq F_X \quad (t) \leq 1\)
(\(P_2\)) \(F_X\) est croissante sur \(\mathbb{R}\)
(\(P_3\)) \(\lim\limits_{t \to - \infty } F_X (t) = 0 \quad \text{et} \quad \lim\limits_{t \to + \infty } F_X (t) = 1\)
(\(P_4\)) si \(a \leq b \qquad P (a \leq X \leq b) = F_X (b) - F_X (a)\)
Voici pourquoi :
(\(P_1\)) résulte de la définition d’une probabilité
(\(P_2\)) si \(a \leq b\), alors \(\{X < a \} \subset \{X < b \}\) donc \(P(X < a ) \leq P(X < b )\) (voir inclusion)
(\(P_3\)) même raison que pour \(P_1\)
(\(P_4\)) \(\{X < b \} = \{ a \leq X \leq b \} \cup \{X < a \}\) ainsi \(F_X (b) = P(a \leq X \leq b) + F_X (a)\)
Exemple :
On considère l’évènement \(\omega\) « lancer de 3 pièces ». On introduit une variable aléatoire \(X\) définie par \(X(\omega)\) « nombre de piles de l’évènement \(\omega\)». La loi de probabilité de \(X\) est :

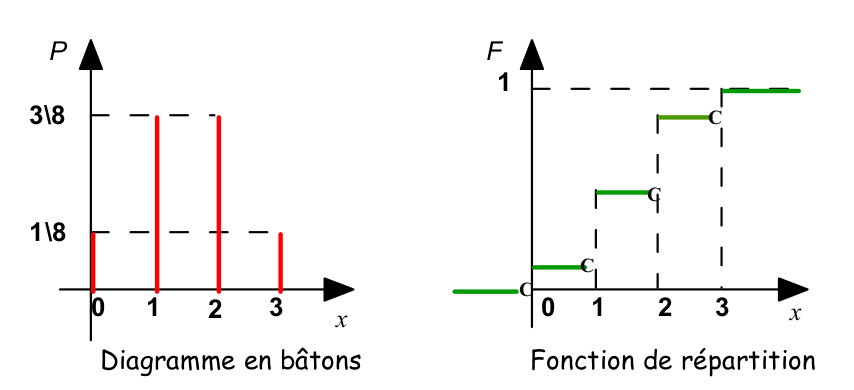
Dans le cas d’une variable aléatoire discrète, on utilise un diagramme en bâtons pour visualiser la distribution de probabilités et une fonction escalier pour la fonction de répartition
3 Variables aléatoires continues
3.1. Définition
Une variable aléatoire est dite continue si elle peut prendre toutes les valeurs dans un intervalle donné (borné ou non borné). En règle générale, toutes les variables qui résultent d’une mesure sont de type continu.
Exemples:
Les variables aléatoires,
le masse corporelle des individus pour une espèce animale donnée,
taux de glucose dans le sang,
etc.
sont des variables aléatoires continues.
3.2. Fonction densité de probabilité
Dans le cas d’une variable aléatoire continue, la loi de probabilité associe une probabilité à chaque ensemble de valeurs définies dans un intervalle donné. En effet, pour une variable aléatoire continue, la probabilité associée à l’évènement \(\{ X = a\}\) est nulle, car il est impossible d’observer exactement cette valeur.
On considère alors la probabilité que la variable aléatoire \(X\) prenne des valeurs comprises dans un intervalle \([a,b]\) tel que \(P(a \leq X \leq b)\).
Lorsque cet intervalle tend vers 0, la valeur prise par \(X\) tend alors vers une fonction que l’on appelle fonction densité de probabilité ou densité de probabilité.
On appelle densité de probabilité toute application continue par morceaux :
\(f : \mathbb{R} \longrightarrow \mathbb{R}\)
\(x \longmapsto f(x) = x\)
telle que :
(\(P_1\)) \(\forall x \in \mathbb{R} \qquad f(x) \geq 0\)
(\(P_2\)) \(\int_{- \infty}^{ + \infty } f(x) dx = 1\) (en supposant que \(\int_{- \infty}^{ + \infty } f(x) dx\) existe)
Soit une fonction densité de probabilité \(f(x)\) :
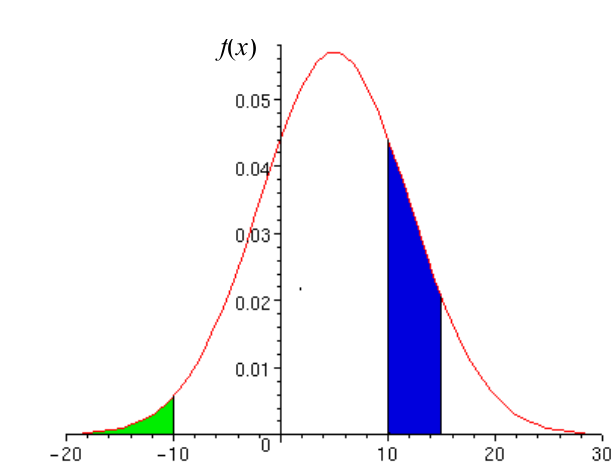
l’aire hachurée en vert correspond à la probabilité \(P(X < -10)\)
l’aire hachurée en bleu correspond à la probabilité \(P(+10 <X < +15)\)
Remarque :
Cette fonction densité de probabilité est une loi de probabilité car l’aire sous la courbe est égale à 1 pour toutes les valeurs de \(x\) définies.
Réciproquement :
Une variable aléatoire \(X\) définie sur un univers \(\Omega\) est dite absolument continue, s’il existe une fonction densité de probabilité \(f\) telle que :
\(\forall t \in \mathbb{R} \qquad P(X < t) = \int_{- \infty}^{ t } f(x) dx\)
(voir graphe ci-dessus).
3.3. Fonction de répartition
Si comme pour les variables aléatoires discrètes, on définit la fonction de répartition de \(X\) par :
\(F_X : \mathbb{R} \longrightarrow \mathbb{R}\)
\(t \longmapsto F_X(t) = P( X < t)\)
alors la relation entre la fonction de répartition \({F_X}\) et la fonction densité de probabilité f(x) est la suivante :
\(\forall t \in \mathbb{R} \qquad F_X (t) = P( X < t) = \int_{- \infty}^{ t } f(x) dx\)
La fonction de répartition \(F_X (t)\) est la primitive (voir cours d’analyse) de la fonction densité de probabilité \(f(x)\), et permet d’obtenir les probabilités associées à la variable aléatoire \(X\), en effet :
Soit \(X\) une variable aléatoire absolument continue de densité \(f\) et de fonction de répartition \(F_X\) , alors :
(\(P_1\)) \(P(a \leq X \leq b) = F_X (b) - F_X (a) = \int_{a}^{b} f(x) dx\) avec \(a < b\)
(\(P_2\)) \(\forall a \in \mathbb{R} \qquad P(x = a) = 0\) si f est continue à droite du point \(a\).
Voici pourquoi :
(\(P_1\)) \(P(a \leq X \leq b) = P(X < b) - P(X < a) = F_X (b) - F_X (a)\)
d’où \({\int_{- \infty}^{ b } f(x) dx} - {\int_{- \infty}^{ a } f(x) dx} = {\int_{a}^{b} f(x) dx}\)
(\(P_2\)) Si \(f\) est continue sur un intervalle de la forme \([a, a+h]\) avec \(h \longrightarrow 0^+\) alors,
\(P(a \leq X \leq a+h) = {\int_{a}^{a+h} f(x) dx} = h f (a + \theta h)\) avec \((0 < \theta <1)\); (théorème des accroissements finis)
Ainsi lorsque \(h \longrightarrow 0 : f (a+ \theta h) \longrightarrow f(a)\) et \(h f (a+ \theta h) \longrightarrow 0\)
d’où \(P(a \leq X \leq a+h) \longrightarrow P(X = a) = 0\)
Remarque : La propriété \(P_2\) implique que \(P(X \leq t) = P(X < t)\).
La fonction de répartition correspond aux probabilités cumulées associées à la variable aléatoire continue sur l’intervalle d’étude (graphe ci-dessous).

L’aire hachurée en vert sous la courbe de la fonction densité de probabilité correspond à la probabilité \(P(X < a)\) et vaut 0,5 car ceci correspond exactement à la moitié de l’aire totale sous la courbe. Cette probabilité correspond à la valeur de la fonction de répartition au point d’inflexion de la courbe (voir cours analyse).
Les propriétés associées à la fonction de répartition sont les suivantes :
Soit \(F_X\) la fonction de répartition d’une variable aléatoire absolument continue \(X\) alors :
(\(P_1\)) \(F_X\) est continue sur \(\mathbb{R}\), dérivable en tout point où \(f\) est continue et alors \(F_X ’ = f\)
(\(P_2\)) \(F_X\) est croissante sur \(\mathbb{R}\)
(\(P_3\)) \(F_X\) est à valeurs dans \([0,1]\)
(\(P_4\)) \(\lim\limits_{t \to - \infty } {F_X (t) = 0}\) et \(\lim\limits_{t \to + \infty } {F_X (t) = 1}\)
Voici pourquoi :
(\(P_1\)) résulte de la relation suivante \(F_X(t) = \int_{- \infty}^{ t } f(x) dx\)
(\(P_2\)) \(F_X' = f\) est donc positive sur \(\mathbb{R}\)
(\(P_3\)) Evident
(\(P_4\)) \(\int_{- \infty}^{ t } f(x) dx\) tend vers 0 quand \(t \longrightarrow { - \infty}\)
Exemple :
Dans une population de canards colverts, lors d’une alerte, l’ensemble des individus quittent leur lieu de repos. Ainsi à \(t = 0\), la surface de l’étang est déserte et la probabilité qu’un canard regagne l’étang entre les temps \(t_1\) et \(t_2\) (en minutes) est donnée par :
\(\int_{t_1}^{t_2} f(t) dt\) avec \(f(t) = 2e^{-t} - 2e^{-2t}\) qui représente la fonction densité de probabilité.
La primitive de \(f(t)\), \({F_T}(t)\), fonction de répartition est de la forme :

L’évolution de la recolonisation de l’étang par les canards colverts en fonction du temps est donnée par la courbe rouge. On observe ainsi que plus de 50 % des canards se posent sur l’étang au cours des 2 premières minutes qui suivent l’alerte. Au bout de 7 minutes, tous les canards ont regagné l’étang. La distribution des probabilités cumulées est donnée sur la courbe verte.
4. Espérance et Variance
Une loi de probabilité peut être caractérisée par certaines valeurs typiques correspondant aux notions de valeur centrale, de dispersion et de forme de distribution.
4.1. Espérance mathématique
L’espérance d’une variable aléatoire \(E(X)\) correspond à la moyenne des valeurs possibles de \(X\) pondérées par les probabilités associées à ces valeurs. C’est un paramètre de position qui correspond au moment d’ordre 1 de la variable aléatoire \(X\). C’est l’équivalent de la moyenne arithmétique \(\bar{X}\). En effet lorsque le nombre d’épreuves \(n\) est grand, \(\bar{X}\) tend vers \(E(X)\) (voir estimation).
4.1.1. Variables aléatoires discrètes
Si \(X\) est une variable aléatoire discrète définie sur un univers probabilisé \(\Omega\), on appelle espérance de \(X\), le réel défini par : \(E(X) = \sum\limits_{\omega \in \Omega } {X(\omega )P(\omega )}\)
Remarque : Si \(X(\Omega)\) est infini, on n’est pas sûr que l’espérance existe. L’espérance mathématique est également notée \(\mu(X)\) ou encore \(\mu_X\) si aucune confusion n’est à craindre.
Nous pouvons donner une autre définition de l’espérance d’une variable aléatoire discrète \(X\)
si à \(\omega \in \Omega\), on associe l’image \(x\) telle que \(X(\omega) = x\).
Théorème :
Si \(X\) est une variable aléatoire discrète de loi de probabilité \((x_i,p_i)_i\) définit sur un nombre fini (\(n\)) d’évènements élémentaires alors :
\(E(X) = \sum\limits_{i=1}^{n} x_i p_i\)
Exemples :
Si l’on reprend l’exemple d’une fratrie de deux enfants, l’espérance de la variable aléatoire « nombre de filles » est :
\(E(X) = 0 \times 1/4 + 1 \times 1/2 + 2 \times 1/4 = 1\) d’où \(E(X) = 1\)
Si l’on observe un nombre suffisant de fratries de 2 enfants, on attend en moyenne une fille par fratrie.
4.1.2. Variables aléatoires continues
Si \(X\) est une variable aléatoire absolument continue de densité \(f\), on appelle espérance de \(X\), le réel \(E(X)\) défini par : \(E(X) = \int_{ - \infty }^{ + \infty } xf(x)dx\)
si cette intégrale est convergente.
Exemple :
Si on reprend l’exemple de la recolonisation de l’étang par les canards colverts, la durée moyenne pour la recolonisation est :
\(E(T) = \int_{0}^{ + \infty } t f(t) dt = \int_{- \infty}^{ + \infty } t (2e^{-t} - 2e^{-2t}) dt =\) \(3/2\) (voir Résultat)
Sous ce modèle, la durée moyenne de recolonisation pour l’ensemble de la population de canards colverts est de 1,5 minutes.
Remarque : Dans cet exemple, la variable étudiée \(t\) ne peut prendre que des valeurs dans \([0, + \infty[\)
4.1.3. Propriétés de l’espérance
Les propriétés de l’espérance valent aussi bien pour une variable aléatoire discrète ou une variable aléatoire absolument continue.
Si \(X\) et \(Y\) sont deux variables aléatoires définies sur un même univers \(\Omega\), admettant une espérance, alors :
(\(P_1\)) \(E(X+Y)=E(X)+E(Y)\)
(\(P_2\)) \(E(aX)=aE(X) \qquad \forall a \in \mathbb{R}\)
(\(P_3\)) Si \(X \geq 0\) alors \(E(X) \geq 0\)
(\(P_4\)) Si \(X\) est un caractère constant tel que : \(\forall ω \in \Omega \qquad\) \(X(\omega) = k\) alors \(E(X) = k\)
Remarque : Dans le cas continu, \(E (X+Y) = \int_{- \infty}^{ + \infty } \int_{- \infty}^{ + \infty } (x+y) f(xy)dxdy\) La propriété \(P_1\) est vérifiée quelques soient les relations de dépendance ou d’indépendance statistique entre les deux variables.
Voici pourquoi :
Nous démontrerons les propriétés dans le cas de deux variables aléatoires discrètes avec \(p_i\), la probabilité de réalisation de \(\{X = x_i\}\) et \(\{Y = y_i\}\) et \(n\) évènements élémentaires.
(\(P_1\)) \(E(X + Y) = \sum\limits_{i = 1}^n {({x_i}} + {y_i}){p_i} = \sum\limits_{i = 1}^n {{x_i}} {p_i} + \sum\limits_{i = 1}^n {{y_i}} {p_i} = E(X) + E(Y)\)
(\(P_2\)) \(E(aX) = \sum\limits_{i = 1}^n {(ax_i)p_i} = a \sum\limits_{i = 1}^n {x_i} {p_i} = aE(X)\)
(\(P_3\)) \(X \geq 0\) implique que \(\forall ω \in \Omega \qquad\) \(X ( ω ) \geq 0\) et comme une probabilité est toujours positive, E(X) 0.
(\(P_4\)) \(E(X) = \sum\limits_{i = 1}^{n} kp_i = k \sum\limits_{i = 1}^{n} p_i = k\) car par définition \(\sum\limits_{i = 1}^{n} p_i = 1\)
Nous verrons les applications directes de ces propriétés dans le cadre des opérations sur les variables aléatoires.
4.2. Variance
La variance d’une variable aléatoire \(V(X)\) est l’espérance mathématique du carré de l’écart à l’espérance mathématique. C’est un paramètre de dispersion qui correspond au moment centré d’ordre 2 de la variable aléatoire \(X\). C’est l’équivalent de la variance observée \(S^2\) . En effet lorsque le nombre d’épreuves \(n\) est grand, \(S^2\) tend vers \(V(X)\) (voir estimation ).
Si \(X\) est une variable aléatoire ayant une espérance \(E(X)\), on appelle variance de \(X\) le réel :
\(V(X) = E([X - E(X)]^2)\)
Autre notation :
\(V(X) = E([X - E(X)]^2 )\)
\(V(X) = E(X^2 – 2XE(X) +E(X)^2 )\)
\(V(X) = E(X^2 ) – 2E[XE(X)] +E[E(X)^2 ] \qquad\) Propriétés \(P_1\) de l’espérance
\(V(X) = E(X^2) – 2E(X)^2 + E(X)^2 = E(X^2) – E(X)^2 \qquad\) Propriétés \(P_4\) de l’espérance\(V(X) = E (X^2 ) – [E(X)]^2\)
Remarque :
Si \(X( \Omega )\) est infini, il n’est nullement évident que \(V(X)\) existe. De plus comme \([X – E(X)]^2 \geq 0\) nécessairement \(V(X) \geq 0\). Par définition, une variance est toujours positive.
La variance est également notée \(\sigma^2\) si aucune confusion n’est à craindre.
Si \(X\) est une variable aléatoire ayant une variance \(V(X)\), on appelle écart-type de \(X\), le réel :
\(\sigma (X) = \sqrt {V(X)}\)
Remarque :
L’écart-type permet de disposer d’un paramètre de dispersion qui s’exprime dans les mêmes unités que la variable aléatoire elle-même.
Le terme « écart-type » se traduit en anglais par le faux-ami « standard deviation ».
4.2.1. Variables aléatoires discrètes
Si \(X\) est une variable aléatoire discrète de loi de probabilité \((x_i,p_i)_i\) définie sur un nombre fini (\(n\)) d’évènements élémentaires alors la variance est égale à :
\(V (X ) = \sum\limits_{i = 1}^{n} (x_i − E (X ))^2 p_i = \sum\limits_{i = 1}^{n} x_i^{2} p_i - E(X)^2\)
Exemple :
Si l’on reprend l’exemple d’une fratrie de deux enfants, la variance de la variable aléatoire « nombre de filles » est :
\(V(X) = 1/4 (O-1)^2 + 1/2 (1-1)^2 + 1/4 (2-1)^2 = 1/2\)
$V(X) = $ 1/2 et \(\sigma (X) =\) 0,7
4.2.2. Variables aléatoires continues
Si \(X\) est une variable aléatoire continue donnée par sa densité de probabilité alors la variance de \(X\) est le nombre réel positif tel que :
\(V(X) = \int_{ - \infty }^{ + \infty } {{{(x - E(X))}^2}f(x)dx = \int_{ - \infty }^{ + \infty } {{x^2}f(x)dx - E{{(X)}^2}}}\)
Exemple :
Dans le cadre de la recolonisation de l’étang par la population de canard colvert, la variance de la loi de probabilité est : \(V(T) = \int_0^{ + \infty } {(t - E(T)} {)^2}f(t)dt\)= 5/4 avec \(\sigma =\) 1,12 (voir Résultat)
4.2.3. Propriétés de la variance
Si \(X\) est une variable aléatoire admettant une variance alors :
(\(P_1\)) \(\forall a \in \mathbb{R}, \quad V (aX) = a^2 V (X)\)
(\(P_2\)) \(\forall (a, b) \in \mathbb{R}, \quad V (aX + b) = a^2 V (X)\)
(\(P_3\)) \(V (X) = 0 \Leftrightarrow X = E(X)\)
Il est possible d’exprimer la variance en fonction du moment d’ordre 1 (\(m_1\)) et du moment d’ordre 2 (\(m_2\)). La variance correspond au moment centré d’ordre 2.
\(V(X) = E([X - E(X)]^2 ) = E(X^2 ) – E(X)^2\)
d’où \(V(X) = E(X^2 ) – E(X)^2 = m_2 - {m_1}^2\)
5. Couples de variables aléatoires
5.1. Loi jointe
Les définitions portant sur la loi jointe entre deux variables aléatoires \(X\) et \(Y\) impliquent que ces dernières soient définies sur le même espace fondamental \(\Omega\). Si \(X\) et \(Y\) sont définies respectivement sur les espaces fondamentaux \(\Omega_1\) et \(\Omega_2\), alors il faut envisager un espace qui englobe \(\Omega_1\) et \(\Omega_2\) appelé « espace-produit ».
Il suffit alors de connaître la loi jointe des deux variables aléatoires ou loi de probabilité du couple \((X,Y)\),la fonction définie par :
\(x,y \longrightarrow p_{xy} = P ((X = x) \ \text{et} \ (Y = y))\) dans le cas discret.
Dans le cas continu, \(p_{xy} = P ((x a < X < x b ) \ \text{et} \ (y c < Y < y d ))\) permet de définir la probabilité pour que \((X,Y)\) soit dans un rectangle.
Remarque : Ceci peut être généralisé à un nombre quelconque de variables aléatoires.
Exemple :
On place au hasard deux billes rouge et verte dans deux boites A et B. On note \(X\), la variable aléatoire « nombre de billes dans la boite A » et \(Y\), la variable aléatoire « nombre de boites vides ».

Les distributions de probabilités associées à chacune des variables \(X\) et \(Y\) ainsi que celle de la loi jointe sont indiquées ci-dessous. Pour chaque loi, la valeur de l’espérance et de la variance est également indiquée.

5.2. Indépendance entre variables aléatoires
Les propriétés concernant l’indépendance statistique entre deux variables aléatoires s’appliquent aussi bien aux variables aléatoires discrètes ou absolument continues.
Théorème :
Si \(X\) et \(Y\) sont deux variables aléatoires indépendantes définies sur le même univers \(\Omega\)
alors: \(E(XY) = E(X)E(Y)\)
Remarque : L’application réciproque n’est pas vraie. La relation \(E(XY) = E(X)E(Y)\) n’implique pas forcément l’indépendance de deux variables aléatoires.
Exemple :
Dans l’exemple concernant la répartition des deux billes dans les 2 boites, la relation E(XY) = E(X)E(Y) est vérifiée car : \(E(X) = 1\) ; \(E(Y) = 1/2\) et \(E(XY) = 1/2\)
cependant les variables aléatoires \(X\) et \(Y\) ne sont pas indépendantes.
En effet \({\rho_{00}} = P ((X = 0) \cap (Y = 0)) = 0\) car il est impossible d’avoir à la fois aucune bille dans la boite A et aucune boite vide. Or on attend si \(X\) et \(Y\) sont deux variables statistiquement indépendantes, à ce que
\(P ((X = 0) \cap (Y = 0)) = P(X = 0)P(Y = 0) = 1/4 \times 1/2 =\) \(1/8 \neq 0\)
Théorème :
Si \(X\) et \(Y\) sont deux variables aléatoires indépendantes définies sur le même univers \(\Omega\) alors \(V(X + Y) = V(X) + V(Y)\) Démonstration
Remarque :
L’application réciproque n’est pas vraie. La relation \(V(X + Y) = V(X) + V(Y)\) n’implique pas forcément l’indépendance de deux variables.
Exemple :
Si l’on reprend l’exemple de la répartition de deux billes dans deux boites, la distribution de probabilité de la variable aléatoire \((X+Y)\) est :

Comme \(V(X) = 1/2\) et \(V(Y) = 1/4\) alors \(V(X) + V(Y) = 3/4 = V(X+Y)\)
On retrouve ainsi la relation \(V(X + Y) = V(X) + V(Y)\) bien que \(X\) et \(Y\) ne soient pas indépendantes (?theme=proba&chap=3#X et Y ne sont pas )).
5.3. Covariance et Corrélation
Lorsque l’on considère deux variables aléatoires simultanément, il faut définir un indicateur de leur « liaison » qui complète les paramètres qui les caractérisent chacune séparément (espérance mathématique et variance).
Si \(X\) et \(Y\) sont deux variables aléatoires définies sur le même univers \(\Omega\), on appelle covariance de ces deux variables, le réel :
\(\text{cov}(X,Y) = E(XY) - E(X)E(Y)\)
et coefficient de corrélation, le réel :
\(R(X, Y) = \frac{\text{cov}(X,Y)}{\sigma (X) \sigma (Y)}\)
Il résulte de cette définition, le théorème suivant :
Théorème :
Si \(X\) et \(Y\) sont deux variables aléatoires définies sur le même univers \(\Omega\) et indépendantes, alors : \(\text{cov}(X,Y) = 0\)
Les propriétés de la covariance sont les suivantes :
Si \(X\) et \(Y\) sont deux variables aléatoires définies sur un même univers \(\Omega\), alors :
(\(P_1\)) \(\forall (a,b) \in \mathbb{R} \qquad V(aX + bY) = a^2 V(X) + 2ab \times \text{cov} (X,Y) + b^2 V(Y)\)
(\(P_2\)) \([\text{cov}(X,Y)]^2 \leq V(X) V(Y)\)
\(| \text{cov}(X,Y) | \leq \sigma (X) \sigma (Y)\)
(\(P_3\)) \(-1 \leq R(X,Y) \leq 1\)
Remarque :
Si \(X\) et \(Y\) sont indépendantes, \(\rho=0\) mais la réciproque est fausse. Il peut arriver, par hasard, que \(\rho=0\) sans que \(X\) et \(Y\) soient indépendantes.
5.4. Opérations sur les variables aléatoires
Il arrive souvent que l’on effectue des transformations sur les variables aléatoires par commodité de calcul et il est important de savoir comment se comportent les paramètres associés à cette variable.
Nous avons résumé dans le tableau ci-dessous quelques transformations possibles avec \(a \ \text{et} \ b \in \mathbb{R}\).

Il existe d’autres transformations de variables aléatoires qui conduisent à des valeurs de paramètres particulières.
Une variable aléatoire \(X\) est dite centrée si \(E(X) = 0\).
Exemple :
La variable \(Y = X – E(X)\) est une variable aléatoire centrée car
\(E(Y) = E[X – E(X)] = E(X ) – E(E(X))\)
or \(E(E(X)) = E(X )\) voir propriétés \(P_4\) de l’espérance
ainsi \(E(Y) = E(X ) – E(X) = 0\)
Une variable aléatoire admettant une variance est dite réduite si \(V(X) = 1\).
Exemple :
La variable \(Y = \frac{ X } { \sqrt{V(X)} }\) est une variable aléatoire réduite car
\(V(Y) = E({Y^2}) - E{(Y)^2} = E\left[ {{{\left( {\frac{X}{{\sqrt {V(X)} }}} \right)}^2}} \right] - {\left[ {E\left( {\frac{X}{{\sqrt {V(X)} }}} \right)} \right]^2}\)
\(V(Y) = \frac{1}{{V(X)}}E({X^2}) - {\left[ {\frac{1}{{\sqrt {V(X)} }}E(X)} \right]^2}\) voir propriétés \(P_2\) de l’espérance
\(V(Y) = \frac{1}{{V(X)}}[E({X^2}) - E{(X)^2}]\) d’où \(V(Y) = \frac{{V(X)}}{{V(X)}} = 1\)
A toute variable aléatoire \(X\) d’espérance \(E(X)\) et de variance \(V(X)\) on peut associer la variable aléatoire \(\frac{{X - E(X)}}{{\sqrt {V(X)} }}\) dite variable aléatoire centrée réduite et dont l’emploi est indispensable pour utiliser la plupart des tables notamment les tables de la loi normale réduite.
5.5. Généralisation à n variables aléatoires
Si l’on considère une épreuve à laquelle est associée un espace fondamental \(\Omega\) et une variable aléatoire \(X\) et si l’on répète \(n\) fois, de façon indépendante cette épreuve, on obtient une suite \(X_1 , X_2 ,....... X_n\) variables aléatoires qui sont :
définies sur le même espace fondamental
de même loi de probabilité
indépendantes
alors :
\(E(X_1 + X_2 +...+ X_i +. ...X_n ) = \sum\limits_{i=1}^{n} E(X_i) \qquad\) (?theme=proba&chap=3#propriétés de l’espérance) que les v.a. soient indépendantes ou non )
\(V(X_1 + X_2 +...+ X_i +. ...X_n ) = \sum\limits_{i=1}^{n} V(X_i) \qquad\) (?theme=proba&chap=3#indépendance) des v.a.)