Chapitre 3 — Dérivation – Etude de fonctions

Vers d’autres sites…

15873: un site dédié aux mathématiques utilitaires de tous niveaux, sous forme d’exercices avec leurs solutions. Avec une partie “Aide Mémoire” (formulaire) pour les choses courantes.

Voir le formulaire des dérivées

1.1 Dérivée en un point – Dérivée sur un intervalle

Définition 1 :

Soient \(f:I \to \mathbb{R}\) et \({x_0} \in I\). On dit que \(f\) est dérivable au point \({x_0}\) si et seulement si la quantité \(\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) admet une limite finie lorsque \(x\) tend vers \({x_0}\).

On note alors \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) ;

\(f'\left( {{x_0}} \right)\) est appelé nombre dérivé ou dérivée de \(f\) en \({x_0}\).

Autres notations : \(D\left( f \right)\left( {{x_0}} \right)\) ou \(\frac{{df}}{{dx}}\left( {{x_0}} \right)\)

Remarque :

Une définition équivalente à la précédente s’obtient en posant \(x = {x_0} + h\) :

\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {{x_0} + h} \right) - f\left( {{x_0}} \right)}}{h}\)

Définition 2 :

Soit \(f:I \to \mathbb{R}\). On dit que \(f\) est dérivable sur \(I\) si elle est dérivable en tout point de \(I\).

Exemple 1

1.2 Dérivées à gauche et à droite

Définition 3 :

Soient \(f:I \to \mathbb{R}\) et \({x_0} \in I\). On dit que \(f\) est dérivable à droite (resp. à gauche) au point \({x_0}\) si et seulement si la quantité \(\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) admet une limite finie lorsque \(x\) tend vers \({x_0}\) par valeurs supérieures (resp. inférieures) :

\({f'_d}\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to x_0^ + } \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) : dérivée à droite de \(f\) en \({x_0}\), notée aussi \({f'_ + }\left( {{x_0}} \right)\).

\({f'_g}\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to x_0^ - } \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) : dérivée à gauche de \(f\) en \({x_0}\), notée aussi \({f'_ - }\left( {{x_0}} \right)\).

Proposition :

Soient \(f:I \to \mathbb{R}\) et \({x_0} \in I\). \(f\) est dérivable au point \({x_0}\) si et seulement si \(f\) est dérivable à droite et à gauche en \({x_0}\), et \({f'_d}\left( {{x_0}} \right) = {f'_g}\left( {{x_0}} \right)\).

Cette proposition découle directement de la définition des limites à droite et à gauche.

Exemples 2

1.3 Fonctions dérivées

Définition 4 :

Soit \(f\) une fonction dérivable sur \(I\). La fonction dérivée ou dérivée de \(f\) sur \(I\) est la fonction \(f'\) qui a tout \(x\) de \(I\) associe \(f'\left( x \right)\).

Remarque :

L’ensemble de définition de \(f'\) est le sous-ensemble de \(I\) sur lequel \(f\) est dérivable : \({D_{f'}} \subseteq I\).

Exemple 3

1.4 Développement limité d’ordre 1

Définition :

Une fonction \(f\) admet un développement limité d’ordre 1 en \({x_0}\) s’il existe \(\alpha \in \mathbb{R}\) et une fonction $$ définie sur un voisinage \(V\) de \({x_0}\) tels que :

\(\forall x \in V\), \(f\left( * \right) = f\left( {{x_0}} \right) + \left( {x - {x_0}} \right)\alpha + \left( {x - {x_0}} \right)\varepsilon \left( x \right)\) avec \(\mathop {\lim }\limits_{x \to {x_0}} \varepsilon \left( x \right) = 0\) et \(\varepsilon \left( {{x_0}} \right) = 0\)

Proposition :

\(f\) est dérivable en \({x_0}\) si et seulement si \(f\) admet un développement limité d’ordre 1 en \({x_0}\). On a alors :

\(f\left( x \right) = f\left( {{x_0}} \right) + \left( {x - {x_0}} \right)f'\left( {{x_0}} \right) + \left( {x - {x_0}} \right)\varepsilon \left( x \right)\) avec \(\mathop {\lim }\limits_{x \to {x_0}} \varepsilon \left( x \right) = 0\) et \(\varepsilon \left( {{x_0}} \right) = 0\).

Démonstration

Remarque :

\[P\left( x \right) = \underbrace {f\left( {{x_0}} \right) - {x_0}f'\left( {{x_0}} \right)}_{{\text{Une constante}}} + \underbrace {f'\left( {{x_0}} \right)x}_{{\text{terme du }}{{\text{1}}^{{\text{er}}}}{\text{ degré en }}x}\]

du moins tant que \(x\) est voisin de \({x_0}\).

Exemple :

Considérons la fonction définie par \(f\left( * \right) = a{x^2}\). On calcule aisément \(f'\left( * \right) = 2ax\).

Il vient d’après la proposition précédente : \(f\left( x \right) = f\left( {{x_0}} \right) + \left( {x - {x_0}} \right)f'\left( {{x_0}} \right) + \left( {x - {x_0}} \right)\varepsilon \left( x \right) \Leftrightarrow a{x^2} * ax_0^2 + 2ax\left( {x - {x_0}} \right) + \left( {x - {x_0}} \right)\varepsilon \left( x \right)\)

1.5 Lien entre dérivabilité et continuité

Théorème :

Soit \(f:I \to \mathbb{R}\). Si \(f\) est dérivable en \({x_0}\), alors \(f\) est continue en \({x_0}\).

Démonstration

!* Attention* : La réciproque est fausse, c’est-à-dire que la continuité n’implique pas nécessairement la dérivabilité.

Exemples :

• La fonction définie sur \(\mathbb{R}\) par \(f\left( x \right) = \left| x \right|\) est continue en 0 mais non dérivable en 0.

• Considérons la fonction suivante :

  \(\left\{ \begin{gathered} f\left( x \right) = x\sin \frac{1}{x}{\text{, si }}x \ne 0 \hfill \\* f\left( 0 \right) = 0 \hfill \\\end{gathered} \right.\)

  La question de la continuité et de la dérivabilité se pose en 0. Réponse.

2.1 Tangentes

Définitions :

Soit \(f:I \to \mathbb{R}\) dérivable en \({x_0}\). Alors \(f\) admet un développement limité d’ordre 1 en \({x_0}\) :

\(f\left( x \right) = f\left( {{x_0}} \right) + \left( {x - {x_0}} \right)f'\left( {{x_0}} \right) + \left( {x - {x_0}} \right)\varepsilon \left( x \right)\) avec \(\mathop {\lim }\limits_{x \to {x_0}} \varepsilon \left( x \right) = 0\) et \(\varepsilon \left( {{x_0}} \right) = 0\)

1. \(f\left( {{x_0}} \right) + \left( {x - {x_0}} \right)f'\left( {{x_0}} \right)\) est l’approximation polynomiale de degré 1 de \(f\) en \({x_0}\).

2. L’équation \(y = f\left( {{x_0}} \right) + \left( {x - {x_0}} \right)f'\left( {{x_0}} \right)\) est l’équation de la tangente désignée par T à la courbe représentative de \(f\), au point \({x_0}\).

Le nombre dérivé \(f'\left( {{x_0}} \right)\) est le coefficient directeur (ou pente) de la tangente.

Exemple 4

Propriétés :

Soit \(f:I \to \mathbb{R}\) dérivable en \({x_0}\). Soit \(\left( \Gamma \right)\) courbe représentative de \(f\).

\(f'\left( {{x_0}} \right)\) est donc la pente de la tangente T à \(\left( \Gamma \right)\) au point \({x_0}\).

1. Si \(f'\left( {{x_0}} \right) = 0\), alors T est une droite parallèle à l’axe des \(x\) ;

2. Si $_{x } f’( x ) = $, alors T est une droite parallèle à l’axe des \(y\).

Exemple 5

2.2 Interprétation géométrique

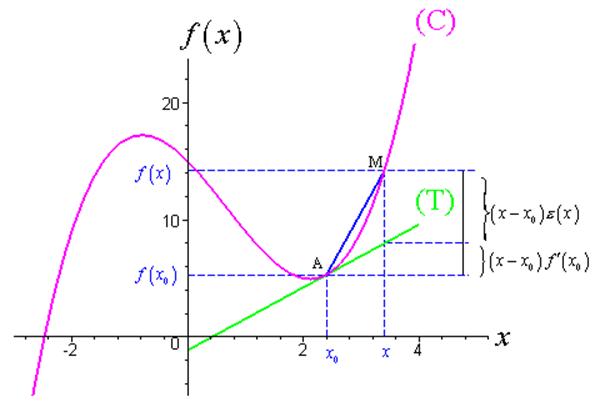
Soit \({\text{A}}\left( {{x_0},f\left( {{x_0}} \right)} \right)\) et \({\text{M}}\left( {x,f\left( x \right)} \right)\) sur la courbe représentative (C) de la fonction \(f\).

Le taux d’accroissement \(\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) correspond au coefficient directeur de la corde AM.

Dire que \(f\) est dérivable en \({x_0}\) revient à dire que la corde AM possède une position limite non verticale (T) de coefficient directeur \(f'\left( x \right)\) quand \(x\) tend vers \({x_0}\), c’est-à-dire quand M tend vers A.

20. est la tangente à (C) au point d’abscisse \({x_0}\).

Unnamed Image

Ce qui précède est inspiré du chapitre 8 « Dérivation, connexité», une aide à l’interprétation géométrique de la notion de dérivée et de tangente à une courbe sur le site M@ths En Prép@.

4.1 Opérations élémentaires

4.2 Fonction inverse et quotient de fonctions dérivables

Proposition *:

Soit \(g\) une fonction définie sur \(I \subseteq \mathbb{R}\) et dérivable en \({x_0}\).

Si \(g\left( {{x_0}} \right) \ne 0\), alors la fonction \(h = \frac{1}{g}\) est dérivable en \({x_0}\) et \(h'\left( {{x_0}} \right) = - \frac{{g'\left( {{x_0}} \right)}}{{{g^2}\left( {{x_0}} \right)}}\).

Par extension, si \(g\) ne s’annule pas sur \(I\), alors la fonction \(h = \frac{1}{g}\) est dérivable sur \(I\) avec

\(h' = - \frac{{g'}}{{{g^2}}}\).

Exemple :

Soit la fonction définie sur \({\mathbb{R}^{ * * }}\backslash \left\{ 1 \right\}\) par \(g\left( * \right) = \frac{1}{{\ln x}}\). \(g\) ne s’annule pas sur \({\mathbb{R}^{ * * }}\backslash \left\{ 1 \right\}\).

\({\left( {\ln x} \right)^\prime } = \frac{1}{x}\) Il vient \(g'\left( x \right) = - \frac{1}{{x{{\ln }^2}x}}\). Graphe.

Proposition *:

Soient \(f\) et \(g\) deux fonctions définies sur \(I \subseteq \mathbb{R}\) et dérivables en \({x_0}\).

Si \(g\left( {{x_0}} \right) \ne 0\), alors la fonction \(h = \frac{f}{g}\) est dérivable en \({x_0}\) et

\(h'\left( {{x_0}} \right) = \frac{{f'\left( {{x_0}} \right)g\left( {{x_0}} \right) - f\left( {{x_0}} \right)g'\left( {{x_0}} \right)}}{{{g^2}\left( {{x_0}} \right)}}\).

Par extension, si g ne s’annule pas sur \(I\), alors la fonction \(h = \frac{f}{g}\) est dérivable sur \(I\) avec

\(h' = \frac{{f'g - fg'}}{{{g^2}}}\).

Exemple 6

4.3 Composition

Proposition *:

Soient \(f:I \to \mathbb{R}\) et \(g:J \to \mathbb{R}\) deux fonctions telles que \(f\left( I \right) \subseteq J\).

Si \(f\) est dérivable en \({x_0}\) et si \(g\) est dérivable en \({y_0} * f\left( {{x_0}} \right)\), alors \(g \circ f\) est dérivable en \({x_0}\) et \({\left( {g \circ f} \right)^\prime }\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {g' \circ f} \right)\left( {{x_0}} \right)\).

Par extension, si \(f\) est dérivable sur \(I\) et \(g\) dérivable sur \(J\), alors \(g \circ f\) est dérivable est dérivable sur \(I\) et \({\left( {g \circ f} \right)^\prime } = f'.\left( {g' \circ f} \right)\).

Exemple 7

4.4 Fonction réciproque

Proposition *:

Soit \(f:I \to J\) une fonction strictement monotone et dérivable en \({x_0}\) tel que \(f'\left( {{x_0}} \right) \ne 0\).

\(f\) est donc bijective de \(I\) sur \(J\), et admet une fonction réciproque \({f^{ * 1}}:J \to I\).

Alors \({f^{ * 1}}\) est dérivable en \({y_0} = f\left( {{x_0}} \right)\) et \({\left( {{f^{ - 1}}} \right)^\prime }\left( {{y_0}} \right) = \frac{1}{{f'\left( {{x_0}} \right)}} = \frac{1}{{\left( {f' \circ {f^{ - 1}}} \right)\left( {{y_0}} \right)}}\).

Par extension, si \(f'\) ne s’annule pas sur \(I\), alors \({f^{ * 1}}\) est dérivable sur \(J\) et \({\left( {{f^{ - 1}}} \right)^\prime } = \frac{1}{{f' \circ {f^{ - 1}}}}\).

Exemple 8

4.5 Dérivées successives

6.1 Théorème

Théorème des accroissements finis (Généralisation du théorème de Rolle) :

Soit \(f\) une fonction vérifiant les conditions suivantes :

• \(f\) est définie et continue sur un intervalle fermé \(\left[ {a,b} \right]\),

• \(f\) est dérivable sur \(\left] {a,b} \right[\),

Alors il existe au moins une valeur \(c\) de l’intervalle ouvert \(\left] {a,b} \right[\) telle que :

\(f\left( b \right) - f\left( a \right) = \left( {b - a} \right)f'\left( c \right) \Leftrightarrow f'\left( c \right) = \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\)

! Attention ! Comme pour le théorème de Rolle, il n’y a pas nécessairement unicité de \(c\).

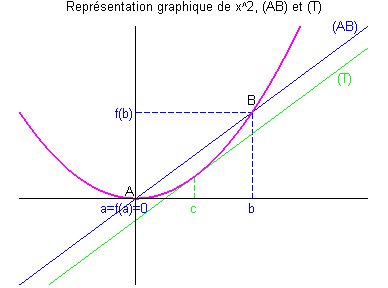
Interprétation géométrique :

Soient A et B les points de coordonnées respectives \(\left( {a,f\left( a \right)} \right)\) et \(\left( {b,f\left( b \right)} \right)\).

\(\frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}\) est le coefficient directeur de la droite (AB).

\(f'\left( c \right)\) est le coefficient directeur de la tangente T à la courbe représentative de \(f\) au point \(c\).

• Le théorème des accroissements finis permet de dire qu’il existe au moins un point \(c\) de \(\left] {a,b} \right[\) où la tangente T est parallèle à (AB).

Unnamed Image

Démonstration

Exemple d’utilisation

Soient \(f\) et \(g\) deux fonction définies pour \(x > 0\) par :

\(f\left( x \right) = \ln \left( {1 + x} \right) - \ln x - \frac{1}{{1 + x}}\) et \(g\left( x \right) = \ln \left( {1 + x} \right) - \ln x - \frac{1}{x}\)

Montrons que \(g\left( x \right) < 0 < f\left( x \right)\). Réponse.

6.2 Théorème des accroissements finis généralisés

Théorème :

Soient \(f\) et \(g\) deux fonctions vérifiant les conditions suivantes :

• \(f\) et \(g\) sont définies et continues sur \(\left[ {a,b} \right]\),

• \(f\) et \(g\) sont dérivables sur \(\left] {a,b} \right[\),

• \(g'\left( * \right)\) ne s’annule pas sur \(\left] {a,b} \right[\),

Alors il existe au moins une valeur \(c\) de l’intervalle ouvert \(\left] {a,b} \right[\) telle que :

\(\frac{{f\left( b \right) - f\left( * \right)}}{{g\left( b \right) - g\left( a \right)}} = \frac{{f'\left( c \right)}}{{g'\left( c \right)}}\)

! Attention ! Il n’y a pas nécessairement unicité du point \(c\).

Démonstration

6.3 Règle de L’Hospital

6.4 Théorème du point fixe

Théorème :

Soit \(f\) une fonction continue de \(\left[ {a,b} \right]\) dans \(\left[ {a,b} \right]\), alors \(\exists * \in \left[ {a,b} \right]\) tel que \(f\left( * \right) = c\).

Si de plus \(f\) est dérivable sur \(\left[ {a,b} \right]\) et que \(\forall x \in \left[ {a,b} \right]\) \(\left| {f'\left( x \right)} \right| \leqslant k < 1\), alors \(c\) est unique.

Exemple 17

7.1 Définitions

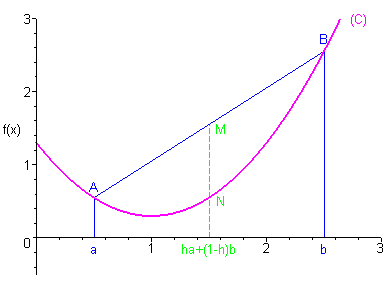
Une fonction est dite convexe si son graphe à la forme suivante : courbe (C). *

Les coordonnées des différents points de la courbe sont :

\(A\left( {a,f\left( a \right)} \right)\)

\(B\left( {b,f\left( b \right)} \right)\)

\(N\left( {{x_h},f\left( {{x_h}} \right)} \right)\)

\(M\left( {{x_h},hf\left( a \right) + \left( {1 - h} \right)f\left( b \right)} \right)\)

avec \({x_h} = ha + \left( {1 - h} \right)b\)

Unnamed Image

La convexité de \(f\) signifie que pour tout \(h \in \left[ {0;1} \right]\), l’ordonnée de N est inférieure ou égale à celle de M.

Lorsque \(h\) décrit \(\left[ {0;1} \right]\), * parcourt l’arc \(\left( {{\text{AB}}} \right)\), tandis que M parcourt la corde \(\left[ {{\text{AB}}} \right]\).

Ainsi, dire que \(f\) est convexe signifie que pour tous les points de la courbe entre A et B, la corde \(\left[ {{\text{AB}}} \right]\) est « au-dessus » de l’arc \(\left( {{\text{AB}}} \right)\).

Définition :

\(f:I \to \mathbb{R}\) est dite convexe sur \(I\) si et seulement si :

\(\forall h \in \left[ {0;1} \right]\), \(\forall \left( {a,b} \right) \in {I^2}\), \(f\left( {ha + \left( {1 - h} \right)b} \right) \leqslant hf\left( a \right) + \left( {1 - h} \right)f\left( b \right)\)

Exemples 18

Propositions 1 :

1. \(\forall \left( {a,b,c} \right) \in {I^2}\) tels que \(a < b < c\), \(\frac{{f\left( b \right) - f\left( a \right)}}{{b - a}} \leqslant \frac{{f\left( c \right) - f\left( a \right)}}{{c - a}} \leqslant \frac{{f\left( c \right) - f\left( b \right)}}{{c - b}}\) * (Inégalité des trois points)

2. \(\forall a \in I\), \({T_a}:I\backslash \left\{ a \right\} \to \mathbb{R}\) définie par \({T_a}\left( x \right) = \frac{{f\left( x \right) - f\left( a \right)}}{{x - a}}\) est croissante.

Ces propositions sont équivalentes à la définition.

Définition 2 :

\(f:I \to \mathbb{R}\) est dite concave si \(\left( { - f} \right)\) est convexe.

Exemple :

La fonction définie sur \(\mathbb{R}\) par \(f\left( * \right) = - {x^2}\) est concave. Voir graphe précédent.

Proposition 2 :

Les fonctions affines définies sur \(\mathbb{R}\) par $f( * ) = x + $, dont la courbe représentative est une droite, sont à la fois convexes et concaves sur \(\mathbb{R}\).

Démonstration

Proposition 3 :

Soient \({f_1}\), \({f_2}\), …, \({f_n}\) des fonctions définies de \(I\) dans \(\mathbb{R}\), et convexes sur \(I\). Alors \(\forall {\alpha _1},{\alpha _2}, \ldots ,{\alpha _n} \in \mathbb{R}\), la fonction \(g = {\alpha _1}{f_1} + {\alpha _2}{f_2} + \ldots + {\alpha _n}{f_n}\) définie de \(I\) dans \(\mathbb{R}\), est aussi convexe.

7.2 Critères de convexités

Proposition 4 (caractérisation de la convexité par la dérivée première) :

Soit \(f:I \to \mathbb{R}\) dérivable. Alors \(f\) est convexe si et seulement si \(f'\) est croissante sur \(I\).

Conséquence (tangente à la courbe d’une fonction convexe) :

Soit \(f:I \to \mathbb{R}\) dérivable et convexe. Alors pour tout \({x_0} \in I\), on a : * \(\forall x \in I\), \(f\left( x \right) \geqslant f\left( {{x_0}} \right) + \left( {x - {x_0}} \right)f'\left( {{x_0}} \right)\)

Autrement dit, la courbe représentative de \(f\) est partout au-dessus des tangentes.

Exemple 19

Proposition 5 (caractérisation de la convexité par la dérivée seconde) :

Soit \(f:I \to \mathbb{R}\) deux fois dérivable. Alors \(f\) est convexe si et seulement \(f''\left( x \right) \geqslant 0\) \(\forall * \in I\).

Exemple :

Considérons à nouveau la fonction définie sur \(\mathbb{R}\) par \(f\left( x \right) = {x^2}\).

\(f''\left( x \right) = 2 \geqslant 0\) sur \(\mathbb{R}\) tout entier.

Définition 3 :

Soient \(f:I \to \mathbb{R}\) deux fois dérivable et \({x_0} \in I\), différent des bornes. On dit que \({x_0}\) est un point d’inflexion si \(f''\) s’annule et change de signe au point \({x_0}\) ;

On dit que la courbe représentative de \(f\) « traverse » la tangente au point \({x_0}\).

Exemple 20

8.1 Dérivation et extremums d’une fonction

Proposition :

Soit \(f:I \to \mathbb{R}\) une fonction dérivable sur \(I\). Soit \({x_0} \in I\), et différent des bornes.

Si \(f\) possède un extremum local en \({x_0}\), alors \(f'\left( {{x_0}} \right) = 0\).

Remarque :

Le terme d’extremum local s’emploie lorsque la notion d’extremum n’est valable que dans un intervalle \(J \subset I\).

Exemples 21

! Attention ! La réciproque de la proposition précédente est fausse.

Contre-Exemple

8.2 Etude d’une fonction

8.3 Résolution de l’équation $f( x ) = $

Ce paragraphe est traité d’un point de vue pratique en s’inspirant de l’ouvrage de Misset et al (p134).

9.1 En Biologie

L’exemple présenté ci-après est tiré d’un TP de biochimie d’une classe de Terminale option Biologie-Génie Biochimique ; ce TP et bien d’autres sont disponibles à l’adresse suivante : http://wwwusers.imaginet.fr/~dhirou/tp.html.

L’activité d’une enzyme (par exemple la b-galactosidase) est fortement influencée par le pH du milieu réactionnel (d’où l’utilisation de milieux tamponnés pour mesurer des activités catalytiques). C’est au pH optimum que l’activité est la plus grande, aux pH d’arrêt l’activité est nulle. Les variations de pH peuvent modifier la conformation de la protéine soit en la dénaturant (pH extrêmes) soit en induisant des changements réversibles (faibles variations autour du pH optimum).

De même, l’activité enzymatique dépend de la température, la température critique correspond à la limite à partir de laquelle l’activité baisse, suite à la dénaturation de l’enzyme.

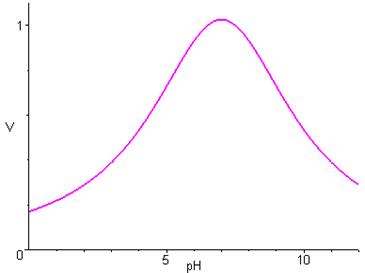
On note \(V\) la vitesse d’une réaction catalysée par la b-galactosidase, exprimée en unités enzymatique. On admet alors la relation suivante :

\({\text{V}} = \frac{1}{{1 + 0.1\left( {{\text{pH}} - 7.5} \right) + 0.1{{\left( {{\text{pH}} - 7.5} \right)}^2}}}\)

La représentation graphique de cette relation V – pH est la suivante :

Unnamed Image

On constate qu’il existe une vitesse maximale pour une certaine valeur du pH.

Posons \(g\left( x \right) = 1 + 0.1\left( {x - 7.5} \right) + 0.1{\left( {x - 7.5} \right)^2}\) et \(f\left( x \right) = \frac{1}{{g\left( x \right)}}\). Alors \({\text{V}} = f\left( {{\text{pH}}} \right)\).

On obtient pour la dérivée (cf. § 4.2.) :

\(f'\left( x \right) = - \frac{{g'\left( x \right)}}{{{g^2}\left( x \right)}} = - \frac{{0.1 + 0.2\left( {x - 7.5} \right)}}{{{{\left[ {1 + 0.1\left( {x - 7.5} \right) + 0.1{{\left( {x - 7.5} \right)}^2}} \right]}^2}}} = \frac{{1.4 - 0.2x}}{{{{\left[ {1 + 0.1\left( {x - 7.5} \right) + 0.1{{\left( {x - 7.5} \right)}^2}} \right]}^2}}}\)

Ainsi \(f'\left( x \right) = 0 \Leftrightarrow x = 7\). Par conséquent le pH optimum est égal à 7.

9.2 En Physique

L’exemple ci-après est extrait de Misset et al. (p138).

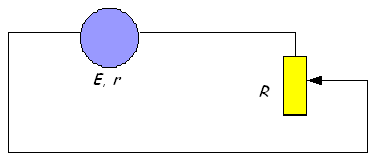
On considère un générateur de force électromotrice \(E\) et de résistance interne \(r\) qui débite sur un résistor de résistance R variable. On note \(P\) la puissance dépensée dans le résistor et \(i\) l’intensité du courant.

On a les relations suivantes :

\(E = \left( {r + R} \right)i\) et \(P = R{i^2}\)

Les unités sont les suivantes :

E en volts (V)

\(R,r\) en ohms \(\left( \Omega \right)\)

P en watts (W)

\(i\) en ampère (A)

Unnamed Image

En supposant \(E = 3\,{\text{V}}\) et $r = 0.5,$, on peut exprimer \(P\) comme une fonction de \(R\) :

\(P = f\left( R \right)\) avec \(f\left( * \right) = \frac{{9R}}{{{{\left( {R + 0.5} \right)}^2}}}\)

Voici la représentation graphique de la fonction \(f\) :

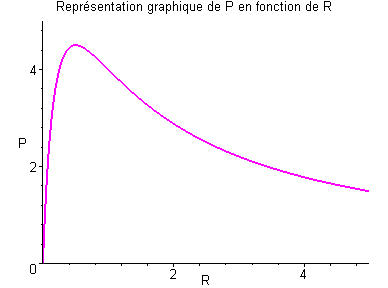
Unnamed Image

On constate que la puissance est maximale pour une certaine valeur de R.

Recherchons cette valeur \({R_0}\) telle que \(f\left( {{R_0}} \right) = {P_{\max }}\).

\(f'\left( R \right) = \frac{{ - 9R + 4.5}}{{{{\left( {R + 0.5} \right)}^3}}}\)

\(f'\left( R \right) = 0 \Leftrightarrow {R_0} = 0.5\)

La résistance à laquelle la puissance dépensée dans le résistor est maximale est égale à ${R_0} = 0.5,$. La puissance alors dépensée vaut à \({P_{\max }} = 4.5\,{\text{W}}\).