Chapitre 2 — Applications linéaires
Sandrine CHARLES : scharles@biomserv.univ-lyon1.fr
Introduction
Les applications linéaires constituent un chapitre considérable des mathématiques modernes, tant par sa densité au-delà de son développement propre : calcul matriciel ; théorie des déterminants ; formes quadratiques ; espaces fonctionnels… ; que par l’importance de son emploi dans les autres sciences : Recherche opérationnelle ; Sciences économiques ; Mécanique quantique ; Théorie de la relativité ; Biologie (dynamique des populations)… Ceci est dû, en particulier, aux nombreuses interventions des systèmes d’équations algébriques, différentielles ou aux dérivées partielles, dont la résolution utilise les applications linéaires et le calcul matriciel qui leur est lié (voir chapitre 3). Source : http://www.chronomath.com/.
Considérons deux ensembles non vides quelconque \(E\) et \(F\). Supposons qu’à chaque élément de \(E\) on fasse correspondre un unique élément de \(F\). L’ensemble de ces correspondances est appelé une application de \(E\) vers F ; on la note \[f:E \to F\]. On note également \[f\left( a \right)\] l’élément de \(F\) associé à \[a \in E\].
Dans le cours d’analyse nous avions également parlé d’applications (que nous avions désigné sous le terme fonctions) mais de \[\mathbb{R}\] dans \[\mathbb{R}\], c’est-à-dire des applications réelles d’une variable réelle.
Supposons que les deux ensembles non vides quelconques \(E\) et \(F\) sont munis chacun d’une loi de composition interne: \[\left( {E, \wedge } \right)\] et \[\left( {F, \vee } \right)\]. On dit que \[f:E \to F\] est un morphisme (on dit encore homomorphisme) lorsque :
\[\forall \left( {a,b} \right) \in E\], \[f\left( {a \wedge b} \right) = f\left( a \right) \vee f\left( b \right)\]
On désigne alors par endomorphisme de \[\left( {E, \wedge } \right)\] un morphisme de \[\left( {E, \wedge } \right)\] dans lui-même ; par isomorphisme un morphisme bijectif ; et par automorphisme un endomorphisme bijectif.
Les applications linéaires sont des morphismes d’espace vectoriel, c’est-à-dire des applications d’un espace vectoriel dans un autre espace vectoriel. C’est tout l’objet de ce chapitre 2.
1 Généralités
Définition
Soient* E* et* F* deux espaces vectoriels sur \[\mathbb{R}\] et \(f\) une application de* E* dans* F*. On dit que \(f\) est une application linéaire si et seulement si l’image d’une combinaison linéaire est la combinaison linéaire des images.
Autrement dit :
\[\forall \vec x,\vec y \in E\] et \[\forall \lambda ,\mu \in \mathbb{R}\], \[f\left( {\lambda \vec x + \mu \vec y} \right) * \lambda f\left( {\vec x} \right) + \mu f\left( {\vec y} \right)\]
Et plus généralement :
\[\forall {\vec x_1}, \ldots ,{\vec x_n} \in E\], \[\forall {\lambda _1}, \ldots ,{\lambda _n} \in \mathbb{R}\], \[f\left( {{\lambda _1}{{\vec x}_1} + \ldots + {\lambda _n}{{\vec x}_n}} \right) = {\lambda _1}f\left( {{{\vec x}_1}} \right) + \ldots + {\lambda _n}f\left( {{{\vec x}_n}} \right)\]
Théorème
Soient* E* et* F* deux espaces vectoriels sur \[\mathbb{R}\] et \(f\) une application de* E* dans* F*. \(f\) est une application linéaire si et seulement si :
\[\forall \vec x,\vec y \in E\], \[f\left( {\vec x + \vec y} \right) = f\left( {\vec x} \right) + f\left( {\vec y} \right)\]
\[\forall \vec x \in E\], \[\forall \lambda \in \mathbb{R}\], \[f\left( {\lambda \vec x} \right) = \lambda f\left( {\vec x} \right)\] *
Remarques
« On dira donc que \(f\) est linéaire si elle conserve les deux opérations de base d’un espace vectoriel c’est-à-dire l’addition et la multiplication par un scalaire.
« En remplaçant \[\lambda \] par 0 dans (ii), on obtient que \[f\left( {\vec 0} \right) = \vec 0\] : l’image du vecteur nul par toute application linéaire est égale au vecteur nul.
« L’ensemble des applications linéaires de* E* dans* F* est noté \[L\left( {E,F} \right)\].
Exemples
- Montrer que \[f:{\mathbb{R}^3} \to {\mathbb{R}^2}\] définie par \(\vec x = \left( {{x_1},{x_2},{x_3}} \right) \mapsto f\left( {\vec x} \right) = \left( {{x_1} - {x_2},2{x_2} + 3{x_3}} \right)\) est bien une application linéaire. Réponse.
- Soit \[{C^n}\left( {\mathbb{R},\mathbb{R}} \right)\] l’espace vectoriel des fonctions réelles d’une variable réelles continue, \(n\)-fois dérivables et à dérivées toutes continues. Montrer que l’application \[D:{C^n}\left( {\mathbb{R},\mathbb{R}} \right) \to {C^{n - 1}}\left( {\mathbb{R},\mathbb{R}} \right)\] qui à toute fonction \(f\) de \[{C^n}\left( {\mathbb{R},\mathbb{R}} \right)\] associe sa dérivée est linéaire. Réponse.
- Montrer que la translation définie \[{\mathbb{R}^2}\] dans \[{\mathbb{R}^2}\] par \[f\left( {x,y} \right) = \left( {x + 1,y + 2} \right)\] n’est pas une application linéaire. Réponse.
Définition
On appelle application identité \[I{d_E}:E \to E\], l’application telle que \[\forall \vec u \in E\], \[I{d_E}\left( {\vec u} \right) = \vec u\] ; C’est une application linéaire.
2 Image et noyau d’une application linéaire
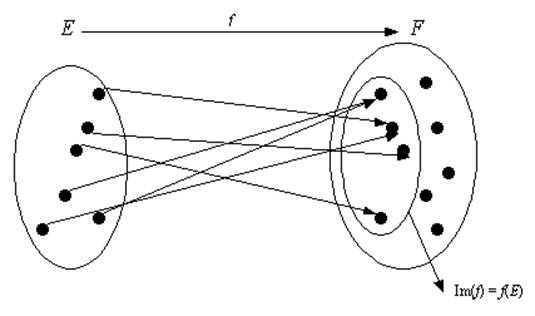
Proposition 1
Soit \(f\) :* E* ®* F* une application linéaire. L’ensemble des images des éléments de* E, \[f\left( E \right)\], est un sous-espace vectoriel de F* appelé image de l’application linéaire \(f\) et noté \[\operatorname{Im} f\].
\[\vec v \in \operatorname{Im} f \Leftrightarrow \exists \vec u \in E/\vec v = f\left( {\vec u} \right)\] *
Unnamed Image
Remarque
\[\operatorname{Im} f\]est une partie de* F* : \[\operatorname{Im} f \subseteq F\]
La dimension de \[\operatorname{Im} f\] est appelée rang de \(f\) : \[rg\left( f \right) = \dim \left( {\operatorname{Im} f} \right)\]. *
Proposition 2
Soit \(f\) :* E* ®* F* une application linéaire. Alors \[f\left( E \right) * \operatorname{Im} f\] est un espace-vectoriel. *
Proposition 3
Soit \(f\) :* E* ®* F. L’ensemble défini par \[\ker f = \left\{ {\vec u \in E/f\left( {\vec u} \right) = \vec 0} \right\}\] est un sous-espace vectoriel de E* appelé noyau de l’application linéaire \(f\). (ker = kernel qui veut dire noyau en anglais).
Remarque
\[\ker f\]* est une partie de E* : \[\ker f \subseteq E\].
Exemple 2 ( très important)
très important)
Soit \($\begin{array}{*{20}{c}}\)
- {f:}&{{^3}}& &{{^3}}$
\(\end{array}\)$ définie par :
\[\vec u = \left( {{u_1},{u_2},{u_3}} \right) \mapsto f\left( {\vec u} \right) = \left( {{u_1} + 2{u_2} - {u_3},{u_2} + {u_3},{u_1} + {u_2} - 2{u_3}} \right)\].
Déterminer \[\operatorname{Im} f\] et \[\ker f\]. Réponse.
3 Image d’une famille de vecteurs
3.1 Injectivité
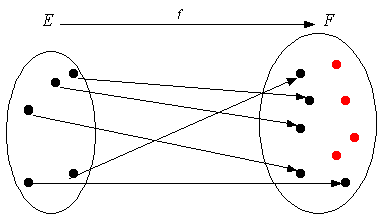
Définition 1
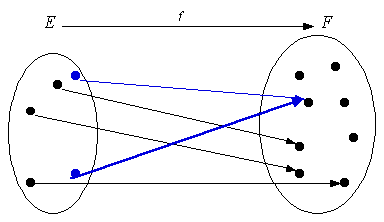
Une application \(f\) :* E* ®* F* est dite injective si des éléments distincts de* E* ont des images distinctes : \[\vec u \ne \vec u' \Rightarrow f\left( {\vec u} \right) \ne f\left( {\vec u'} \right)\] \[ \Leftrightarrow \] \[f\left( {\vec u} \right) = f\left( {\vec u'} \right) \Rightarrow \vec u = \vec u'\] (contraposition). *
Unnamed Image
OUI !
· Il peut y avoir des éléments isolés dans* F*
Unnamed Image
NON !
· Deux éléments distincts de* E* ne peuvent pas avoir la même image dans* F* *
Proposition 1
Soit \[f \in L\left( {E,F} \right)\], \(f\) est injective si et seulement si \[\ker f = \left\{ {\vec 0} \right\}\]. *
3.2 Surjectivité
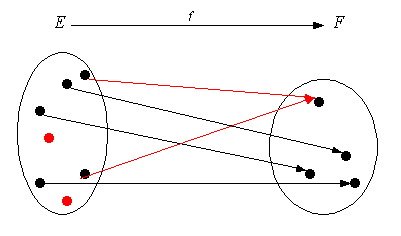
Définition 2
Soit \[f \in L\left( {E,F} \right)\], \(f\) est surjective si tout vecteur \[\vec v\] de* F* possède au moins un antécédent par \(f\) dans* E* : \[\forall \vec v \in F,\exists \vec u \in E/f\left( {\vec u} \right) = \vec v\]. *
Unnamed Image
OUI !
· Un élément de* F* peut avoir plusieurs antécédents dans* E*
· Il peut y avoir des éléments isolés dans* E*
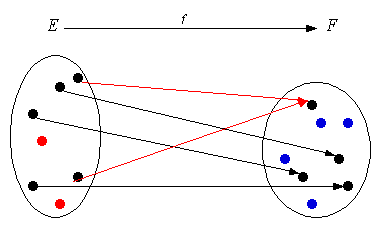
Unnamed Image
NON !
· Il ne peut y avoir d’éléments isolés dans* F*
Proposition 2
f est surjective si et seulement si \[\operatorname{Im} f = f\left( * \right) = F\]. *
3.3 Bijectivité
Proposition 3
Soit* \[f \in L\left( {E,F} \right)\], \(f\) est dite bijective si et seulement si elle est à la fois injective et surjective.
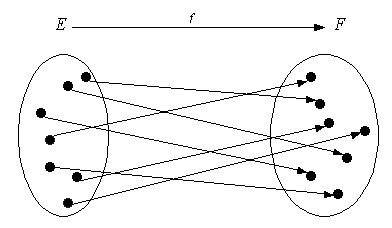
Unnamed Image
· Tout élément de* E* possède une image unique dans* F*
· Tout élément de* F* possède un antécédent unique dans* E*.
Théorème de la dimension
Soient* E* et* F* deux espaces vectoriels et \(E\) de dimension finie et soit \(f\) une application linéaire de \[L\left( {E,F} \right)\], on a alors :
\[\dim \left( E \right) * \dim \left( {\operatorname{Im} f} \right) + \dim \left( {\ker f} \right)\left[ { = {\text{rg}}\;f + \dim \left( {\ker f} \right)} \right]\]
Proposition 4
\[f \in L\left( {E,F} \right)\] bijective \[ \Rightarrow \dim \left( E \right) = \dim \left( F \right)\]. *
Remarque
La démonstration de la proposition 4 est immédiate :
\(f\) est bijective donc å injective : \[\ker f = \left\{ {\vec 0} \right\}\] (proposition 1) * å surjective : \[\operatorname{Im} f = F\] (proposition 2)
Or \[\dim \left( E \right) = \dim \left( {\operatorname{Im} f} \right) + \dim \left( {\ker f} \right) = \dim \left( F \right) + \dim \left( {\ker f} \right) = \dim \left( F \right) + 0 = \dim \left( F \right)\].
Conséquences
· Si \[\dim \left( * \right) = p\] alors \[\dim \left( {\operatorname{Im} f} \right) \leqslant p\]
· Si \[\dim \left( * \right) = p\] et si \[\dim \left( {\operatorname{Im} f} \right) = p\] alors \[\dim \left( {\ker f} \right) = 0\]
Soit \[\ker f = \left\{ {\vec 0} \right\}\] \[ \Leftrightarrow \] \(f\) est injective.
· Si \[\dim \left( * \right) = \dim \left( F \right)\], \(f\) bijective \[ \Leftrightarrow \] \(f\) injective \[ \Leftrightarrow \] \(f\) surjective. *
Définitions (voir Introduction)
« Une application linéaire \[f \in L\left( {E,E} \right)\] est appelée endomorphisme.
« Une application linéaire bijective de \[L\left( {E,F} \right)\] est appelée isomorphisme.
« Une application linéaire bijective de \[L\left( {E,E} \right)\] est un automorphisme ou endomorphisme bijectif.
Exemple
Soit \[f:{\mathbb{R}^2} \to {\mathbb{R}^2}\] définie par \[\left( {x,y} \right) \mapsto \left( {x + y,2y} \right)\]. \(f\) est-elle surjective ? bijective ? Réponse.
4 Opérations sur les applications linéaires
Proposition
\[L\left( {E,F} \right)\] muni des deux lois suivantes :
\[\forall f,g \in L\left( {E,F} \right)\], \[f + g \in L\left( {E,F} \right)\] (loi de composition interne)
\[\forall f \in L\left( {E,F} \right)\], \[\forall \lambda \in \mathbb{R}\], \[\lambda f \in L\left( {E,F} \right)\] (loi de composition externe)
est un espace vectoriel.
Définition * Proposition
Soient* E, F, G*, trois espaces vectoriels, soient \[f \in L\left( {E,F} \right)\] et \[g \in L\left( {F,G} \right)\]. On définit la composée de deux applications linéaires \(f\) et \(g\) notée \(g\)$ \[f$ comme l’application \]h L( {E,G} )\[ qui à \]u\[ Î* E* associe \]g( {f( {u} )} )$$ :
\($\begin{gathered}\)
h:EFG \$
u;f( {u} ); ;g( {f( {u} )} ) = h( {u} ) \$
$\end{gathered} $$
Remarques
- \[g \circ f\] signifie que l’on applique d’abord \(f\) puis ensuite \(g\).
- La composition n’est possible que si l’ensemble d’arrivée de \(f\) est inclus dans l’ensemble de départ de \(g\).
- Si \[g \circ f\] existe, \[f \circ g\] n’existe pas forcément.
- Si \[f \circ g\] existe, alors généralement \[g \circ f \ne f \circ g\]
Exemple 3
Soient deux applications linéaires définies par :
\($\begin{array}{*{20}{l}}\)
{f:}&{{^2}}& &{{^2}} \$
{}&{( {{u_1},{u_2}} )}& &{( {3{u_1} + {u_2},{u_1} - {u_2}} )}$
\(\end{array}\)$ \($\begin{array}{*{20}{l}}\)
{g:}&{{^2}}& &{{^2}} \$
{}&{( {{v_1},{v_2}} )}& &{( {{v_1} + 2{v_2}, - 3{v_1} + {v_2}} )}$
\(\end{array}\)$
Calculer quand c’est possible \[g \circ f\] et \[f \circ g\]. Réponse.
Remarque
Il est facile de démontrer que \[h = g \circ f\] est bien une application linéaire :
\[h\left( {\lambda \vec u + \mu \vec v} \right) = g\left( {f\left( {\lambda \vec u + \mu \vec v} \right)} \right) * g\left( {\lambda f\left( {\vec u} \right) + \mu f\left( {\vec v} \right)} \right)\] car \(f\) est linéaire.
\[h\left( {\lambda \vec u + \mu \vec v} \right) = g\left( {\lambda f\left( {\vec u} \right)} \right) + g\left( {\mu f\left( {\vec v} \right)} \right) = \lambda g\left( {f\left( {\vec u} \right)} \right) + \mu g\left( {f\left( {\vec v} \right)} \right)\] car \(g\) est linéaire.
\[h\left( {\lambda \vec u + \mu \vec v} \right) = \lambda h\left( {\vec u} \right) + \mu h\left( {\vec v} \right)\]
Théorème
\[f \circ \left( {{g_1} + {g_2}} \right) = \left( {f \circ {g_1}} \right) + \left( {f \circ {g_2}} \right)\]
\(\left( {{f_1} + {f_2}} \right) \circ g = \left( {{f_1} \circ g} \right) + \left( {{f_2} \circ g} \right)\)
\[\lambda \left( {f \circ g} \right) = \left( {\lambda f} \right) \circ g = f \circ \left( {\lambda g} \right)\]
5 Réciproque d’une application linéaire bijective
Lorsque \(f\) est bijective, tout \[\vec v\]Î* F* possède un antécédent unique \[\vec u\] par \(f\) dans* E*.
Définition
On appelle application réciproque de \(f\), notée \[{f^{ - 1}}\], l’application qui à \[\vec v\] associe \[\vec u\] ; c’est une application linéaire : \[{f^{ - 1}} \in L\left( {F,E} \right)\].
Remarque
\($\begin{array}{*{20}{l}}\)
{f:}&E& &F \$
{}&{u}& &{v = f( {u} )}$
\(\end{array}\)$ \($\begin{array}{*{20}{l}}\)
{{f^{ - 1}}:}&F& &E \$
{}&{v}& &{u = {f^{ - 1}}( {v} )}$
\(\end{array}\)$
Propriété
\[f \circ {f^{ - 1}} = I{d_F}\] et \[{f^{ - 1}} \circ f = I{d_E}\], ce qui peut aussi se traduire comme suit :
\($\begin{array}{*{20}{l}}\)
{f :}&F&{}&E&{}&F \$
{{f^{ - 1}} f:}&E&{}&F&{}&E$
\(\end{array}\)$
Exemple 4 : Déterminer l’application réciproque de f définie par
\($\begin{array}{*{20}{l}}\)
{f:}&{{^2}}& &{{^2}} \$
{}&{( {{u_1},{u_2}} )}& &{( {{v_1},{v_2}} ) = ( {2{u_1} - {u_2},{u_1}} )}$
\(\end{array}\)$ Réponse
6 Projecteurs et involutions
6.1 Projections et projecteurs
Définition 1
Soient \(F\) et \(G\) deux sous-espaces supplémentaires dans \(E\). Alors \[F \oplus G = E\] et on appelle projection sur \(F\) parallèlement à \(G\), l’endomorphisme \[{p_{F,G}}\] tel que :
\[\forall \vec x \in F\], alors \[{p_{F,G}}\left( {\vec x} \right) = \vec x\] ; Les éléments de \(F\) restent invariants par \[{p_{F,G}}\].
\[\forall \vec y \in G\], alors \[{p_{F,G}}\left( {\vec y} \right) = \vec 0\].
Définition 2
· Un endomorphisme \(f\) de \(E\) est dit idempotent lorsque \[f \circ f = f\].
· On appelle projecteur de \(E\) tout endomorphisme idempotent de \(E\).
Remarque
Toute projection \[{p_{F,G}}\] est un projecteur. *
Exemples
Montrer que l’application \[p:{\mathbb{R}^2} \to {\mathbb{R}^2}\] définie par \[\left( {x,y} \right) \mapsto \left( {x,0} \right)\] est un projecteur. Réponse.
Montrer que l’application \[p:{\mathbb{R}^2} \to {\mathbb{R}^2}\] définie par \[\left( {x,y} \right) \mapsto \left( {x,0} \right)\] est une projection sur \(F\) parallèlement à \(G\). Identifier \(F\) et \(G\). Réponse.
Proposition
Soit \(p\) un projecteur de \(E\). Alors \($\operatorname{Im} p = \left\{ {{{\vec x \in E} \mathord{\left/\)
\({\vphantom {{\vec x \in E} {p\left( {\vec x} \right) * \vec x}}} \right.\)
\(\kern-\nulldelimiterspace} {p\left( {\vec x} \right) * \vec x}}} \right\}\)$. \[\operatorname{Im} p\] est l’ensemble de tous les éléments de \(E\) invariant par \(p\).
Démonstration
Soit \[\vec x \in \operatorname{Im} p\]. Alors \[\exists \vec y \in E\] tel que \[\vec x = p\left( {\vec y} \right)\]. Ainsi \[p\left( {\vec x} \right) = \left( {p \circ p} \right)\left( {\vec y} \right) = p\left( {\vec y} \right) = \vec x\].
De même si \[p\left( {\vec x} \right) = \vec x\], alors \[\vec x \in \operatorname{Im} p\], d’où l’égalité.
Propriétés
Soit p un projecteur de E. Alors \[\ker p \oplus \operatorname{Im} p = E\].
Si p est un projecteur de E, alors nécessairement p est la projection sur \[\operatorname{Im} p\] parallèlement à \[\ker p\].
Soit p un endomorphisme de E. \[I{d_E} - p\], avec \[I{d_E}\] l’application identité de E, est un projecteur si et seulement si p est un projecteur.
Si p est un projecteur de E, alors \[\ker \left( {I{d_E} - p} \right) = \operatorname{Im} p\] et \[\operatorname{Im} \left( {I{d_E} - p} \right) = \ker p\].
Définition
Si \(p\) est un projecteur de \(E\), alors on dit que \(p\) et \[I{d_E} - p\] sont des projecteurs associés.
6.2 Symétries et involutions
Définition 1
Soient \(F\) et \(G\) deux sous-espaces supplémentaires dans \(E\). Alors \[F \oplus G = E\] et on appelle symétrie par rapport à \(F\) parallèlement à \(G\), l’endomorphisme \[{s_{F,G}}\] tel que :
\[\forall \vec x \in F\], alors \[{s_{F,G}}\left( {\vec x} \right) = \vec x\] ; Les éléments de \(F\) restent invariants par \[{s_{F,G}}\].
\[\forall \vec y \in G\], alors \[{s_{F,G}}\left( {\vec y} \right) = - \vec y\] ; Les éléments de \(G\) sont changés en leur opposé par \[{s_{F,G}}\].
Définition 2
Un endomorphisme \(s\) de \(E\) est une involution linéaire lorsque \[s \circ s = I{d_E}\].
Remarque
Toute symétrie \[{s_{F,G}}\] est une involution linéaire.
Exemples
Montrer que l’application \[s:{\mathbb{R}^2} \to {\mathbb{R}^2}\] telle que \[\left( {x,y} \right) \mapsto \left( {x, - y} \right)\] est une involution linéaire. Réponse.
Montrer que l’application \[s:{\mathbb{R}^2} \to {\mathbb{R}^2}\] définie par \[\left( {x,y} \right) \mapsto \left( {x, - y} \right)\] est une symétrie sur \(F\) parallèlement à \(G\). Identifier \(F\) et \(G\). Réponse.
Propriété
Soient F et G deux sous-espaces supplémentaires dans E. Les endomorphismes \[{s_{F,G}}\] et \[{p_{F,G}}\] sont liés par la relation \[{s_{F,G}} = 2{p_{F,G}} - I{d_E}\].