Chapitre 1 — Espaces vectoriels
Sandrine CHARLES : scharles@biomserv.univ-lyon1.fr
Introduction
L’algèbre linéaire est un champ mathématique utilisé dans pratiquement toutes les branches scientifiques. En effet, beaucoup de problèmes vérifient la propriété suivante : si \(u\) et \(v\) sont deux solutions alors \[u + v\] est aussi une solution, ainsi que \[k \times u\] si \(k\) est un nombre réel ou complexe. De tels problèmes sont dits linéaires et sont plus faciles à résoudre que certains problèmes généraux.
Un premier exemple
Si on considère deux points dans un plan, la droite qui les relie définit une direction, et une flèche sur cette droite définit un sens. * align=center>
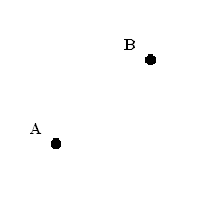
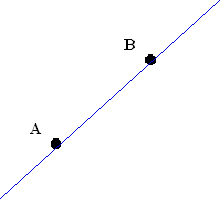
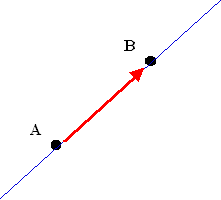
Deux points
une direction
un sens
Deux points avec une direction et un sens forment un vecteur du plan noté \[\overrightarrow {AB} \].
Sur des vecteurs de même origine, on peut définir deux opérations (cohérentes avec ce que vous avez vu des forces en physique) :
- L’addition : Règle du parallélogramme
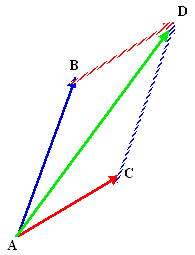
$ + = $
- Le produit d’un vecteur par un nombre. On obtient un vecteur de même direction et de « longueur » multipliée par \[\left| \lambda \right|\]. Le signe de \[\lambda \] peut alors modifier le « sens » du vecteur résultat :
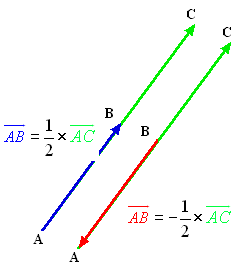
Un deuxième exemple
L’expression \[{a_0} + {a_1}x * {a_2}{x^2} + \ldots + {a_n}{x^n}\], dont les coefficients \[{a_0},{a_1},{a_2}, \ldots ,{a_n}\] appartenant à \[\mathbb{R}\], est un polynôme de degré \(n\). On peut comme précédemment définir deux opérations sur les polynômes :
- L’addition :
\(\begin{gathered}\)
{}( x ) * {a_0} + {a_1}x + {a_2}{x^2} + + {a_n}{x^n} \$
{}( x ) * {b_0} + {b_1}x + {b_2}{x^2} + + {b_n}{x^n} \$
( {{}} )( x ) = ( {{a_0} + {b_0}} ) + ( {{a_1} + {b_1}} )x + ( {{a_2} + {b_2}} ){x^2} + + ( {{a_n} + {b_n}} ){x^n} \$
$\end{gathered} $
Le polynôme \[{\text{P + Q}}\] est également un polynôme de degré \(n\).
- Le produit d’un polynôme par un nombre \[\lambda \in \mathbb{R}\]. On obtient un polynôme dont tous les coefficients sont multipliés par \[\lambda \] :
\(\begin{gathered}\)
{}( x ) * {a_0} + {a_1}x + {a_2}{x^2} + + {a_n}{x^n} \$
( {} )( x ) = ( {} ) + ( {} )x + ( {} ){x^2} * + ( {} ){x^n} \$
$\end{gathered} $
Le polynôme \[\lambda \times {\text{P}}\] est également un polynôme de degré \(n\).
Il est petit à petit apparu que de tels ensembles (l’ensemble des vecteurs, l’ensemble des polynômes de degré \(n\), et bien d’autres encore), pourtant très différents les uns des autres, se ressemblent en fait au travers de l’existence de deux opérations : l’addition (+) et le produit par un nombre réel (\[ \times \]). Pour permettre de ne pas répéter à chaque fois les caractéristiques et propriétés de ces ensembles, les mathématiciens ont défini un « modèle » qui ne vérifie qu’un nombre minimum de propriétés (des axiomes), mais juste assez pour éviter des cas pathologiques. Ce modèle, encore appelé Espace Vectoriel, a donc des propriétés partagées par de nombreux ensembles, comme celui des vecteurs, celui des polynômes de degré \(n\), et bien d’autres encore que nous rencontrerons dans ce cours.
Historiquement, c’est à Peano que revient le mérite d’avoir défini de façon axiomatique le concept d’espace vectoriel sur un corps de scalaires. Le terme scalaires (du latin scalaris = escalier, échelle) est utilisé au sens de numérique.